人教版数学八年级下册16.2 二次根式的乘除第2课时 课件(31张ppt)
文档属性
| 名称 | 人教版数学八年级下册16.2 二次根式的乘除第2课时 课件(31张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-19 13:42:12 | ||
图片预览






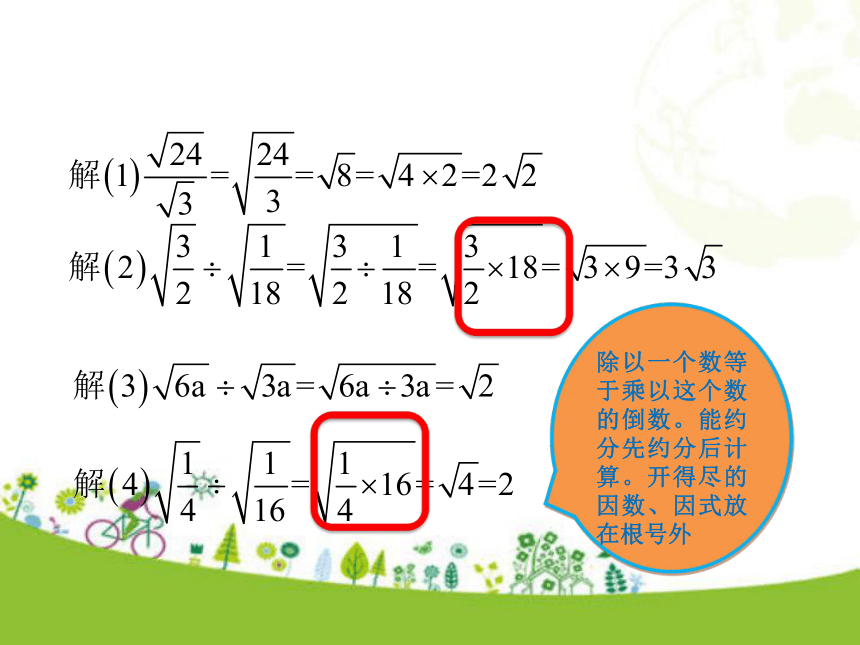

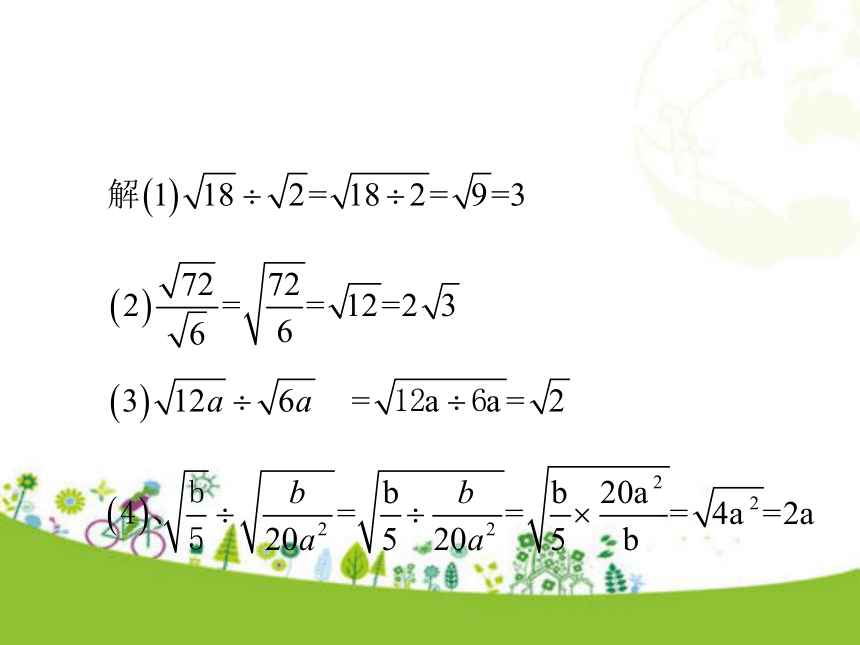

文档简介
课件31张PPT。16.2 二次根式的乘除第2课时人教版数学八年级下册1、知识与技能:
理解 (a≥0,b>0)和 (a≥0,b>0)及利用它们进行运算.
理解最简二次根式的概念,并运用它把不是最简二次根式的化成最简二次根式.
学习目标2、过程与方法 :
通过学生练习活动,发现规律,由特殊运算归纳出一般的除法法则,并用逆向思维写出逆向等式及利用它们进行计算和化简.分析计算或化简的结果提炼最简二次根式的概念,并根据它的特点来检验最后结果是否满足最简二次根式的要求.
3、情感态度与价值观 :
发挥学生的主体作用,增强学生学数学、用数学的兴趣,创设探究式与合作交流的的学习气氛
(学生活动)请同学们完成下列问题:
写出二次根式的乘法法则及逆运算等式.
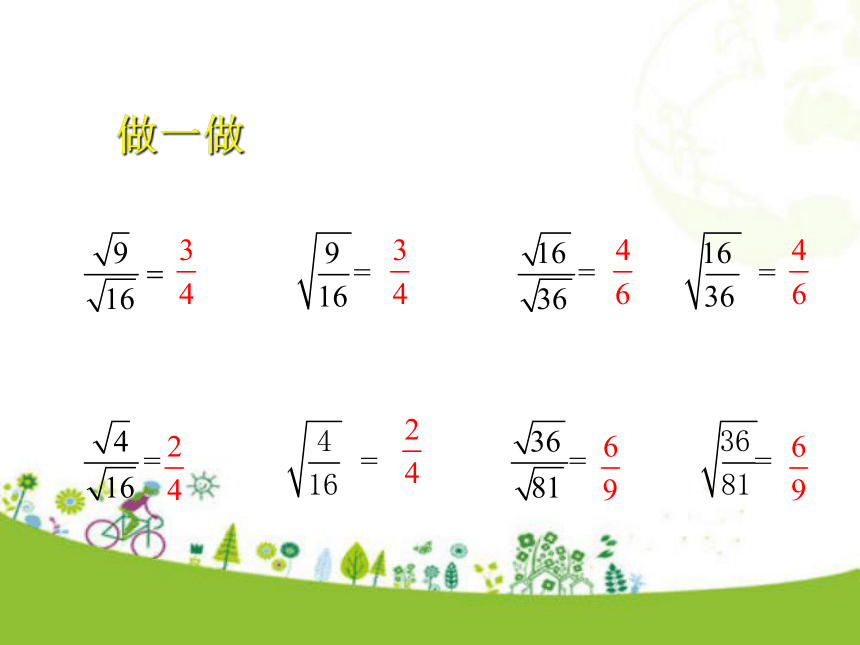
那么二次根式除法运算有什么规律呢?请观察下列各式计算结果:新课导入做一做
观察以上运算我们发现:
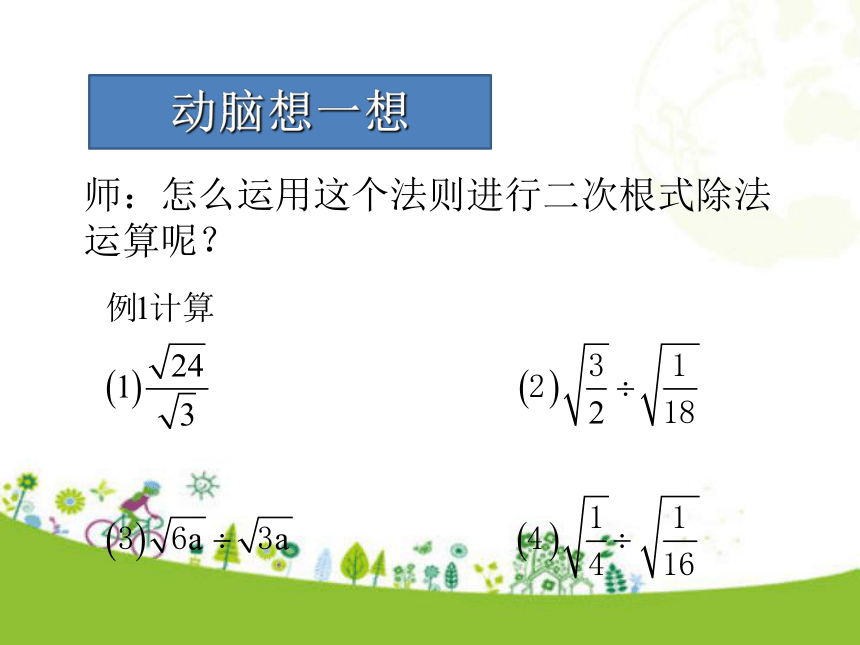
知识讲解二次根式的除法知识点1 除法法则即两个非负数的算术平方根的商等于这两数商的算术平方根。由此可得二次根式的除法法则:动脑想一想师:怎么运用这个法则进行二次根式除法运算呢?除以一个数等于乘以这个数的倒数。能约分先约分后计算。开得尽的因数、因式放在根号外师:同学们学会了吗?请大家小试身手。
巩固训练1二次根式除法法则的逆运用知识点2巩固训练2化简时要注意1、运算符号。2、运用公式。3、约分与开方兼顾学生小组合作展示学习成果教师点评 结果:分母中不含根式 分享硕果整式与整式结合,根式与根式结合 再接再厉变式目的:去掉分母中根号再接再厉二次根式的运算结果有以下特点:
(1)被开方数不含分母;
(2)被开方数中不含能开得尽方的因数或因式. 我们把满足上述两个条件的二次根式,叫做最简二次根式.最简二次根式即被开方数必须是整数(式)知识点3现在来看本章引言:可得它们的半径之比是 怎样把这个式子化简呢?由此可得传播半径比只与高度有关例3把下列各式化成最简二次根式回顾最简二次根式的条件化简。
1.被开方数不含分母;
2.被开方数中不含能开得尽方的因数或因式.小数化成分数再去掉分母中根号巩固训练(-b)2=b21.如果等式 成立,那么( )
A.x≥0 B.x>3 C.x≠3 D.x≥3B2.下列各式中,是最简二次根式的是( )C随堂练习最简二次根式条件:
1.被开方数不含分母;
2.被开方数中不含能开得尽方的因数或因式.二次根式的除法法则课堂小结谢谢!
理解 (a≥0,b>0)和 (a≥0,b>0)及利用它们进行运算.
理解最简二次根式的概念,并运用它把不是最简二次根式的化成最简二次根式.
学习目标2、过程与方法 :
通过学生练习活动,发现规律,由特殊运算归纳出一般的除法法则,并用逆向思维写出逆向等式及利用它们进行计算和化简.分析计算或化简的结果提炼最简二次根式的概念,并根据它的特点来检验最后结果是否满足最简二次根式的要求.
3、情感态度与价值观 :
发挥学生的主体作用,增强学生学数学、用数学的兴趣,创设探究式与合作交流的的学习气氛
(学生活动)请同学们完成下列问题:
写出二次根式的乘法法则及逆运算等式.
那么二次根式除法运算有什么规律呢?请观察下列各式计算结果:新课导入做一做
观察以上运算我们发现:
知识讲解二次根式的除法知识点1 除法法则即两个非负数的算术平方根的商等于这两数商的算术平方根。由此可得二次根式的除法法则:动脑想一想师:怎么运用这个法则进行二次根式除法运算呢?除以一个数等于乘以这个数的倒数。能约分先约分后计算。开得尽的因数、因式放在根号外师:同学们学会了吗?请大家小试身手。
巩固训练1二次根式除法法则的逆运用知识点2巩固训练2化简时要注意1、运算符号。2、运用公式。3、约分与开方兼顾学生小组合作展示学习成果教师点评 结果:分母中不含根式 分享硕果整式与整式结合,根式与根式结合 再接再厉变式目的:去掉分母中根号再接再厉二次根式的运算结果有以下特点:
(1)被开方数不含分母;
(2)被开方数中不含能开得尽方的因数或因式. 我们把满足上述两个条件的二次根式,叫做最简二次根式.最简二次根式即被开方数必须是整数(式)知识点3现在来看本章引言:可得它们的半径之比是 怎样把这个式子化简呢?由此可得传播半径比只与高度有关例3把下列各式化成最简二次根式回顾最简二次根式的条件化简。
1.被开方数不含分母;
2.被开方数中不含能开得尽方的因数或因式.小数化成分数再去掉分母中根号巩固训练(-b)2=b21.如果等式 成立,那么( )
A.x≥0 B.x>3 C.x≠3 D.x≥3B2.下列各式中,是最简二次根式的是( )C随堂练习最简二次根式条件:
1.被开方数不含分母;
2.被开方数中不含能开得尽方的因数或因式.二次根式的除法法则课堂小结谢谢!
