2020春华师大版九下数学27.1.1圆的基本元素教学课件(23张)
文档属性
| 名称 | 2020春华师大版九下数学27.1.1圆的基本元素教学课件(23张) |

|
|
| 格式 | zip | ||
| 文件大小 | 517.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-19 00:00:00 | ||
图片预览





文档简介
课件23张PPT。
华师九年级数学下册第27章《圆》1.圆的认识27.1.1圆的基本元素50%20%30%步行公共汽车其他那么,如何确定一个圆呢?知识回顾一一、圆的定义:
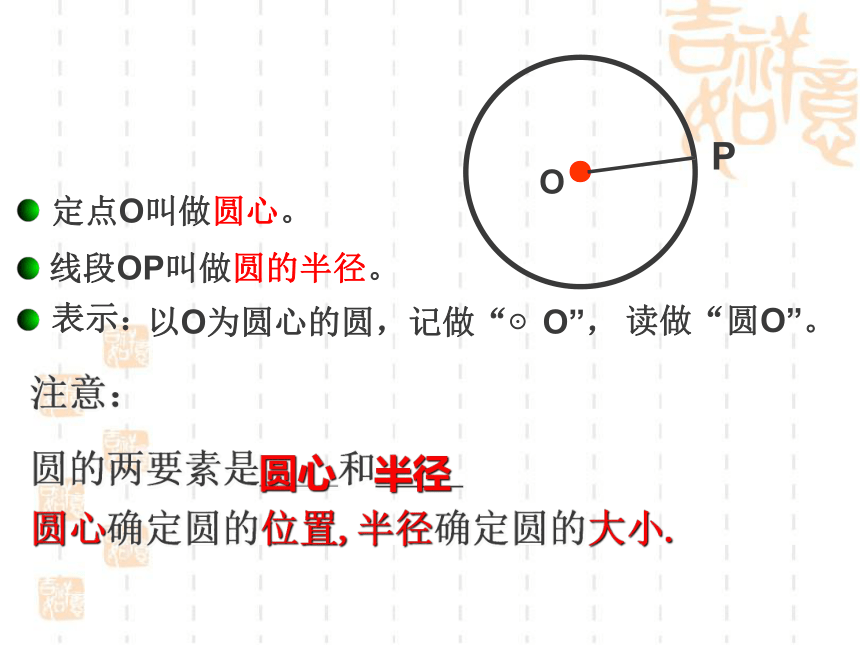
在同一平面内,线段OP绕它固定的一个端点O旋转一周,另一端点P运动所形成的图形叫做圆。注意这里所指的圆是指圆周。
而不是一个圆的平面注意:
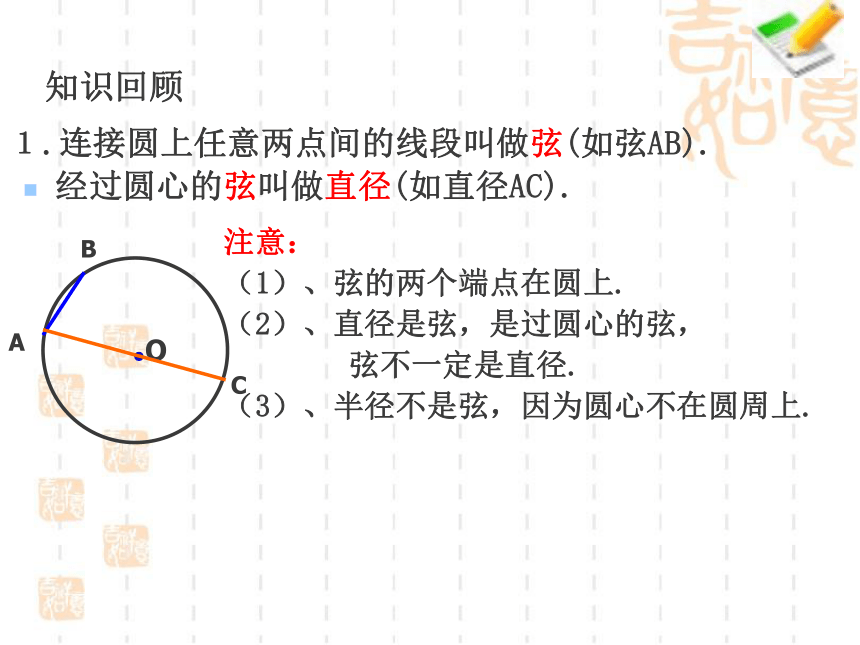
圆的两要素是____和____圆心半径圆心确定圆的位置,半径确定圆的大小.知识回顾1.连接圆上任意两点间的线段叫做弦(如弦AB).经过圆心的弦叫做直径(如直径AC).AB注意:
(1)、弦的两个端点在圆上.
(2)、直径是弦,是过圆心的弦,
弦不一定是直径.
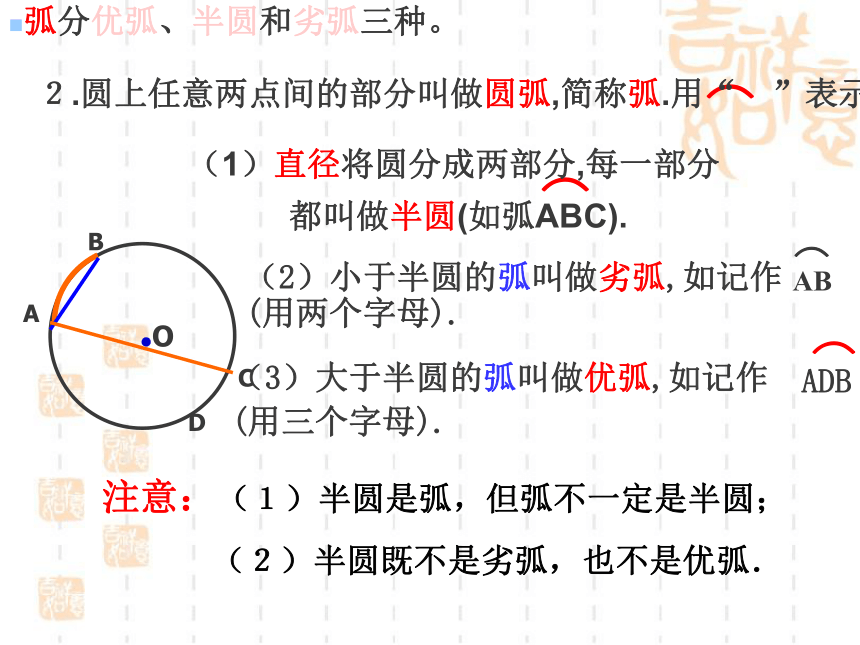
(3)、半径不是弦,因为圆心不在圆周上.弧分优弧、半圆和劣弧三种。AB⌒⌒注意:(1)半圆是弧,但弧不一定是半圆;
(2)半圆既不是劣弧,也不是优弧.
2.圆上任意两点间的部分叫做圆弧,简称弧.用“ ”表示(1)直径将圆分成两部分,每一部分
都叫做半圆(如弧ABC).3.圆心角:
顶点在圆心的角叫做圆心角。
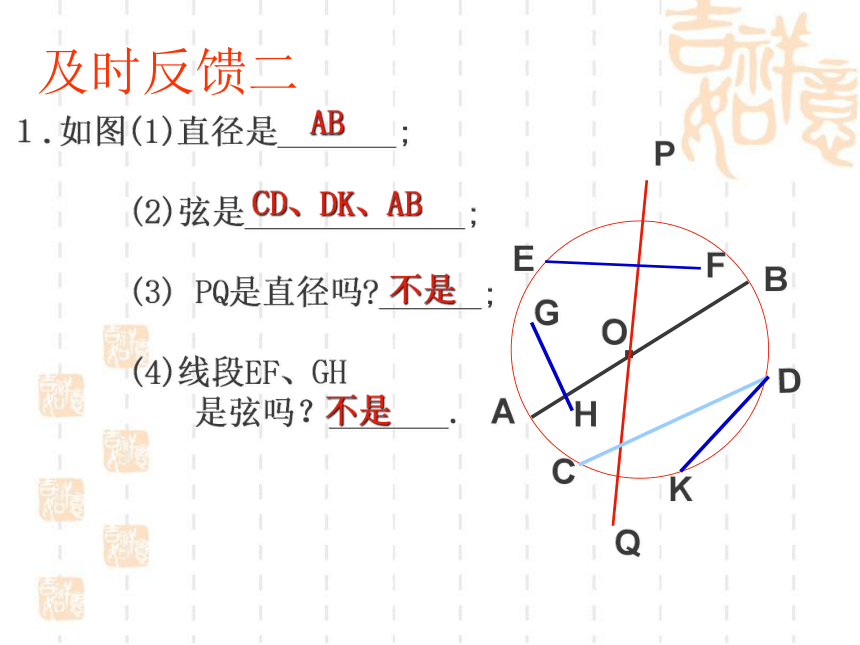
∠AOB、∠AOC、∠BOC就是圆心角。 4.同心圆 5.等圆同圆或等圆的半径相等。圆心相同,半径不同的两圆半径相同,能够互相重合的两个圆注意:在大小不等的两个圆中,不存在等弧。 6.在同圆或等圆中,能够互相重合的弧叫等弧。.OADQCBPHGFE1.如图(1)直径是_______;
(2)弦是_____________;
(3) PQ是直径吗?______;
(4)线段EF、GH
是弦吗?_______.KABCD、DK、AB不是不是及时反馈二O在圆中有长度不等的弦。直径是圆中最长的弦。你会证明吗?如图,任作一条弦(非直径)连结OC,OD证明:∵在⊿OCD中,两边之和大于第三边∴0C+OD>CD又∵ 0C+OD=2r=d∴d>CD
即直径是圆中最长的弦2.∠CMB, ∠CMA是不是圆心角?圆心角有:∠DOE , ∠COE
不是强调:圆心角的顶点必须在圆心 3.如图 劣弧有:优弧有:注意:和角一样,优弧的三个字母也是有顺序的。 (2)请任选一条弦,写出这条弦所对的弧.注意:一条弦对的弧有两条14434(1)如图,有____条直径,____条弦,
以A为一个端点的优弧有___个,劣弧有___个5.判断
(1)长度相等的两条弧是等弧。
(2)圆的任何一条弦的两端点,把圆分成两条弧,所以一条弦对两条弧。
(3)面积相等的两个圆是等圆。
(4)直径是弦,且圆内最长的弦是直径。
(5)半圆是弧,弧小于半圆。××例2.如图,E是⊙O上一点,AB是⊙O的弦,OE的延长线交AB的延长线于C。如果BC=OE, ∠C=40°,求∠ EOA的度数。分析: BC=OE,就是告诉我们BC等于圆的半径解:连结OB
∵ BC=OE∴BC=OB∴∠C=∠BOE=40°∴∠ABO= ∠C+∠BOE=80°又∵0A=OB∴∠A=∠ABOE= 80°∴∠ EOA=180°- 80°- 40°
= 60°
例3.如图,⊙O的半径OA、OB分别交弦CD于点E、F,且CE=DF.
求证:△OEF是等腰三角形. 方法小结:在圆中常添作的辅助线为圆的半径,构造等腰三角形或全等三角形。分析:连接OC、OD,则∠C=∠D
再用三角形全等来证明OE=OF2.下列说法:①直径是弦 ②弦是直径 ③半圆是弧,但弧不一定是半圆 ④长度相等的两条弧是等弧⑤完全重合的两条弧是等弧。
正确的命题有( )
A、1个 B、2个 C、3个 D、4个BC1、下列说法错误的是( )A、圆上的点到圆心的距离相等
B、过圆心的线段是直径
C、直径是圆中最长的弦
D、半径相等的圆是等圆及时反馈三3.如图,已知AB是⊙O的直径,AC为弦,OD∥BC,交AC于D,BC=6cm,求OD的长。分析:由OD∥BC易证⊿ADO~ ⊿ACB得相似比为1:2,所以0D=3CM4.如图,已知AB、AC是⊙O的两条弦,
且AB=AC,若∠BOC=110 °,求∠BAO的度数。分析:由 AB=AC,AO=AO,OB=OC易证⊿AOB≌ ⊿AOC∴∠AOB= ∠AOC=(360-110)÷2=125 °又∵OA=OB∴∠B= ∠BAO∴ ∠BAO= 22.5 °想想,你还有别的方法吗? 1.已知:如图,BD、CE是⊿ABC的高,M是BC的中点。试问:点B、C、D、E在以点M为圆心的圆上吗?点评:将点与圆的位置关系与直角三角形结合起来。能力提高11.过圆上一点可以作圆的最长弦有( )条.
A. 1 B. 2 C. 3 D.无数条
2.一点和⊙O上的最近点距离为4cm,最远距离为10cm,
则这个圆的半径是______cm.
3.图中有____条直径,____条非直径的弦,圆中以A为一个
端点的优弧有____条,劣弧有____条.
4.如图, ⊙O中,点A、O、D以及点B、O、C分别在一直线
上,图中弦的条数为_____。
5.CD为⊙O的直径,∠EOD=72°,AE交⊙O于B,
且AB=OC,则∠A=_______.A7或312442第5题24°及时反馈四3.理解圆的有关概念;(如弦、弧、圆心角、同心圆、等圆等);2.经历探索点与圆的位置关系的过程,会运用点到圆心的距离与圆的半径之间的数量关系判断点与圆的位置关系;1.理解圆的描述定义、集合定义;
4.在圆中常添作的辅助线为圆的半径,构造等腰三角形或全等三角形. (方法小结)小结 作业习题27.1
华师九年级数学下册第27章《圆》1.圆的认识27.1.1圆的基本元素50%20%30%步行公共汽车其他那么,如何确定一个圆呢?知识回顾一一、圆的定义:
在同一平面内,线段OP绕它固定的一个端点O旋转一周,另一端点P运动所形成的图形叫做圆。注意这里所指的圆是指圆周。
而不是一个圆的平面注意:
圆的两要素是____和____圆心半径圆心确定圆的位置,半径确定圆的大小.知识回顾1.连接圆上任意两点间的线段叫做弦(如弦AB).经过圆心的弦叫做直径(如直径AC).AB注意:
(1)、弦的两个端点在圆上.
(2)、直径是弦,是过圆心的弦,
弦不一定是直径.
(3)、半径不是弦,因为圆心不在圆周上.弧分优弧、半圆和劣弧三种。AB⌒⌒注意:(1)半圆是弧,但弧不一定是半圆;
(2)半圆既不是劣弧,也不是优弧.
2.圆上任意两点间的部分叫做圆弧,简称弧.用“ ”表示(1)直径将圆分成两部分,每一部分
都叫做半圆(如弧ABC).3.圆心角:
顶点在圆心的角叫做圆心角。
∠AOB、∠AOC、∠BOC就是圆心角。 4.同心圆 5.等圆同圆或等圆的半径相等。圆心相同,半径不同的两圆半径相同,能够互相重合的两个圆注意:在大小不等的两个圆中,不存在等弧。 6.在同圆或等圆中,能够互相重合的弧叫等弧。.OADQCBPHGFE1.如图(1)直径是_______;
(2)弦是_____________;
(3) PQ是直径吗?______;
(4)线段EF、GH
是弦吗?_______.KABCD、DK、AB不是不是及时反馈二O在圆中有长度不等的弦。直径是圆中最长的弦。你会证明吗?如图,任作一条弦(非直径)连结OC,OD证明:∵在⊿OCD中,两边之和大于第三边∴0C+OD>CD又∵ 0C+OD=2r=d∴d>CD
即直径是圆中最长的弦2.∠CMB, ∠CMA是不是圆心角?圆心角有:∠DOE , ∠COE
不是强调:圆心角的顶点必须在圆心 3.如图 劣弧有:优弧有:注意:和角一样,优弧的三个字母也是有顺序的。 (2)请任选一条弦,写出这条弦所对的弧.注意:一条弦对的弧有两条14434(1)如图,有____条直径,____条弦,
以A为一个端点的优弧有___个,劣弧有___个5.判断
(1)长度相等的两条弧是等弧。
(2)圆的任何一条弦的两端点,把圆分成两条弧,所以一条弦对两条弧。
(3)面积相等的两个圆是等圆。
(4)直径是弦,且圆内最长的弦是直径。
(5)半圆是弧,弧小于半圆。××例2.如图,E是⊙O上一点,AB是⊙O的弦,OE的延长线交AB的延长线于C。如果BC=OE, ∠C=40°,求∠ EOA的度数。分析: BC=OE,就是告诉我们BC等于圆的半径解:连结OB
∵ BC=OE∴BC=OB∴∠C=∠BOE=40°∴∠ABO= ∠C+∠BOE=80°又∵0A=OB∴∠A=∠ABOE= 80°∴∠ EOA=180°- 80°- 40°
= 60°
例3.如图,⊙O的半径OA、OB分别交弦CD于点E、F,且CE=DF.
求证:△OEF是等腰三角形. 方法小结:在圆中常添作的辅助线为圆的半径,构造等腰三角形或全等三角形。分析:连接OC、OD,则∠C=∠D
再用三角形全等来证明OE=OF2.下列说法:①直径是弦 ②弦是直径 ③半圆是弧,但弧不一定是半圆 ④长度相等的两条弧是等弧⑤完全重合的两条弧是等弧。
正确的命题有( )
A、1个 B、2个 C、3个 D、4个BC1、下列说法错误的是( )A、圆上的点到圆心的距离相等
B、过圆心的线段是直径
C、直径是圆中最长的弦
D、半径相等的圆是等圆及时反馈三3.如图,已知AB是⊙O的直径,AC为弦,OD∥BC,交AC于D,BC=6cm,求OD的长。分析:由OD∥BC易证⊿ADO~ ⊿ACB得相似比为1:2,所以0D=3CM4.如图,已知AB、AC是⊙O的两条弦,
且AB=AC,若∠BOC=110 °,求∠BAO的度数。分析:由 AB=AC,AO=AO,OB=OC易证⊿AOB≌ ⊿AOC∴∠AOB= ∠AOC=(360-110)÷2=125 °又∵OA=OB∴∠B= ∠BAO∴ ∠BAO= 22.5 °想想,你还有别的方法吗? 1.已知:如图,BD、CE是⊿ABC的高,M是BC的中点。试问:点B、C、D、E在以点M为圆心的圆上吗?点评:将点与圆的位置关系与直角三角形结合起来。能力提高11.过圆上一点可以作圆的最长弦有( )条.
A. 1 B. 2 C. 3 D.无数条
2.一点和⊙O上的最近点距离为4cm,最远距离为10cm,
则这个圆的半径是______cm.
3.图中有____条直径,____条非直径的弦,圆中以A为一个
端点的优弧有____条,劣弧有____条.
4.如图, ⊙O中,点A、O、D以及点B、O、C分别在一直线
上,图中弦的条数为_____。
5.CD为⊙O的直径,∠EOD=72°,AE交⊙O于B,
且AB=OC,则∠A=_______.A7或312442第5题24°及时反馈四3.理解圆的有关概念;(如弦、弧、圆心角、同心圆、等圆等);2.经历探索点与圆的位置关系的过程,会运用点到圆心的距离与圆的半径之间的数量关系判断点与圆的位置关系;1.理解圆的描述定义、集合定义;
4.在圆中常添作的辅助线为圆的半径,构造等腰三角形或全等三角形. (方法小结)小结 作业习题27.1
