2020春华师大版九下数学27.2.3切线的判定与性质教学课件(第1课时 15张)
文档属性
| 名称 | 2020春华师大版九下数学27.2.3切线的判定与性质教学课件(第1课时 15张) |  | |
| 格式 | zip | ||
| 文件大小 | 370.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-19 15:39:20 | ||
图片预览





文档简介
课件15张PPT。华师大版数学九年级下册27.2.3 切线 当你在下雨天快速转动雨伞时,水珠是沿着什么方向飞出的?
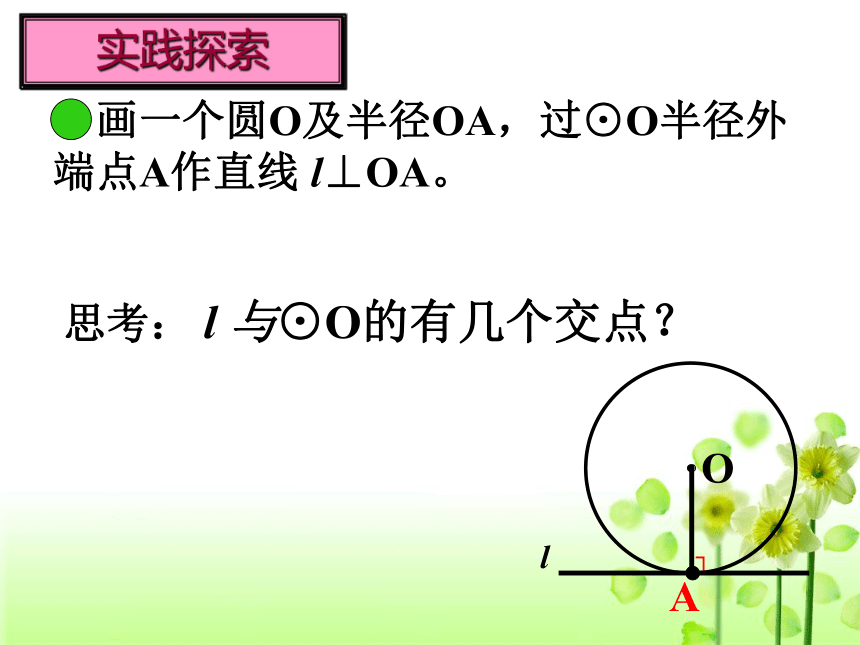
用数学的眼光看生活 画一个圆O及半径OA,过⊙O半径外端点A作直线 l⊥OA。l实践探索思考: l 与⊙O的有几个交点?┐
(1)直线 l经过半径OA的外端点A;
(2)直线l垂直于半径0A.发现总结则直线l与⊙O相切直线与圆相切的判定定理: 经过半径的外端并且垂直于这条半径的直线是圆的切线。 对定理的理解:切线需满足两条:
①经过半径外端;
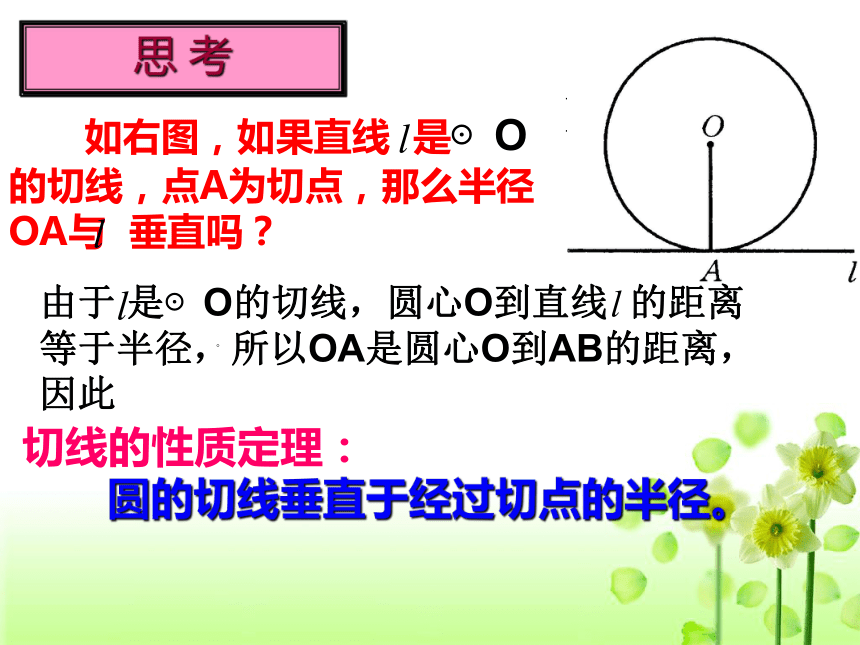
②垂直于这条半径. 画切线的方法BC经过半径的外端并且垂直于这条半径的直线是圆的切线。切线的判定定理:0。切线的性质定理:
圆的切线垂直于经过切点的半径。 思 考由于 是⊙O的切线,圆心O到直线 的距离等于半径,所以OA是圆心O到AB的距离,因此例1: 如图,直线AB经过⊙O上的点A,且AB=AO,∠OBA=45°,直线AB是⊙O的切线吗?为什么?解:直线AB是⊙O的切线。理由:∵AB=AO,∠OBA=45∴∠AOB=∠OBA=45即OA⊥AB∵点A在圆上∴直线AB是⊙O的切线。°°〖思考1〗已知:直线AB经过⊙O上的点C,并且OA=OB,CA=CB。
求证:直线AB是⊙O的切线。OBAC证明:连结OC
∵ OA=OB , CA=CB
∴ AB⊥OC
又∵ 点C在⊙O上
∴ AB是⊙O的切线〖思考2〗已知:O为∠BAC平分线上一点,OD⊥AB于D,以O为圆心,OD为半径作⊙O。
求证:⊙O与AC相切。OABCD证明:过O作OE⊥AC于E
∵ AO平分∠BAC,OD⊥AB
∴ OE=OD
又∵OD是⊙O的半径
∴ AC是⊙O切线。辅助线:作OE⊥BC于E “无切点,作垂直,证半径” 辅助线:连结OC “有切点,连半径,证垂直” 思考1、如图已知直线AB过⊙O上的点C,并且OA=OB,CA=CB
求证:直线AB是⊙O的切线思考2、如图:点O为∠ABC平分线上一点,OD⊥AB于D,以O为圆心,OD为半径作圆 求证:BC与作⊙O相切。∟O2、填空:如图AB是⊙O的直径∠ABT=45° AT=AB则AT与⊙O的位置关系是________ 1、选择:下列直线能判定为圆的切线是( )
A、与圆有公共点的直线
B、垂直于圆的半径的直线
C、到圆心的距离等于该圆半径的直线
D、过圆的半径外端的直线练习C相切o3、如图,⊙O的半径为3,P是CB延长线上一点,PO=5,PA切⊙O于点A,则PA= ________ .
练习4 1.切线的判定方法(三种): (1) 切线的定义:与圆只有一个公共点的直线, 是圆的切线; (2)圆心到直线的距离等于半径的直线,是圆的切线;* (3) 经过半径的外端且垂直于这条半径的直线是圆的切线. 2.切线的性质定理: 圆的切线垂直于经过切 点的半径小 结书本52页,1、2、3、4题 作 业
用数学的眼光看生活 画一个圆O及半径OA,过⊙O半径外端点A作直线 l⊥OA。l实践探索思考: l 与⊙O的有几个交点?┐
(1)直线 l经过半径OA的外端点A;
(2)直线l垂直于半径0A.发现总结则直线l与⊙O相切直线与圆相切的判定定理: 经过半径的外端并且垂直于这条半径的直线是圆的切线。 对定理的理解:切线需满足两条:
①经过半径外端;
②垂直于这条半径. 画切线的方法BC经过半径的外端并且垂直于这条半径的直线是圆的切线。切线的判定定理:0。切线的性质定理:
圆的切线垂直于经过切点的半径。 思 考由于 是⊙O的切线,圆心O到直线 的距离等于半径,所以OA是圆心O到AB的距离,因此例1: 如图,直线AB经过⊙O上的点A,且AB=AO,∠OBA=45°,直线AB是⊙O的切线吗?为什么?解:直线AB是⊙O的切线。理由:∵AB=AO,∠OBA=45∴∠AOB=∠OBA=45即OA⊥AB∵点A在圆上∴直线AB是⊙O的切线。°°〖思考1〗已知:直线AB经过⊙O上的点C,并且OA=OB,CA=CB。
求证:直线AB是⊙O的切线。OBAC证明:连结OC
∵ OA=OB , CA=CB
∴ AB⊥OC
又∵ 点C在⊙O上
∴ AB是⊙O的切线〖思考2〗已知:O为∠BAC平分线上一点,OD⊥AB于D,以O为圆心,OD为半径作⊙O。
求证:⊙O与AC相切。OABCD证明:过O作OE⊥AC于E
∵ AO平分∠BAC,OD⊥AB
∴ OE=OD
又∵OD是⊙O的半径
∴ AC是⊙O切线。辅助线:作OE⊥BC于E “无切点,作垂直,证半径” 辅助线:连结OC “有切点,连半径,证垂直” 思考1、如图已知直线AB过⊙O上的点C,并且OA=OB,CA=CB
求证:直线AB是⊙O的切线思考2、如图:点O为∠ABC平分线上一点,OD⊥AB于D,以O为圆心,OD为半径作圆 求证:BC与作⊙O相切。∟O2、填空:如图AB是⊙O的直径∠ABT=45° AT=AB则AT与⊙O的位置关系是________ 1、选择:下列直线能判定为圆的切线是( )
A、与圆有公共点的直线
B、垂直于圆的半径的直线
C、到圆心的距离等于该圆半径的直线
D、过圆的半径外端的直线练习C相切o3、如图,⊙O的半径为3,P是CB延长线上一点,PO=5,PA切⊙O于点A,则PA= ________ .
练习4 1.切线的判定方法(三种): (1) 切线的定义:与圆只有一个公共点的直线, 是圆的切线; (2)圆心到直线的距离等于半径的直线,是圆的切线;* (3) 经过半径的外端且垂直于这条半径的直线是圆的切线. 2.切线的性质定理: 圆的切线垂直于经过切 点的半径小 结书本52页,1、2、3、4题 作 业
