鲁教版(五四制) 八年级下册 第七章 二次根式 复习课件(43张PPT)
文档属性
| 名称 | 鲁教版(五四制) 八年级下册 第七章 二次根式 复习课件(43张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 412.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-19 14:06:47 | ||
图片预览






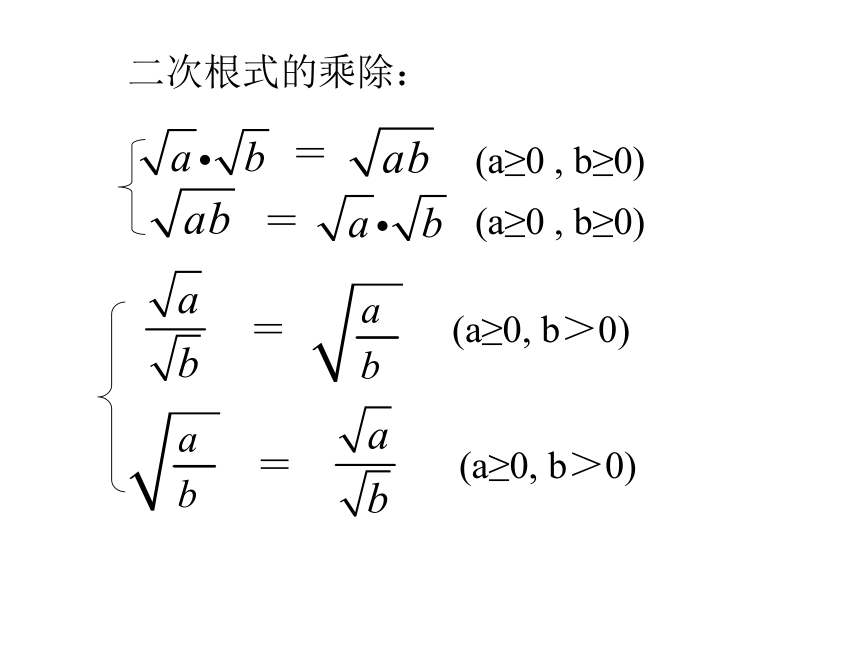




文档简介
课件43张PPT。
《二 次 根式》单元复习
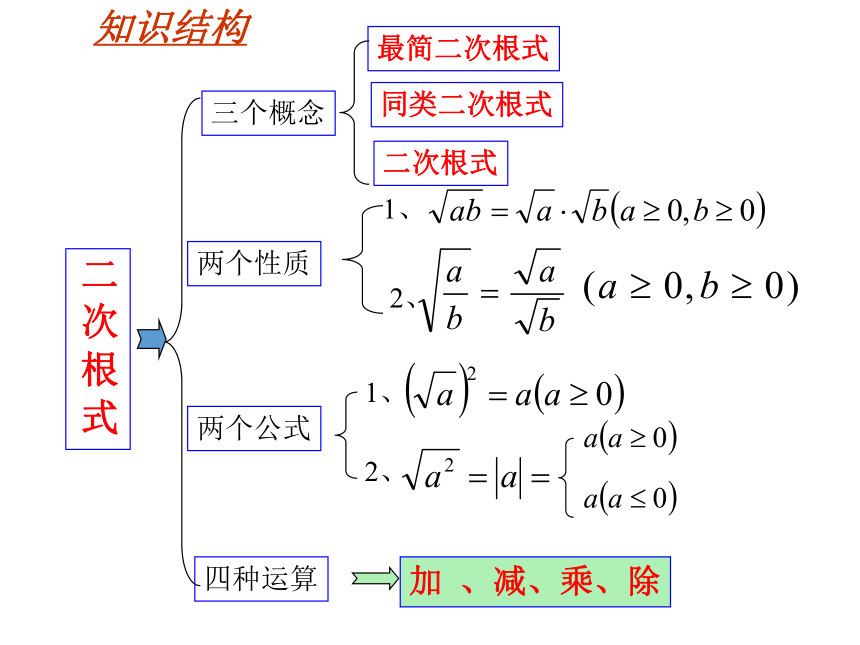
二 次 根 式知识结构被开方数a≥0;根指数为2.二次根式(2). a可以是数,也可以是式.(3). (4). a≥0, ≥0 (5).既可表示开方运算,也可表示运算的结果.(1).表示a的算术平方根( 双重非负性)二次根式有意义的条件 a≥0梳理二.二次根式的性质(1).(2).(3).(a≥0, ) 梳理三.二次根的乘除 (1)、积的算术平方根的性质
(2)、二次根式的乘法法则积的算术平方根,等于积中各因式的算术平方根的积.
(3)、商的算术平方根的性质
(4)、二次根式的除法法则商的算术平方根等于被除式的算术平方根除以除式的算术平方根二次根式的乘除:==(a≥0, b>0) 满足下列两个条件的二次根式,叫做最简二次式.
(1)被开方数的因数是整数,因式是整式.
(2)被开方数中不含开方开得尽的因数或因
式.
梳理四.最简二次根式的定义.
几个二次根式化为最简二次根式后,若被开方数相同,则这几个二次根式就叫做同类二次根式。梳理五 .同类二次根式的定义。 判断几个二次根式是否为同类二次根式的方法: 1、先化简:把各个二次根式都化为最简二次根式。 2、再观察:化简后的二次根式的被开方数是否相同。 二次根式加减时,先将二次根式化为最简二次根式,再把被开方数相同的二次根式进行合并。 注意:对被开方数相同的二次根式进行合并,实质是对被开方数相同的二次根式的系数进行合并。梳理六.二次根式加减法则梳理七. 混合运算法则1.先算乘方,再算乘除,最后算加减,
有括号先算先算括号里面的.2.对于二次根式的运算,各种运算
律照常使用,各种乘法公式照常
使用 (1)二次根式的运算结果,应该尽量化简,有理数的运算律在实数范围内仍可使用(2)二次根式的除法运算,通过采用化去分母中的根号的方法来进行,把分母中的根号化去叫做分母有理化.
注意的几点(3).判断几个二次根式是否是同类二次根式的关键是将几个二次根式化成最简二次根式后,被开方数相同.
(4).二次根式的乘除运算可以考虑先进行被开方数的
约分问题,再化简二次根式,而不一定要先将二次 根式化成最简二次根式,再约分.
(5).对有关二次根式的代数式的求值问题一般应对已知式先进行化简,代入化简后的待求式,同时还应注意
挖掘隐含条件和技巧的运用使求解更简捷.1.指出下列哪些是二次根式?√√√√ 2、 x取何值时,下列二次根式有意义?3.当x为怎样的实数时,下列各式有意义?x≥3x≤6∴3≤x≤6x≥1x≤1∴x=1x为任何实数.x为任何实数.4 函数 中,自
变量x的取值范围是 .5. 函数 中,自变量x的取值
范围是 .3
(2)当 时,
(3) ,
则X的取值范围是___
解:9DD 13:在实数范围内因式分解:4m2-7
例:二次根式的非负性的应用.解:由题意,得 x-4=0 且 2x+y=0解得 x=4,y=-8x-y=4-(-8)= 4+ 8 =12D16.(-5)×2×(-2)=2018.下列根式中,哪些是最简二次根式?√×××××√√√19.下列各组二次根式是否为同类二次根式?√×√×√如何判断? 21.若 ,则a的取值范围是( )A.
C. B.为任意数
20. 下列各式属于最简二次根式的是 ( )
A. B. C. D.D.BA22.一个台阶如图,阶梯每一层高15cm,宽25cm,长60cm.一只蚂蚁从A点爬到B点最短路程是多少?解:3 24. 实数p在数轴上的位置如图所示,化简 25:计算加减混合运算,应从左向右依次计算。解:原式=别漏了“1”.化简解:原式= 26.计算:
?
27.计算必做题:
复习题
知识技能 作业布置:
《二 次 根式》单元复习
二 次 根 式知识结构被开方数a≥0;根指数为2.二次根式(2). a可以是数,也可以是式.(3). (4). a≥0, ≥0 (5).既可表示开方运算,也可表示运算的结果.(1).表示a的算术平方根( 双重非负性)二次根式有意义的条件 a≥0梳理二.二次根式的性质(1).(2).(3).(a≥0, ) 梳理三.二次根的乘除 (1)、积的算术平方根的性质
(2)、二次根式的乘法法则积的算术平方根,等于积中各因式的算术平方根的积.
(3)、商的算术平方根的性质
(4)、二次根式的除法法则商的算术平方根等于被除式的算术平方根除以除式的算术平方根二次根式的乘除:==(a≥0, b>0) 满足下列两个条件的二次根式,叫做最简二次式.
(1)被开方数的因数是整数,因式是整式.
(2)被开方数中不含开方开得尽的因数或因
式.
梳理四.最简二次根式的定义.
几个二次根式化为最简二次根式后,若被开方数相同,则这几个二次根式就叫做同类二次根式。梳理五 .同类二次根式的定义。 判断几个二次根式是否为同类二次根式的方法: 1、先化简:把各个二次根式都化为最简二次根式。 2、再观察:化简后的二次根式的被开方数是否相同。 二次根式加减时,先将二次根式化为最简二次根式,再把被开方数相同的二次根式进行合并。 注意:对被开方数相同的二次根式进行合并,实质是对被开方数相同的二次根式的系数进行合并。梳理六.二次根式加减法则梳理七. 混合运算法则1.先算乘方,再算乘除,最后算加减,
有括号先算先算括号里面的.2.对于二次根式的运算,各种运算
律照常使用,各种乘法公式照常
使用 (1)二次根式的运算结果,应该尽量化简,有理数的运算律在实数范围内仍可使用(2)二次根式的除法运算,通过采用化去分母中的根号的方法来进行,把分母中的根号化去叫做分母有理化.
注意的几点(3).判断几个二次根式是否是同类二次根式的关键是将几个二次根式化成最简二次根式后,被开方数相同.
(4).二次根式的乘除运算可以考虑先进行被开方数的
约分问题,再化简二次根式,而不一定要先将二次 根式化成最简二次根式,再约分.
(5).对有关二次根式的代数式的求值问题一般应对已知式先进行化简,代入化简后的待求式,同时还应注意
挖掘隐含条件和技巧的运用使求解更简捷.1.指出下列哪些是二次根式?√√√√ 2、 x取何值时,下列二次根式有意义?3.当x为怎样的实数时,下列各式有意义?x≥3x≤6∴3≤x≤6x≥1x≤1∴x=1x为任何实数.x为任何实数.4 函数 中,自
变量x的取值范围是 .5. 函数 中,自变量x的取值
范围是 .3
(2)当 时,
(3) ,
则X的取值范围是___
解:9DD 13:在实数范围内因式分解:4m2-7
例:二次根式的非负性的应用.解:由题意,得 x-4=0 且 2x+y=0解得 x=4,y=-8x-y=4-(-8)= 4+ 8 =12D16.(-5)×2×(-2)=2018.下列根式中,哪些是最简二次根式?√×××××√√√19.下列各组二次根式是否为同类二次根式?√×√×√如何判断? 21.若 ,则a的取值范围是( )A.
C. B.为任意数
20. 下列各式属于最简二次根式的是 ( )
A. B. C. D.D.BA22.一个台阶如图,阶梯每一层高15cm,宽25cm,长60cm.一只蚂蚁从A点爬到B点最短路程是多少?解:3 24. 实数p在数轴上的位置如图所示,化简 25:计算加减混合运算,应从左向右依次计算。解:原式=别漏了“1”.化简解:原式= 26.计算:
?
27.计算必做题:
复习题
知识技能 作业布置:
