八年级数学下册第20章数据的整理与初步处理20.3数据的离散程度作业设计(含答案)新版华东师大版
文档属性
| 名称 | 八年级数学下册第20章数据的整理与初步处理20.3数据的离散程度作业设计(含答案)新版华东师大版 |

|
|
| 格式 | zip | ||
| 文件大小 | 142.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-19 16:34:47 | ||
图片预览



文档简介
20.3.1方差
一、选择题
1.数据7,9,10,11,13的方差是( )
A. B.2 C.3 D.4
2.如果一组数据x1,x2,…,xn的方差为4,则另一组数据x1+3,x2+3,…,xn+3的方差是( )
A.4 B.7 C.8 D.19
3.某村引进甲、乙两种水稻品种,各选6块条件相同的实验田,同时播种并核定亩产,结果甲、乙两种水稻的平均产量均为550 kg/亩,方差分别为S甲2=141.7,S乙2=433.3,则产量稳定,适合推广的品种为( )
A.甲、乙均可 B.甲 C.乙 D.无法确定
4.两名同学进行了10次三级蛙跳测试,经计算,他们的平均成绩相同,若要比较这两名同学的成绩哪一位更稳定,通常还需要比较他们的成绩的( )
A.众数 B.中位数 C.方差 D.以上都不对
5、在社会实践活动中,某同学对甲、乙、丙、丁四个城市一至五月份的白菜价格进行调查.四个城市5个月白菜的平均值均为3.50元,方差分别为S甲2=18.3,S乙2=17.4,S丙2=20.1,S丁2=12.5.一至五月份白菜价格最稳定的城市是( )
A、甲 B、乙 C、丙 D、丁
6、一次数学测试,某小组五名同学的成绩如下表所示(有两个数据被遮盖).
组员 甲 乙 丙 丁 戊 方差 平均成绩
得分 81 79 ■ 80 82 ■ 80
那么被遮盖的两个数据依次是( )
A.80,2 B.80, C.78,2 D.78,
7、下面是甲、乙两人10次射击成绩(环数)的条形统计图,则下列说法正确的是( )
A、甲比乙的成绩稳定 B、乙比甲的成绩稳定
C、甲、乙两人的成绩一样稳定 D、无法确定谁的成绩更稳定
8.某学习小组5位同学参加初中毕业生实验操作考试(满分20分)的平均成绩是16分.其中三位男生的方差为6(分2),两位女生的成绩分别为17分,15分.则这个学习小组5位同学考试分数的标准差为( )
A. B.2 C. D.6
9.已知样本x1,x2,…,xn的方差是2,则样本3x1+5,3x2+5,…,3xn+5的方差是( )
A.11 B.18 C.23 D.36
10.一次数学测试,某小组五名同学的成绩如下表所示(有两个数据被遮盖).
组员 甲 乙 丙 丁 戊 标准差 平均成绩
得分 81 79 ■ 80 82 ■ 80
那么被遮盖的两个数据依次是( )
A.80,2 B.80, C.78,2 D.78,
二、填空题
11、已知一组数据1,2,3,4,5的方差为2,则另一组数据11,12,13,14,15的方差为 _____.
12、一组数据按从小到大的顺序排列为1,2,3,x,4,5,若这组数据的中位数为3,则这组数据的方差是________.
13、已知一组数据﹣3,x,﹣2,3,1,6的中位数为1,则其方差为________.
14、八(2)班组织了一次经典朗读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):
那么乙队的平均成绩是________,方差是________.
15、跳远运动员小刚对训练效果进行测试,6次跳远的成绩(单位:m)如下:7.6,7.8,7.7,7.8,8.0,7.9.这6次成绩的平均数为7.8 m,方差为 m2.若小刚再跳两次,成绩分别为7.7 m,7.9 m,则小刚这8次跳远成绩的方差将________.(填“变大”“变小”或“不变”)
三、解答题
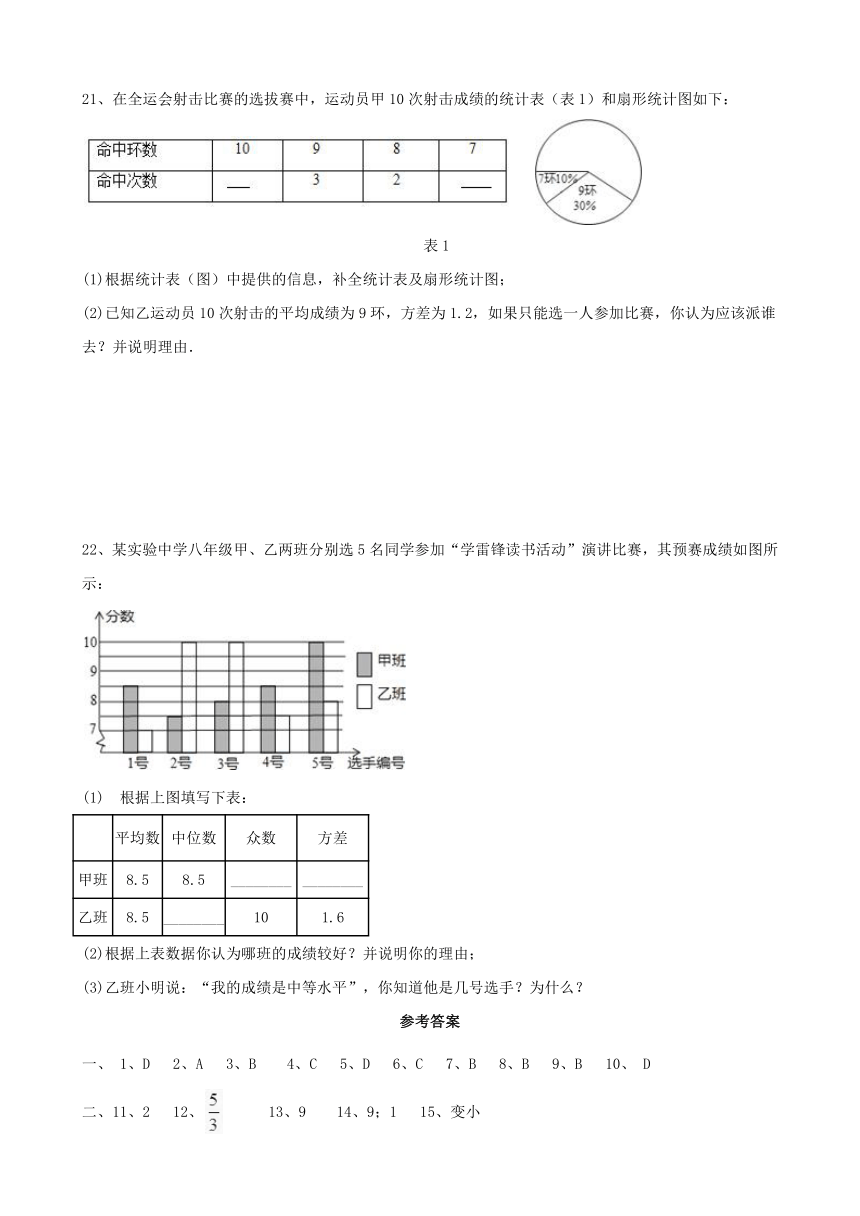
21、在全运会射击比赛的选拔赛中,运动员甲10次射击成绩的统计表(表1)和扇形统计图如下:
?
?????????????????????? 表1
(1)根据统计表(图)中提供的信息,补全统计表及扇形统计图;
(2)已知乙运动员10次射击的平均成绩为9环,方差为1.2,如果只能选一人参加比赛,你认为应该派谁去?并说明理由.
22、某实验中学八年级甲、乙两班分别选5名同学参加“学雷锋读书活动”演讲比赛,其预赛成绩如图所示:
(1)?根据上图填写下表:
平均数 中位数 众数 方差
甲班 8.5 8.5 ________ ________
乙班 8.5 ________ 10 1.6
(2)根据上表数据你认为哪班的成绩较好?并说明你的理由;
(3)乙班小明说:“我的成绩是中等水平”,你知道他是几号选手?为什么?
参考答案
一、 1、D 2、A 3、B 4、C 5、D 6、C 7、B 8、B 9、B 10、 D
二、11、2 12、? 13、9 14、9;1 15、变小
三、 21、(1)解:如下图所示:
(2)解答:应该派甲去.∵甲运动员10次射击的平均成绩为(10×4+9×3+8×2+7×1)÷10=9环,∴甲运动员10次射击的方差是 [(10-9)2×4+(9-9)2×3+(8-9)2×2+(7-9)2]=1,∵乙运动员10次射击的平均成绩为9环,方差为1.2,大于甲的方差,∴如果只能选一人参加比赛,认为应该派甲去.
22、(1)8;8.5;0.7
(2)从平均数看,因两班平均数相同,则甲、乙班的成绩一样好;从中位数看,甲的中位数高,所以甲班的成绩较好;从众数看,乙班的分数高,所以乙班成绩较好;从方差看,甲班的方差小,所以甲班的成绩更稳定.
(3)小明是5号选手.因为乙班的成绩的中位数是8,所以小明的成绩是8分,则小明是5号选手.
20.3.2用计算器求方差
一、选择题
1.在进行统计计算时,为了清除前一步输错的数据,应按键( )
A.STAT B.DEL C. DCA D.DATA
2.下列说法正确的是( )
A.一个游戏的中奖概率是,则做10次这样的游戏一定会中奖
B.为了解全国中学生的心理健康情况,应该采用普查的方式
C.一组数据6,8,7,8,8,9,10的众数和中位数都是8
D.若甲组数据的方差,乙组数据的方差,则乙组数据比甲组数据稳定
3.某同学使用计算器求30个数据的平均数时,错将其中一个数据105输入为15,那么所求出平均数与实际平均数的差是( )
A.3.5 B.3 C.0.5 D.-3
4.甲、乙两名同学在相同的条件下各射击5次,命中的环数如下表:
那么下列结论正确的是( )
A.甲的平均数是7,方差是1.2 B.乙的平均数是7,方差是1.2
C.甲的平均数是8,方差是1.2 D.乙的平均数是8,方差是0.8
5.已知一组数据70,29,71,72,81,73,105,69,用计算器求得这组数据的方差为(精确到0.01)( )
A.378 B.377.69 C.378.70 D.378.69
6.已知一个样本a,4,2,5,3,它的平均数是3,则这个样本的标准差为( )
A.0 B.1 C. D.2
7.甲乙两人5次射击命中的次数如下:
则这两人次射击命中的环数的平均数都为8,则甲的方差与乙的方差的大小关系为( )
A.甲的方差大 B.乙的方差大 C.两个方差相等 D.无法判断
8.甲、乙两台包装机同时包装质量为500克的物品,从中各抽出10袋,测得其实际质量分别如下(单位:克)
借助计算器判断,包装机包装的10袋物品的质量比较稳定的是( )
A.甲 B.乙 C.一样稳定 D.无法判断
9.我校准备挑选一名跳高运动员参加全市中学生运动会,对跳高运动队的甲、乙两名运动员进行了8次选拔比赛.他们的成绩(单位:m)如下:
借助计算器判断运动员的成绩更为稳定的是( )
A.甲 B.乙 C.一样稳定 D.无法判断
10.甲、乙、丙三名射击运动员在某场测试中各射击20次,3人的测试成绩如下表:
借助计算器判断甲、乙、丙3名运动员测试成绩最稳定的是( )
A.甲 B.乙 C.丙 D.三名运动员一样稳定
二、填空题
11.极差、 、 都是用来描述一组数据的 情况的特征数据.
12.利用计算器求标准差和方差时,首先要进入 计算状态,再依次输入每一个数据,最后按求方差的功能键 ,即可得出结果.
13.打开计算器后,按键 、 进入统计状态.
14.输入数据后,按 键计算这组数据的方差.
15.输入数据后,按 键计算这组数据的标准差.
三、解答题
16.已知一组数据6,3,4,7,6,3,5,6.
(1)求这组数据的平均数、众数、中位数;
(2)求这组数据的方差和标准差.
17.为了从小明和小丽两人中选拔一个参加学校军训射击比赛,现对他们的射击成绩进行了测试,10次打靶命中的环数如下:
小明:10,7,8,8,8,8,8,8,9,6;
小丽:8,8,8,8,5,8,8,9,9,9
借助计算器计算小明和小丽命中环数的方差和标准差,哪一个人的射击成绩比较稳定?.
18.用计算器计算下列一组数据的平均数、标准差与方差:85,75,92,98,63,90,88,56,77,95.(保留到小数点的后两位)
参考答案
1. B 解析:在进行统计计算时,为了清除前一步输错的数据,应按键“DEL”.故选B.
2. C 解析:一个游戏的中奖概率是,则做10次这样的游戏不一定会中奖,所以A选择的说法错误;为了解全国中学生的心理健康情况,应该采用抽样调查的方式,所以B选项的说法错误;C选项的说法正确;若甲组数据的方差,乙组数据的方差,则甲组数据比乙组数据稳定,所以D选项的说法错误.故选C.
3. D 解析:求30个数据的平均数时,错将其中一个数据105输入为15,即使总和减少了90,所以求出的平均数与实际平均数的差是.故选D.
4. A 解析:甲的平均数:=7,方差:=1.2;乙的平均数:,方差:=0.8.故选A.
5. D 解析:将计算器功能模式设定为统计模式后一次按键70 DATA 29 DATA 71 DATA …69 DATA输入所有数据;再按SHIFT X-M =即可求得这组数据的方差,所以选D.
6. C 解析:由题意,可得a+4+2+5+3=15,即a=1,所以这个样本的方差为,所以这个样本的标准差为.故选C.
7. A 解析:甲的方差为,乙的方差为,所以甲的方差大.故选A.
8. B 解析:借助计算器可以求得甲包装机的方差为0.806,乙包装机的方差为0.172,所以乙的方差比较小即乙包装机包装的10袋物品的质量比较稳定.故选B.
9. A 解析:借助计算器可以求得甲运动员的方差为0.0006,乙运动员的方差为0.0315,所以甲的方差比较小即甲运动员的成绩更稳定.故选A.
10. A 解析:甲运动员成绩的方差为0.65,乙运动员成绩的方差为1.45,丙运动员成绩的方差为1.25,所以甲运动员成绩的方差较小,所以甲运动员的测试成绩最稳定.故选A.
二、11.方差|标准差|波动 解析:极差、方差、标准差都是反映一组数据的波动情况的.
12. MODE| 解析:利用计算器求标准差和方差时,首先要进入MODE计算状态,再依次输入每一个数据,最后按求方差的功能键,即可得出结果.
13. MODE|2 解析:根据科学计算器的使用,打开计算器后,要启动计算器的统计计算功能应按键MODE 2.
14. SHIFT X-M =解析:输入数据后,按SHIFT X-M =键计算这组数据的方差.
15. SHIFT RM =解析:输入数据后,按SHIFT RM =键计算这组数据的标准差.
三、16. 解:(1)按从小到大的顺序排列数据为:3,3,4,5,6,6,6,7,其中众数是6,中位数是,平均数为.
(2)方差为,标准差为.
17. 解:①按开机键ON/C后,首先将计算器功能模式设定为为统计模式;②依次按键:10 DATA 7 DATA 8 DATA …6 DATA输入所有数据;再按SHIFT X-M =求得小明射击的方差=1,按SHIFT RM =求得标准差S=1;同理可求得小丽射击的方差=1.2,标准差S=1.095445115,所以第二组数据的方差约为1.2,第一组数据的方差为1,因为1.2>1,所以第二组数据的离散程度较大,小明射击成绩比小丽稳定.
18.解:这一组数据的平均数为=81.9,方差为S2=[(85-81.9)2+(75-81.9)2+(92-81.9)2+(98-81.9)2+(63-81.9)2+(90-81.9)2+(88-81.9)2+(56-81.9)2+(77-81.9)2+(95-81.9)2]=174.49,标准差为S≈13.21.
一、选择题
1.数据7,9,10,11,13的方差是( )
A. B.2 C.3 D.4
2.如果一组数据x1,x2,…,xn的方差为4,则另一组数据x1+3,x2+3,…,xn+3的方差是( )
A.4 B.7 C.8 D.19
3.某村引进甲、乙两种水稻品种,各选6块条件相同的实验田,同时播种并核定亩产,结果甲、乙两种水稻的平均产量均为550 kg/亩,方差分别为S甲2=141.7,S乙2=433.3,则产量稳定,适合推广的品种为( )
A.甲、乙均可 B.甲 C.乙 D.无法确定
4.两名同学进行了10次三级蛙跳测试,经计算,他们的平均成绩相同,若要比较这两名同学的成绩哪一位更稳定,通常还需要比较他们的成绩的( )
A.众数 B.中位数 C.方差 D.以上都不对
5、在社会实践活动中,某同学对甲、乙、丙、丁四个城市一至五月份的白菜价格进行调查.四个城市5个月白菜的平均值均为3.50元,方差分别为S甲2=18.3,S乙2=17.4,S丙2=20.1,S丁2=12.5.一至五月份白菜价格最稳定的城市是( )
A、甲 B、乙 C、丙 D、丁
6、一次数学测试,某小组五名同学的成绩如下表所示(有两个数据被遮盖).
组员 甲 乙 丙 丁 戊 方差 平均成绩
得分 81 79 ■ 80 82 ■ 80
那么被遮盖的两个数据依次是( )
A.80,2 B.80, C.78,2 D.78,
7、下面是甲、乙两人10次射击成绩(环数)的条形统计图,则下列说法正确的是( )
A、甲比乙的成绩稳定 B、乙比甲的成绩稳定
C、甲、乙两人的成绩一样稳定 D、无法确定谁的成绩更稳定
8.某学习小组5位同学参加初中毕业生实验操作考试(满分20分)的平均成绩是16分.其中三位男生的方差为6(分2),两位女生的成绩分别为17分,15分.则这个学习小组5位同学考试分数的标准差为( )
A. B.2 C. D.6
9.已知样本x1,x2,…,xn的方差是2,则样本3x1+5,3x2+5,…,3xn+5的方差是( )
A.11 B.18 C.23 D.36
10.一次数学测试,某小组五名同学的成绩如下表所示(有两个数据被遮盖).
组员 甲 乙 丙 丁 戊 标准差 平均成绩
得分 81 79 ■ 80 82 ■ 80
那么被遮盖的两个数据依次是( )
A.80,2 B.80, C.78,2 D.78,
二、填空题
11、已知一组数据1,2,3,4,5的方差为2,则另一组数据11,12,13,14,15的方差为 _____.
12、一组数据按从小到大的顺序排列为1,2,3,x,4,5,若这组数据的中位数为3,则这组数据的方差是________.
13、已知一组数据﹣3,x,﹣2,3,1,6的中位数为1,则其方差为________.
14、八(2)班组织了一次经典朗读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):
那么乙队的平均成绩是________,方差是________.
15、跳远运动员小刚对训练效果进行测试,6次跳远的成绩(单位:m)如下:7.6,7.8,7.7,7.8,8.0,7.9.这6次成绩的平均数为7.8 m,方差为 m2.若小刚再跳两次,成绩分别为7.7 m,7.9 m,则小刚这8次跳远成绩的方差将________.(填“变大”“变小”或“不变”)
三、解答题
21、在全运会射击比赛的选拔赛中,运动员甲10次射击成绩的统计表(表1)和扇形统计图如下:
?
?????????????????????? 表1
(1)根据统计表(图)中提供的信息,补全统计表及扇形统计图;
(2)已知乙运动员10次射击的平均成绩为9环,方差为1.2,如果只能选一人参加比赛,你认为应该派谁去?并说明理由.
22、某实验中学八年级甲、乙两班分别选5名同学参加“学雷锋读书活动”演讲比赛,其预赛成绩如图所示:
(1)?根据上图填写下表:
平均数 中位数 众数 方差
甲班 8.5 8.5 ________ ________
乙班 8.5 ________ 10 1.6
(2)根据上表数据你认为哪班的成绩较好?并说明你的理由;
(3)乙班小明说:“我的成绩是中等水平”,你知道他是几号选手?为什么?
参考答案
一、 1、D 2、A 3、B 4、C 5、D 6、C 7、B 8、B 9、B 10、 D
二、11、2 12、? 13、9 14、9;1 15、变小
三、 21、(1)解:如下图所示:
(2)解答:应该派甲去.∵甲运动员10次射击的平均成绩为(10×4+9×3+8×2+7×1)÷10=9环,∴甲运动员10次射击的方差是 [(10-9)2×4+(9-9)2×3+(8-9)2×2+(7-9)2]=1,∵乙运动员10次射击的平均成绩为9环,方差为1.2,大于甲的方差,∴如果只能选一人参加比赛,认为应该派甲去.
22、(1)8;8.5;0.7
(2)从平均数看,因两班平均数相同,则甲、乙班的成绩一样好;从中位数看,甲的中位数高,所以甲班的成绩较好;从众数看,乙班的分数高,所以乙班成绩较好;从方差看,甲班的方差小,所以甲班的成绩更稳定.
(3)小明是5号选手.因为乙班的成绩的中位数是8,所以小明的成绩是8分,则小明是5号选手.
20.3.2用计算器求方差
一、选择题
1.在进行统计计算时,为了清除前一步输错的数据,应按键( )
A.STAT B.DEL C. DCA D.DATA
2.下列说法正确的是( )
A.一个游戏的中奖概率是,则做10次这样的游戏一定会中奖
B.为了解全国中学生的心理健康情况,应该采用普查的方式
C.一组数据6,8,7,8,8,9,10的众数和中位数都是8
D.若甲组数据的方差,乙组数据的方差,则乙组数据比甲组数据稳定
3.某同学使用计算器求30个数据的平均数时,错将其中一个数据105输入为15,那么所求出平均数与实际平均数的差是( )
A.3.5 B.3 C.0.5 D.-3
4.甲、乙两名同学在相同的条件下各射击5次,命中的环数如下表:
那么下列结论正确的是( )
A.甲的平均数是7,方差是1.2 B.乙的平均数是7,方差是1.2
C.甲的平均数是8,方差是1.2 D.乙的平均数是8,方差是0.8
5.已知一组数据70,29,71,72,81,73,105,69,用计算器求得这组数据的方差为(精确到0.01)( )
A.378 B.377.69 C.378.70 D.378.69
6.已知一个样本a,4,2,5,3,它的平均数是3,则这个样本的标准差为( )
A.0 B.1 C. D.2
7.甲乙两人5次射击命中的次数如下:
则这两人次射击命中的环数的平均数都为8,则甲的方差与乙的方差的大小关系为( )
A.甲的方差大 B.乙的方差大 C.两个方差相等 D.无法判断
8.甲、乙两台包装机同时包装质量为500克的物品,从中各抽出10袋,测得其实际质量分别如下(单位:克)
借助计算器判断,包装机包装的10袋物品的质量比较稳定的是( )
A.甲 B.乙 C.一样稳定 D.无法判断
9.我校准备挑选一名跳高运动员参加全市中学生运动会,对跳高运动队的甲、乙两名运动员进行了8次选拔比赛.他们的成绩(单位:m)如下:
借助计算器判断运动员的成绩更为稳定的是( )
A.甲 B.乙 C.一样稳定 D.无法判断
10.甲、乙、丙三名射击运动员在某场测试中各射击20次,3人的测试成绩如下表:
借助计算器判断甲、乙、丙3名运动员测试成绩最稳定的是( )
A.甲 B.乙 C.丙 D.三名运动员一样稳定
二、填空题
11.极差、 、 都是用来描述一组数据的 情况的特征数据.
12.利用计算器求标准差和方差时,首先要进入 计算状态,再依次输入每一个数据,最后按求方差的功能键 ,即可得出结果.
13.打开计算器后,按键 、 进入统计状态.
14.输入数据后,按 键计算这组数据的方差.
15.输入数据后,按 键计算这组数据的标准差.
三、解答题
16.已知一组数据6,3,4,7,6,3,5,6.
(1)求这组数据的平均数、众数、中位数;
(2)求这组数据的方差和标准差.
17.为了从小明和小丽两人中选拔一个参加学校军训射击比赛,现对他们的射击成绩进行了测试,10次打靶命中的环数如下:
小明:10,7,8,8,8,8,8,8,9,6;
小丽:8,8,8,8,5,8,8,9,9,9
借助计算器计算小明和小丽命中环数的方差和标准差,哪一个人的射击成绩比较稳定?.
18.用计算器计算下列一组数据的平均数、标准差与方差:85,75,92,98,63,90,88,56,77,95.(保留到小数点的后两位)
参考答案
1. B 解析:在进行统计计算时,为了清除前一步输错的数据,应按键“DEL”.故选B.
2. C 解析:一个游戏的中奖概率是,则做10次这样的游戏不一定会中奖,所以A选择的说法错误;为了解全国中学生的心理健康情况,应该采用抽样调查的方式,所以B选项的说法错误;C选项的说法正确;若甲组数据的方差,乙组数据的方差,则甲组数据比乙组数据稳定,所以D选项的说法错误.故选C.
3. D 解析:求30个数据的平均数时,错将其中一个数据105输入为15,即使总和减少了90,所以求出的平均数与实际平均数的差是.故选D.
4. A 解析:甲的平均数:=7,方差:=1.2;乙的平均数:,方差:=0.8.故选A.
5. D 解析:将计算器功能模式设定为统计模式后一次按键70 DATA 29 DATA 71 DATA …69 DATA输入所有数据;再按SHIFT X-M =即可求得这组数据的方差,所以选D.
6. C 解析:由题意,可得a+4+2+5+3=15,即a=1,所以这个样本的方差为,所以这个样本的标准差为.故选C.
7. A 解析:甲的方差为,乙的方差为,所以甲的方差大.故选A.
8. B 解析:借助计算器可以求得甲包装机的方差为0.806,乙包装机的方差为0.172,所以乙的方差比较小即乙包装机包装的10袋物品的质量比较稳定.故选B.
9. A 解析:借助计算器可以求得甲运动员的方差为0.0006,乙运动员的方差为0.0315,所以甲的方差比较小即甲运动员的成绩更稳定.故选A.
10. A 解析:甲运动员成绩的方差为0.65,乙运动员成绩的方差为1.45,丙运动员成绩的方差为1.25,所以甲运动员成绩的方差较小,所以甲运动员的测试成绩最稳定.故选A.
二、11.方差|标准差|波动 解析:极差、方差、标准差都是反映一组数据的波动情况的.
12. MODE| 解析:利用计算器求标准差和方差时,首先要进入MODE计算状态,再依次输入每一个数据,最后按求方差的功能键,即可得出结果.
13. MODE|2 解析:根据科学计算器的使用,打开计算器后,要启动计算器的统计计算功能应按键MODE 2.
14. SHIFT X-M =解析:输入数据后,按SHIFT X-M =键计算这组数据的方差.
15. SHIFT RM =解析:输入数据后,按SHIFT RM =键计算这组数据的标准差.
三、16. 解:(1)按从小到大的顺序排列数据为:3,3,4,5,6,6,6,7,其中众数是6,中位数是,平均数为.
(2)方差为,标准差为.
17. 解:①按开机键ON/C后,首先将计算器功能模式设定为为统计模式;②依次按键:10 DATA 7 DATA 8 DATA …6 DATA输入所有数据;再按SHIFT X-M =求得小明射击的方差=1,按SHIFT RM =求得标准差S=1;同理可求得小丽射击的方差=1.2,标准差S=1.095445115,所以第二组数据的方差约为1.2,第一组数据的方差为1,因为1.2>1,所以第二组数据的离散程度较大,小明射击成绩比小丽稳定.
18.解:这一组数据的平均数为=81.9,方差为S2=[(85-81.9)2+(75-81.9)2+(92-81.9)2+(98-81.9)2+(63-81.9)2+(90-81.9)2+(88-81.9)2+(56-81.9)2+(77-81.9)2+(95-81.9)2]=174.49,标准差为S≈13.21.
