高中数学人教A版必修5《等差数列的前n项和》第1课时课件(共20张PPT)
文档属性
| 名称 | 高中数学人教A版必修5《等差数列的前n项和》第1课时课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-20 10:38:12 | ||
图片预览








文档简介
(共21张PPT)
等差数列的前n项和
(第1课时)
马鞍山中加双语学校数学组
李 强
课题导入
世界三大数学家
得到数列 1,2,3,4, … ,100
问题1
目标引领
1.掌握等差数列前n项和公式,
能较熟练应用等差数列前n项和公式求和。
2.了解等差数列前n项和推导过程,了解倒序求和法的使用
独立自学
1.什么是等差数列
2.等差数列的通项公式是什么
3.等差数列的性质有哪些
泰姬陵坐落于印度古都阿格,是十七世纪莫卧儿帝国皇帝沙杰罕为纪念其爱妃所建,她宏伟壮观,纯白大理石砌建而成的主体建筑叫人心醉神迷,成为世界七大奇迹之一.陵寝以宝石镶饰,图案之细致令人叫绝.
传说陵寝中有一个三角形图案,以相同大小的圆宝石镶饰而成,共有100层(见左图),奢靡之程度,可见一斑.
你知道这个图案一共花了多少宝石吗?
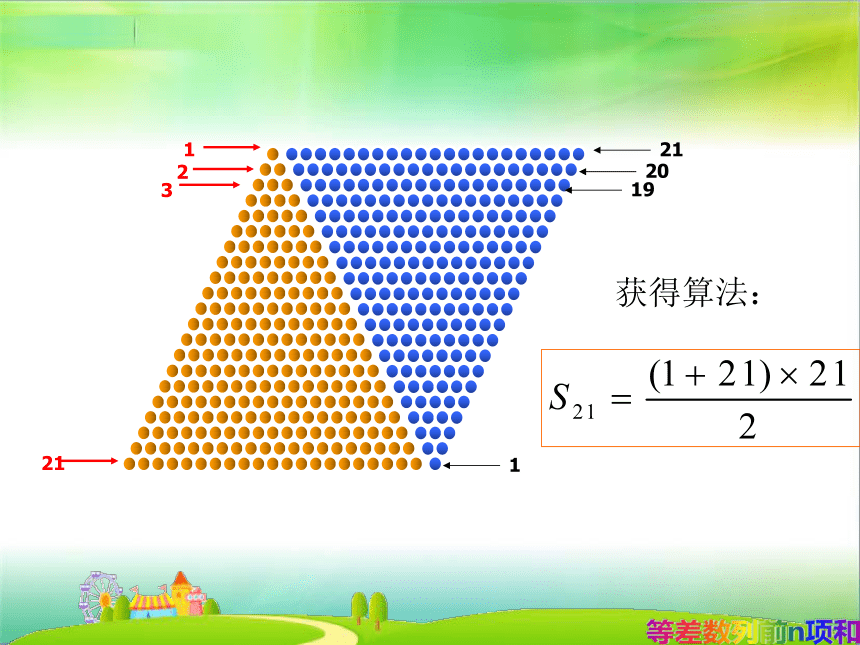
问题2:图案中,第1层到第21层一共有多少颗宝石?
引导探究
所以S21=
(1+21)×21
?
?
首项
尾项
?
总
和
?
项数
=231
问题 1:
1+2+3+······+100=?
(一)问题情景
下面再来看1+2+3+…+98+99+100的高斯算法.
设S100=1 + 2 + 3 +…+98+99+100
反序S100=100+99+98+…+ 3+ 2 + 1
多少个101 ?
100个101
所以S100=
(1+100)×100
?
?
首项
尾项
?
总
和
?
项数
=5 050
等差数列的前n项和公式的推导
由等差数列
的前n项和
得
例1. 根据下列条件,求相应的等差数列的前n项和
等差数列的前n项和公式的其它形式
例2:等差数列-10,-6,-2,2,·······
(1)求其前4项和;
(2)求其前100项和
(3)前多少项和是54 ?
解:
当堂诊学
练习
(1) a1=75,a7=105,求S7及d.
(2) a1=-10,d=4,Sn=54,求n及a21.
(3) S5=25, S10= 100,求a1及d.
1.经历了等差数列前n项和公式推倒的过程,
将高斯算法进行推广。
强化补清
课本118页,习题3.3第2 、 3、4
思考:1.等差数列前n项和公式和二次函数有什么关系
浅薄的学识使人远离神,广博的学识使人接近神。——高斯
数学,科学的皇后;算术,数学的皇后。——高斯
等差数列的前n项和
(第1课时)
马鞍山中加双语学校数学组
李 强
课题导入
世界三大数学家
得到数列 1,2,3,4, … ,100
问题1
目标引领
1.掌握等差数列前n项和公式,
能较熟练应用等差数列前n项和公式求和。
2.了解等差数列前n项和推导过程,了解倒序求和法的使用
独立自学
1.什么是等差数列
2.等差数列的通项公式是什么
3.等差数列的性质有哪些
泰姬陵坐落于印度古都阿格,是十七世纪莫卧儿帝国皇帝沙杰罕为纪念其爱妃所建,她宏伟壮观,纯白大理石砌建而成的主体建筑叫人心醉神迷,成为世界七大奇迹之一.陵寝以宝石镶饰,图案之细致令人叫绝.
传说陵寝中有一个三角形图案,以相同大小的圆宝石镶饰而成,共有100层(见左图),奢靡之程度,可见一斑.
你知道这个图案一共花了多少宝石吗?
问题2:图案中,第1层到第21层一共有多少颗宝石?
引导探究
所以S21=
(1+21)×21
?
?
首项
尾项
?
总
和
?
项数
=231
问题 1:
1+2+3+······+100=?
(一)问题情景
下面再来看1+2+3+…+98+99+100的高斯算法.
设S100=1 + 2 + 3 +…+98+99+100
反序S100=100+99+98+…+ 3+ 2 + 1
多少个101 ?
100个101
所以S100=
(1+100)×100
?
?
首项
尾项
?
总
和
?
项数
=5 050
等差数列的前n项和公式的推导
由等差数列
的前n项和
得
例1. 根据下列条件,求相应的等差数列的前n项和
等差数列的前n项和公式的其它形式
例2:等差数列-10,-6,-2,2,·······
(1)求其前4项和;
(2)求其前100项和
(3)前多少项和是54 ?
解:
当堂诊学
练习
(1) a1=75,a7=105,求S7及d.
(2) a1=-10,d=4,Sn=54,求n及a21.
(3) S5=25, S10= 100,求a1及d.
1.经历了等差数列前n项和公式推倒的过程,
将高斯算法进行推广。
强化补清
课本118页,习题3.3第2 、 3、4
思考:1.等差数列前n项和公式和二次函数有什么关系
浅薄的学识使人远离神,广博的学识使人接近神。——高斯
数学,科学的皇后;算术,数学的皇后。——高斯
