18.1.2 平行四边形的判定同步测试题(含解析)
文档属性
| 名称 | 18.1.2 平行四边形的判定同步测试题(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-19 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
人教版2019-2020学年八年级下学期
18.1.2平行四边形的判定
(时间60分钟 总分100分)
一、选择题(每小题5分,共30分)
1.在四边形ABCD中,AD||BC,若ABCD是平行四边形,则还应满足( )
A. B. C. D.
2.如图,在-ABC中,点D,E分别是边AB,BC的中点,若DBE的周长是6,则ABC的周长是( )
A.8 B.10 C.12 D.14.
3.下面给出了四边形ABCD中的度数之比,其中能判定四边形ABCD是平行四边形的是( )
A.1:2:3:4 B.2:2:3:3 C.2:3:2:3 D.2:3:3:2.
4.如图,在ABCD中,BF平分ABC,交ADF点F,CE平分BCD交AD于点E,AB=6,BF=2,则BC长为( )
A.8 B.10 C. 12 D. 14
5.已知ABCD的两条对角线AC=18,BD=8,则BC的长度可能为( )
A.5 B.10 C.13 D.26
6.如图,在ABC中,AB=4,AC=3,AD、AE分别是其角平分线和中线,过点C作CGAD于F,交AB于G,连接EF,则线段EF的长为( )
A. B.1 C. D.7
二、填空题(每小题5分,共20分)
7.将两根木条AC,BD的中点重叠,并用钉子固定,则四边形ABCD为平行四边形,理由是__________________________________________________________________
8.如图,在四边形ABCD中,对角线AC,BD交于点O,AD//BC,请添加一个条件:_______使四边形ABCD是平行四边形。
9.如图,以ABC的顶点A为圆心,以BC长为半径作弧,再以顶点C为圆心,以AB长为半径作弧,两引交于点D,连接AD,CD.若B=65,则ADC的大小为________
10.如图,ABCD中,,E,F分别在CD和BC的延长线上,A,AB的长为________
三、解答题(共5题,共50分)
11.如图,在ABC中,D、E分别是AB,AC的中点,过点E作EF||AB,交BC于点F,求证:四边形DBFE是平行四边形:
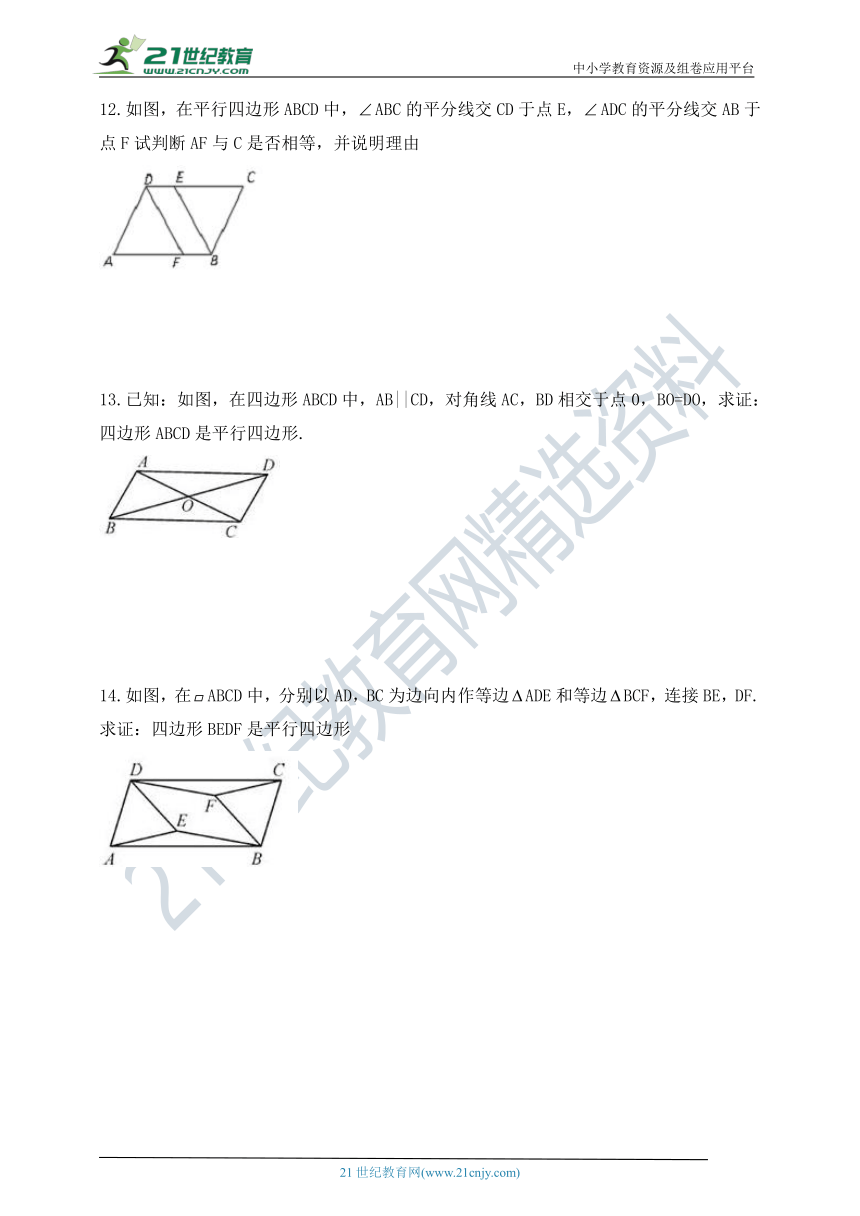
12.如图,在平行四边形ABCD中,ABC的平分线交CD于点E,ADC的平分线交AB于点F试判断AF与C是否相等,并说明理由
13.已知:如图,在四边形ABCD中,AB||CD,对角线AC,BD相交于点0,BO=DO,求证:四边形ABCD是平行四边形.
14.如图,在ABCD中,分别以AD,BC为边向内作等边ADE和等边BCF,连接BE,DF.求证:四边形BEDF是平行四边形
15.已知,如图,在ABCD中,AEBC,垂足为E,CE=CD,点F为CE的中点,点G为CD上的一点,连接DF,EG,AG,
(1)若CF=2,AE=3,求BE的长
(2)求证:
答案
1.【解析】结合平行四边形判定法则,可知还需要满足AB||CD,可知应该满足,故选D。
2.【解析】三角形ABC中,DE为中位线,可知周长是周长的一半,故选C。
3.【解析】两组对角分别相等的四边形是平行四边形,根据两组对角分别相等的四边形是平行四边形,.所以选C
4.【解析】因为四边形ABCD是平行四边形,
,因为BF平分 ABC,,则
,同理可证:DE=DC=6,,即6+6-AD=2,解得:AD=10;,故答案为:10
5.【解析】ABCD的两条对角线AC=18,BD=8,,所以56.【解析】因为AD 是BAC的平分线,,
,在AFG和AFC中,,
,所以F是CG的中点,又因为点E是BC的中点,所以EF是CBG的中位线,,故答案为,故选A。
7.【解析】对角线互相平分的四边形是平行四边形
8.【解析】AD=BC
9.【解析】结合平行四边形判定,对边相等的四边形为平行四边形,可知
10.【解析】因为四边形ABCD是平行四边形,,
所以四边形ABDE是平行四边形,所以,即D为CE中点,
,,,,,
11.【解析】证明:因为D、E分别是AB,AC的中点,所以DE是ABC的中位线
,又,所以四边形DBFE是平行四边形;
12.【解析】因为四边形ABCD是平行四边形,
又,,,
13.【解析】,,又
,,所以四边形ABCD是平行四边形.
14.【解析】因为四边形ABCD是平行四边形,
又因为ADE和CBF都是等边三角形,
,,
所以四边形BEDF是平行四边形.
15.【解析】(1)因为CE=CD,点F为CE的中点,CF=2,所以DC=CE=2CF=4,因为四边形ABCD是平行四边形,所以AB=CD=4,,,在RtABE中,由勾股定理得
(2)证明:过G作GMAE于M,,
因为在DCF和ECG中,,,
,,即G为CD中点,,所以.M为AE中点,,,,
,,
_21?????????è?????(www.21cnjy.com)_
人教版2019-2020学年八年级下学期
18.1.2平行四边形的判定
(时间60分钟 总分100分)
一、选择题(每小题5分,共30分)
1.在四边形ABCD中,AD||BC,若ABCD是平行四边形,则还应满足( )
A. B. C. D.
2.如图,在-ABC中,点D,E分别是边AB,BC的中点,若DBE的周长是6,则ABC的周长是( )
A.8 B.10 C.12 D.14.
3.下面给出了四边形ABCD中的度数之比,其中能判定四边形ABCD是平行四边形的是( )
A.1:2:3:4 B.2:2:3:3 C.2:3:2:3 D.2:3:3:2.
4.如图,在ABCD中,BF平分ABC,交ADF点F,CE平分BCD交AD于点E,AB=6,BF=2,则BC长为( )
A.8 B.10 C. 12 D. 14
5.已知ABCD的两条对角线AC=18,BD=8,则BC的长度可能为( )
A.5 B.10 C.13 D.26
6.如图,在ABC中,AB=4,AC=3,AD、AE分别是其角平分线和中线,过点C作CGAD于F,交AB于G,连接EF,则线段EF的长为( )
A. B.1 C. D.7
二、填空题(每小题5分,共20分)
7.将两根木条AC,BD的中点重叠,并用钉子固定,则四边形ABCD为平行四边形,理由是__________________________________________________________________
8.如图,在四边形ABCD中,对角线AC,BD交于点O,AD//BC,请添加一个条件:_______使四边形ABCD是平行四边形。
9.如图,以ABC的顶点A为圆心,以BC长为半径作弧,再以顶点C为圆心,以AB长为半径作弧,两引交于点D,连接AD,CD.若B=65,则ADC的大小为________
10.如图,ABCD中,,E,F分别在CD和BC的延长线上,A,AB的长为________
三、解答题(共5题,共50分)
11.如图,在ABC中,D、E分别是AB,AC的中点,过点E作EF||AB,交BC于点F,求证:四边形DBFE是平行四边形:
12.如图,在平行四边形ABCD中,ABC的平分线交CD于点E,ADC的平分线交AB于点F试判断AF与C是否相等,并说明理由
13.已知:如图,在四边形ABCD中,AB||CD,对角线AC,BD相交于点0,BO=DO,求证:四边形ABCD是平行四边形.
14.如图,在ABCD中,分别以AD,BC为边向内作等边ADE和等边BCF,连接BE,DF.求证:四边形BEDF是平行四边形
15.已知,如图,在ABCD中,AEBC,垂足为E,CE=CD,点F为CE的中点,点G为CD上的一点,连接DF,EG,AG,
(1)若CF=2,AE=3,求BE的长
(2)求证:
答案
1.【解析】结合平行四边形判定法则,可知还需要满足AB||CD,可知应该满足,故选D。
2.【解析】三角形ABC中,DE为中位线,可知周长是周长的一半,故选C。
3.【解析】两组对角分别相等的四边形是平行四边形,根据两组对角分别相等的四边形是平行四边形,.所以选C
4.【解析】因为四边形ABCD是平行四边形,
,因为BF平分 ABC,,则
,同理可证:DE=DC=6,,即6+6-AD=2,解得:AD=10;,故答案为:10
5.【解析】ABCD的两条对角线AC=18,BD=8,,所以5
,在AFG和AFC中,,
,所以F是CG的中点,又因为点E是BC的中点,所以EF是CBG的中位线,,故答案为,故选A。
7.【解析】对角线互相平分的四边形是平行四边形
8.【解析】AD=BC
9.【解析】结合平行四边形判定,对边相等的四边形为平行四边形,可知
10.【解析】因为四边形ABCD是平行四边形,,
所以四边形ABDE是平行四边形,所以,即D为CE中点,
,,,,,
11.【解析】证明:因为D、E分别是AB,AC的中点,所以DE是ABC的中位线
,又,所以四边形DBFE是平行四边形;
12.【解析】因为四边形ABCD是平行四边形,
又,,,
13.【解析】,,又
,,所以四边形ABCD是平行四边形.
14.【解析】因为四边形ABCD是平行四边形,
又因为ADE和CBF都是等边三角形,
,,
所以四边形BEDF是平行四边形.
15.【解析】(1)因为CE=CD,点F为CE的中点,CF=2,所以DC=CE=2CF=4,因为四边形ABCD是平行四边形,所以AB=CD=4,,,在RtABE中,由勾股定理得
(2)证明:过G作GMAE于M,,
因为在DCF和ECG中,,,
,,即G为CD中点,,所以.M为AE中点,,,,
,,
_21?????????è?????(www.21cnjy.com)_
