人教版数学七年级下册5.2.1 平行线 课件(20张ppt)
文档属性
| 名称 | 人教版数学七年级下册5.2.1 平行线 课件(20张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-19 22:06:54 | ||
图片预览







文档简介
课件20张PPT。5.2 平行线及其判定
5.2.1 平行线人教版数学七年级下册1.了解平行线的概念,知道同一平面内不重合的两条直线的两种位置关系, 能叙述平行公理以及平行公理的推论.
2.会用符号语言表示平行公理及其推论, 会用三角尺和直尺过已知直线外一点画这条直线的平行线.学习目标如图,直线 a、b 是铁路上的两条铁轨,它们会相交吗?今天我们就来研究这样的两条直线——平行线.新课导入平行线分别将木条 a,b 与木条 c 钉在一起,并把它们想象成在同一平面内两端可以无限延伸的三条直线, 顺时针转动 a .
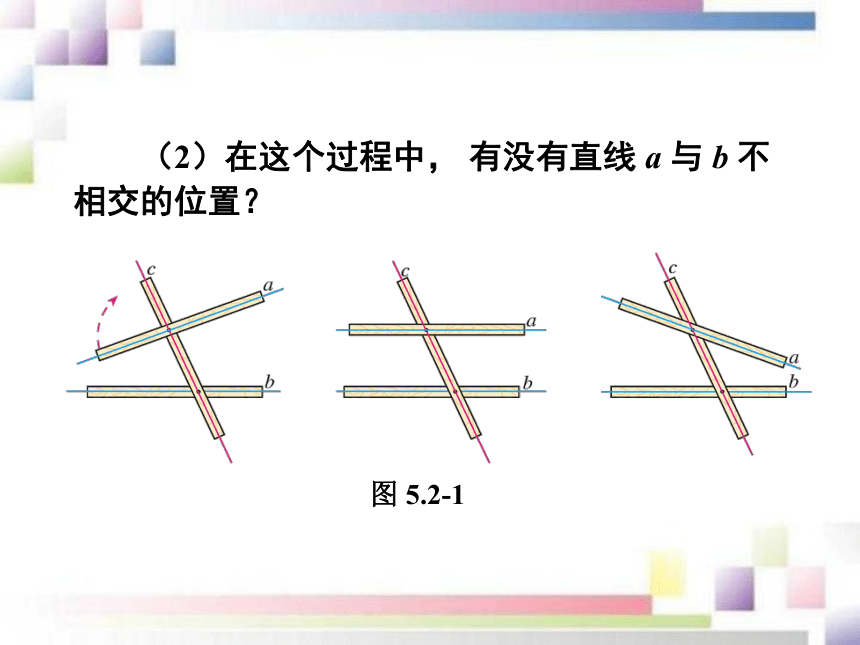
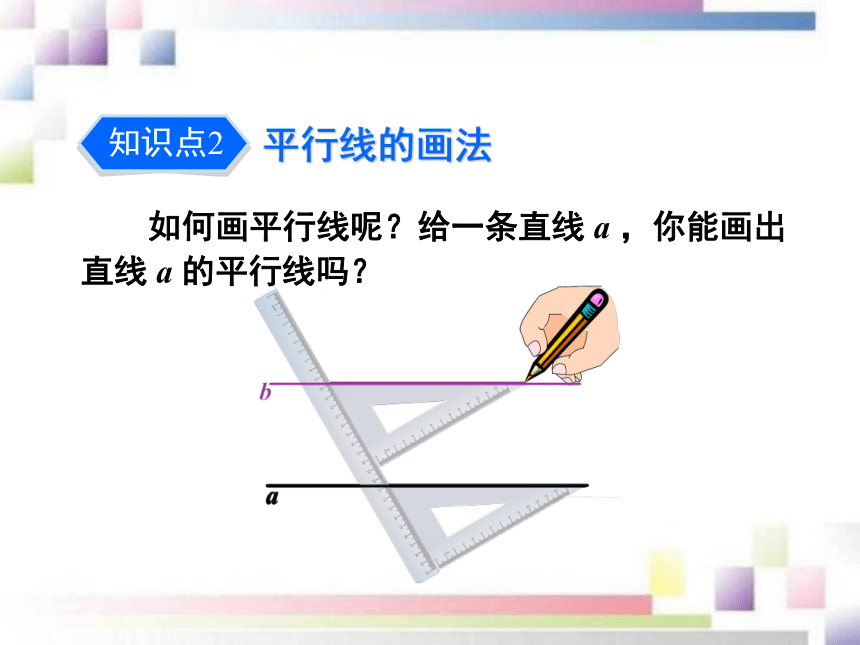
(1)直线 a 与直线 b 的交点位置将发生什么变化?新课导入(2)在这个过程中, 有没有直线 a 与 b 不相交的位置?图 5.2-1平行概念:同一平面内,存在一条直线 a与直线 b 不相交的位置,这时直线 a 与 b互相平行.换言之, 同一平面内, 不相交的两条直线叫做平行线.直线 a 与 b 是平行线, 记作 a∥b.同一平面内,不重合的两条直线存在哪些位置关系?相交和平行平行线在生活中很常见, 你能举出一些例子吗?图 5.2-2如何画平行线呢?给一条直线 a ,你能画出直线 a 的平行线吗?平行线的画法平行公理及其推论在图 5.2-1 转动木条 a 的过程中,有几个位置使得直线 a 与 b 平行? 如图5.2-3,过点 B 画直线 a 的平行线,能画出几条?再过点 C 画直线 a 的平行线,它和前面过点 B 画出的直线平行吗?图 5.2-3平行公理:经过直线外一点,有且只有一条直线与这条直线平行.平行公理推论:如果两条直线都与第三条直线平行,那么这两条直线也互相平行.如果b∥a,c∥a,那么b∥c. 读下列语句,并画出图形.
(1)点 P 是直线 AB 外一点,直线 CD 经过点 P,且与直线 AB 平行.即学即练读下列语句,并画出图形.
(2)直线 AB 与 CD 相交,点 P 是直线 AB、CD 外一点,直线 EF 经过点 P 且与直线 AB 平行,与直线 CD 相交于点 E .FE1. 在同一平面内,两条相交直线不可能都与第三条直线平行,这是因为__________________
________________________________________. 如果两条直线与第三条直线平行,那么这两条直线也互相平行随堂练习2.判断:
(1)不相交的两条直线叫做平行线. ( )
(2)如果一条直线与两条平行线中的一条平行, 那么它与另一条直线也互相平行. ( )
(3)过一点有且只有一条直线平行于已知直线. ( )√××点可能在已知直线上两条直线重合3.如图,若AB∥CD,经过点 E 可画EF∥AB,则 EF 与 CD 的位置关系是____________,理由是____________________________________________________________________.EF∥CD如果两条直线都与第三条直线平行,那么这两条直线也互相平行4.如图,MN⊥AB,垂足为
M,MN 交 CD 于点 N,过 M
点作 MG ⊥ CD ,垂足为 G ,
EF 过点N,且EF∥AB,交 MG 于点 H ,其中线段 GM 的长度是_______到_______的距离, 线段 MN 的长度是_______到_______的距离,又是___
_________________________的距离,点 N 到直线 MG 的距离是_______.点 MCD点 NAB两平行线 AB 与 EF 之间NG平行线平行线的定义和画法平行公理及其推导定义
画法平行公理
推论一落;二靠;三移;四画如果b∥a,c∥a,那么b∥c. 课堂小结谢谢!
5.2.1 平行线人教版数学七年级下册1.了解平行线的概念,知道同一平面内不重合的两条直线的两种位置关系, 能叙述平行公理以及平行公理的推论.
2.会用符号语言表示平行公理及其推论, 会用三角尺和直尺过已知直线外一点画这条直线的平行线.学习目标如图,直线 a、b 是铁路上的两条铁轨,它们会相交吗?今天我们就来研究这样的两条直线——平行线.新课导入平行线分别将木条 a,b 与木条 c 钉在一起,并把它们想象成在同一平面内两端可以无限延伸的三条直线, 顺时针转动 a .
(1)直线 a 与直线 b 的交点位置将发生什么变化?新课导入(2)在这个过程中, 有没有直线 a 与 b 不相交的位置?图 5.2-1平行概念:同一平面内,存在一条直线 a与直线 b 不相交的位置,这时直线 a 与 b互相平行.换言之, 同一平面内, 不相交的两条直线叫做平行线.直线 a 与 b 是平行线, 记作 a∥b.同一平面内,不重合的两条直线存在哪些位置关系?相交和平行平行线在生活中很常见, 你能举出一些例子吗?图 5.2-2如何画平行线呢?给一条直线 a ,你能画出直线 a 的平行线吗?平行线的画法平行公理及其推论在图 5.2-1 转动木条 a 的过程中,有几个位置使得直线 a 与 b 平行? 如图5.2-3,过点 B 画直线 a 的平行线,能画出几条?再过点 C 画直线 a 的平行线,它和前面过点 B 画出的直线平行吗?图 5.2-3平行公理:经过直线外一点,有且只有一条直线与这条直线平行.平行公理推论:如果两条直线都与第三条直线平行,那么这两条直线也互相平行.如果b∥a,c∥a,那么b∥c. 读下列语句,并画出图形.
(1)点 P 是直线 AB 外一点,直线 CD 经过点 P,且与直线 AB 平行.即学即练读下列语句,并画出图形.
(2)直线 AB 与 CD 相交,点 P 是直线 AB、CD 外一点,直线 EF 经过点 P 且与直线 AB 平行,与直线 CD 相交于点 E .FE1. 在同一平面内,两条相交直线不可能都与第三条直线平行,这是因为__________________
________________________________________. 如果两条直线与第三条直线平行,那么这两条直线也互相平行随堂练习2.判断:
(1)不相交的两条直线叫做平行线. ( )
(2)如果一条直线与两条平行线中的一条平行, 那么它与另一条直线也互相平行. ( )
(3)过一点有且只有一条直线平行于已知直线. ( )√××点可能在已知直线上两条直线重合3.如图,若AB∥CD,经过点 E 可画EF∥AB,则 EF 与 CD 的位置关系是____________,理由是____________________________________________________________________.EF∥CD如果两条直线都与第三条直线平行,那么这两条直线也互相平行4.如图,MN⊥AB,垂足为
M,MN 交 CD 于点 N,过 M
点作 MG ⊥ CD ,垂足为 G ,
EF 过点N,且EF∥AB,交 MG 于点 H ,其中线段 GM 的长度是_______到_______的距离, 线段 MN 的长度是_______到_______的距离,又是___
_________________________的距离,点 N 到直线 MG 的距离是_______.点 MCD点 NAB两平行线 AB 与 EF 之间NG平行线平行线的定义和画法平行公理及其推导定义
画法平行公理
推论一落;二靠;三移;四画如果b∥a,c∥a,那么b∥c. 课堂小结谢谢!
