人教版数学七年级下册5.2.2 平行线的判定 课件(31张ppt)
文档属性
| 名称 | 人教版数学七年级下册5.2.2 平行线的判定 课件(31张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-19 21:44:56 | ||
图片预览










文档简介
课件31张PPT。5.2.2 平行线的判定人教版数学七年级下册1.学会并记住平行线的判定方法1、2、3.
2.能运用平行线的判定方法进行简单的推理论证.学习目标上节课我们学习了平行线的概念和画法,这节课我们来研究如何判定两条直线是不是平行线.新课导入 如何判断两条直线是否平行?
(1) 根据定义.
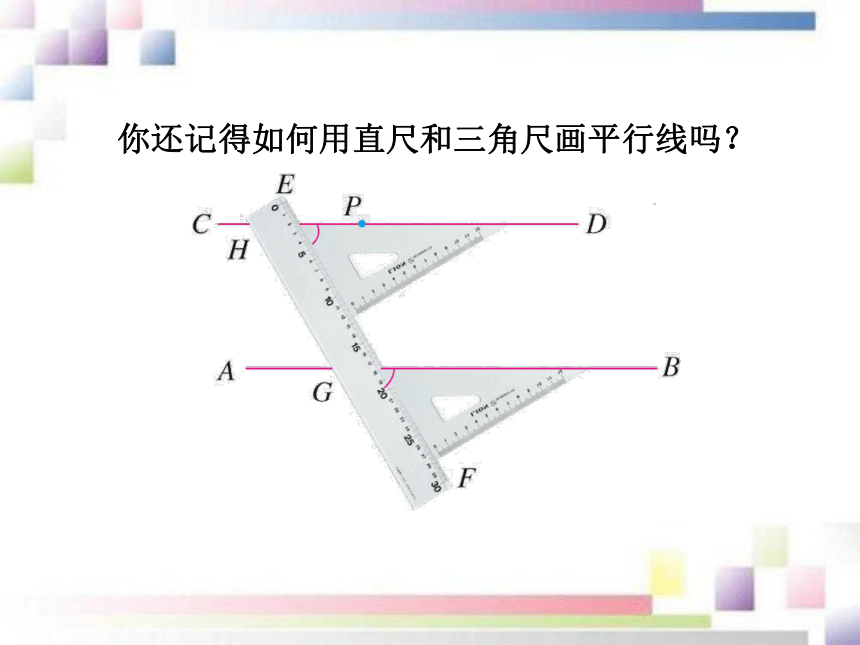
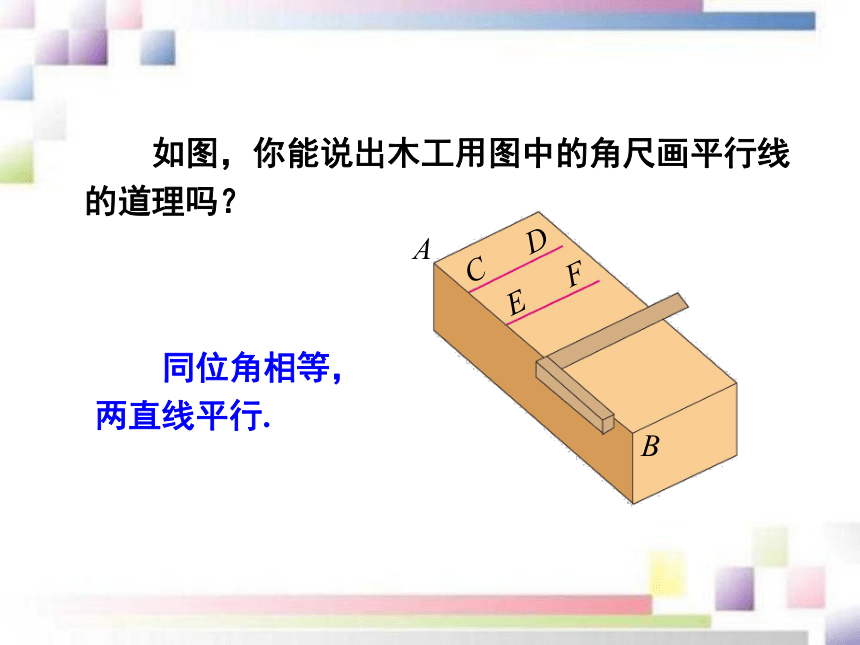
(2) 根据平行公理的推论.平行线的判定方法1、2、3知识讲解你还记得如何用直尺和三角尺画平行线吗?判定方法1 两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.简单说成:同位角相等,两直线平行.∠1 =∠2简化同位角相等,两直线平行.如图,你能说出木工用图中的角尺画平行线的道理吗?如果两条直线被第三条直线所截,那么能否利用内错角来判定两条直线平行呢?如图,如果∠2=∠3,那么 a 与 b 平行吗?因为∠2=∠3,∠3=∠1,
所以∠1=∠2,
所以 a∥b .判定方法2 两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.简单说成:内错角相等,两直线平行.如果两条直线被第三条直线所截,那么能否利用同旁内角来判定两条直线平行呢?如图,如果∠2+∠4=180°,那么a与b平行吗?因为∠2+∠4=180°,
∠1+∠4=180°,
所以∠1=∠2,
所以 a∥b .判定方法3 两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.简单说成:同旁内角互补,两直线平行.判定方法1 同位角相等,两直线平行.
判定方法2 内错角相等,两直线平行.
判定方法3 同旁内角互补,两直线平行.平行线的判定例 在同一平面内,如果两条直线都垂直于同一条直线,那么两条直线平行吗?为什么? 同一平面内,同垂直于第三条直线的两直线平行已知条件:直线 b 与直线 c 都垂直于直线 a .
要说明的结论:直线 b 与直线 c 平行吗?解:直线 b 与直线 c 平行.理由如下:
∵ b⊥a,∴ ∠1= 90°.
同理∠2= 90°.
∴ ∠1=∠2.
∵ ∠1和∠2是同位角,
∴ b∥c(同位角相等,两直线平行).你还能用其他方法说明理由吗?1. 如图, BE 是 AB 的延长线.
(1)由∠CBE =∠A 可以判定哪两条直线平行?根据是什么?答: AD∥BC . 根据同位角相等,两直线平行.随堂练习(2)由∠CBE =∠C 可以判定哪两条直线平行?根据是什么?答: AE∥CD . 根据内错角相等,两直线平行.答: AE∥CD . 根据同旁内角互补,两直线平行.(3)由∠D +∠A = 180°可以判定哪两条直线平行?根据是什么?2. 在铺设铁轨时,两条直轨必须是互相平行的.如图,已经知道∠2是直角,那么再度量图中已标出的哪个角,就可以判断两条直轨是否平行?为什么? 解:①可度量∠3的度数,因为∠3与∠2是同旁内角,若∠3=90°,则∠3+∠2=180°.根据“同旁内角互补,两直线平行”可得两条直轨平行.②也可度量∠4的度数,因为∠4与∠2是同位角,若∠4=90°,则∠4=∠2.根据“同位角相等,两直线平行”可得两条直轨平行.③还可度量∠5的度数,因为∠5与∠2是内错角,若∠5=90°,则∠5=∠2.根据“内错角相等,两直线平行”可得两条直轨平行.3.如图,这是小明同学自己制作的英语抄写纸的一部分,其中的横线互相平行吗?你有多少种判别方法?答:平行 . 理由不唯一.1. 如图,直线 a,b,c 被直线 l 所截,量得∠1=∠2=∠3.
(1)若∠1=∠2,则_____∥_____,理由是_________________________.ab同位角相等,两直线平行随堂练习(2)若∠1=∠3,则_____∥_____,理由是_________________________.
(3)直线 a,b,c 互相平行吗?为什么?ac内错角相等,两直线平行解:平行,∵ b∥a ,c∥a ,
∴ b∥c ,∴ a∥b∥c .2. 如图,如果∠2 =∠6,那么_____∥_____,如果∠3 + ∠4 + ∠5 + ∠6 = 180°, 那么______
∥______;如果∠9 =∠______,那么AD∥BC;如果∠9 =__________,那么AB∥CD.ADBCADBCDAB∠3 +∠43.如图,当∠1=∠3时,直线a,b平行吗?当∠2+∠3=180°时,直线a,b平行吗?为什么?解:∵∠1=∠3,∠3=∠4,
∴∠1=∠4,
∴a∥b(同位角相等,两直线平行).
∵∠3=∠4,∠2=∠5,∠2+∠3=180°,
∴∠4+∠5=180°,
∴a∥b(同旁内角互补,两直线平行).4.如图所示,已知直线 a,b,c,d,e,且∠1 = ∠2,∠3 + ∠4 = 180°,则 a 与 c 平行吗?为什么?解:∵∠1=∠2,
∴ a∥b(内错角相等,两直线平行).拓展练习∵∠3 + ∠4 = 180°,
∴b∥c(同旁内角互补,两直线平行).
又∵ a∥b,
∴ a∥c(如果两条直线都与第三条直线平行,那么这两条直线也互相平行).平行线的判定①平行公理的推论:如果两条直线都与第三条直线平行,这两条直线也互相平行.
②判定方法1:同位角相等,两直线平行.
③判定方法2:内错角相等,两直线平行.
④判定方法3:同旁内角互补,两直线平行.
⑤同一平面内,垂直于同一直线的两条直线平行.应用:判定生活中的平行线课堂小结谢谢!
2.能运用平行线的判定方法进行简单的推理论证.学习目标上节课我们学习了平行线的概念和画法,这节课我们来研究如何判定两条直线是不是平行线.新课导入 如何判断两条直线是否平行?
(1) 根据定义.
(2) 根据平行公理的推论.平行线的判定方法1、2、3知识讲解你还记得如何用直尺和三角尺画平行线吗?判定方法1 两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.简单说成:同位角相等,两直线平行.∠1 =∠2简化同位角相等,两直线平行.如图,你能说出木工用图中的角尺画平行线的道理吗?如果两条直线被第三条直线所截,那么能否利用内错角来判定两条直线平行呢?如图,如果∠2=∠3,那么 a 与 b 平行吗?因为∠2=∠3,∠3=∠1,
所以∠1=∠2,
所以 a∥b .判定方法2 两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.简单说成:内错角相等,两直线平行.如果两条直线被第三条直线所截,那么能否利用同旁内角来判定两条直线平行呢?如图,如果∠2+∠4=180°,那么a与b平行吗?因为∠2+∠4=180°,
∠1+∠4=180°,
所以∠1=∠2,
所以 a∥b .判定方法3 两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.简单说成:同旁内角互补,两直线平行.判定方法1 同位角相等,两直线平行.
判定方法2 内错角相等,两直线平行.
判定方法3 同旁内角互补,两直线平行.平行线的判定例 在同一平面内,如果两条直线都垂直于同一条直线,那么两条直线平行吗?为什么? 同一平面内,同垂直于第三条直线的两直线平行已知条件:直线 b 与直线 c 都垂直于直线 a .
要说明的结论:直线 b 与直线 c 平行吗?解:直线 b 与直线 c 平行.理由如下:
∵ b⊥a,∴ ∠1= 90°.
同理∠2= 90°.
∴ ∠1=∠2.
∵ ∠1和∠2是同位角,
∴ b∥c(同位角相等,两直线平行).你还能用其他方法说明理由吗?1. 如图, BE 是 AB 的延长线.
(1)由∠CBE =∠A 可以判定哪两条直线平行?根据是什么?答: AD∥BC . 根据同位角相等,两直线平行.随堂练习(2)由∠CBE =∠C 可以判定哪两条直线平行?根据是什么?答: AE∥CD . 根据内错角相等,两直线平行.答: AE∥CD . 根据同旁内角互补,两直线平行.(3)由∠D +∠A = 180°可以判定哪两条直线平行?根据是什么?2. 在铺设铁轨时,两条直轨必须是互相平行的.如图,已经知道∠2是直角,那么再度量图中已标出的哪个角,就可以判断两条直轨是否平行?为什么? 解:①可度量∠3的度数,因为∠3与∠2是同旁内角,若∠3=90°,则∠3+∠2=180°.根据“同旁内角互补,两直线平行”可得两条直轨平行.②也可度量∠4的度数,因为∠4与∠2是同位角,若∠4=90°,则∠4=∠2.根据“同位角相等,两直线平行”可得两条直轨平行.③还可度量∠5的度数,因为∠5与∠2是内错角,若∠5=90°,则∠5=∠2.根据“内错角相等,两直线平行”可得两条直轨平行.3.如图,这是小明同学自己制作的英语抄写纸的一部分,其中的横线互相平行吗?你有多少种判别方法?答:平行 . 理由不唯一.1. 如图,直线 a,b,c 被直线 l 所截,量得∠1=∠2=∠3.
(1)若∠1=∠2,则_____∥_____,理由是_________________________.ab同位角相等,两直线平行随堂练习(2)若∠1=∠3,则_____∥_____,理由是_________________________.
(3)直线 a,b,c 互相平行吗?为什么?ac内错角相等,两直线平行解:平行,∵ b∥a ,c∥a ,
∴ b∥c ,∴ a∥b∥c .2. 如图,如果∠2 =∠6,那么_____∥_____,如果∠3 + ∠4 + ∠5 + ∠6 = 180°, 那么______
∥______;如果∠9 =∠______,那么AD∥BC;如果∠9 =__________,那么AB∥CD.ADBCADBCDAB∠3 +∠43.如图,当∠1=∠3时,直线a,b平行吗?当∠2+∠3=180°时,直线a,b平行吗?为什么?解:∵∠1=∠3,∠3=∠4,
∴∠1=∠4,
∴a∥b(同位角相等,两直线平行).
∵∠3=∠4,∠2=∠5,∠2+∠3=180°,
∴∠4+∠5=180°,
∴a∥b(同旁内角互补,两直线平行).4.如图所示,已知直线 a,b,c,d,e,且∠1 = ∠2,∠3 + ∠4 = 180°,则 a 与 c 平行吗?为什么?解:∵∠1=∠2,
∴ a∥b(内错角相等,两直线平行).拓展练习∵∠3 + ∠4 = 180°,
∴b∥c(同旁内角互补,两直线平行).
又∵ a∥b,
∴ a∥c(如果两条直线都与第三条直线平行,那么这两条直线也互相平行).平行线的判定①平行公理的推论:如果两条直线都与第三条直线平行,这两条直线也互相平行.
②判定方法1:同位角相等,两直线平行.
③判定方法2:内错角相等,两直线平行.
④判定方法3:同旁内角互补,两直线平行.
⑤同一平面内,垂直于同一直线的两条直线平行.应用:判定生活中的平行线课堂小结谢谢!
