2020沪科版数学九年级下册第25章投影与视图单元综合卷(解析版)
文档属性
| 名称 | 2020沪科版数学九年级下册第25章投影与视图单元综合卷(解析版) |
|
|
| 格式 | zip | ||
| 文件大小 | 869.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-19 00:00:00 | ||
图片预览



文档简介
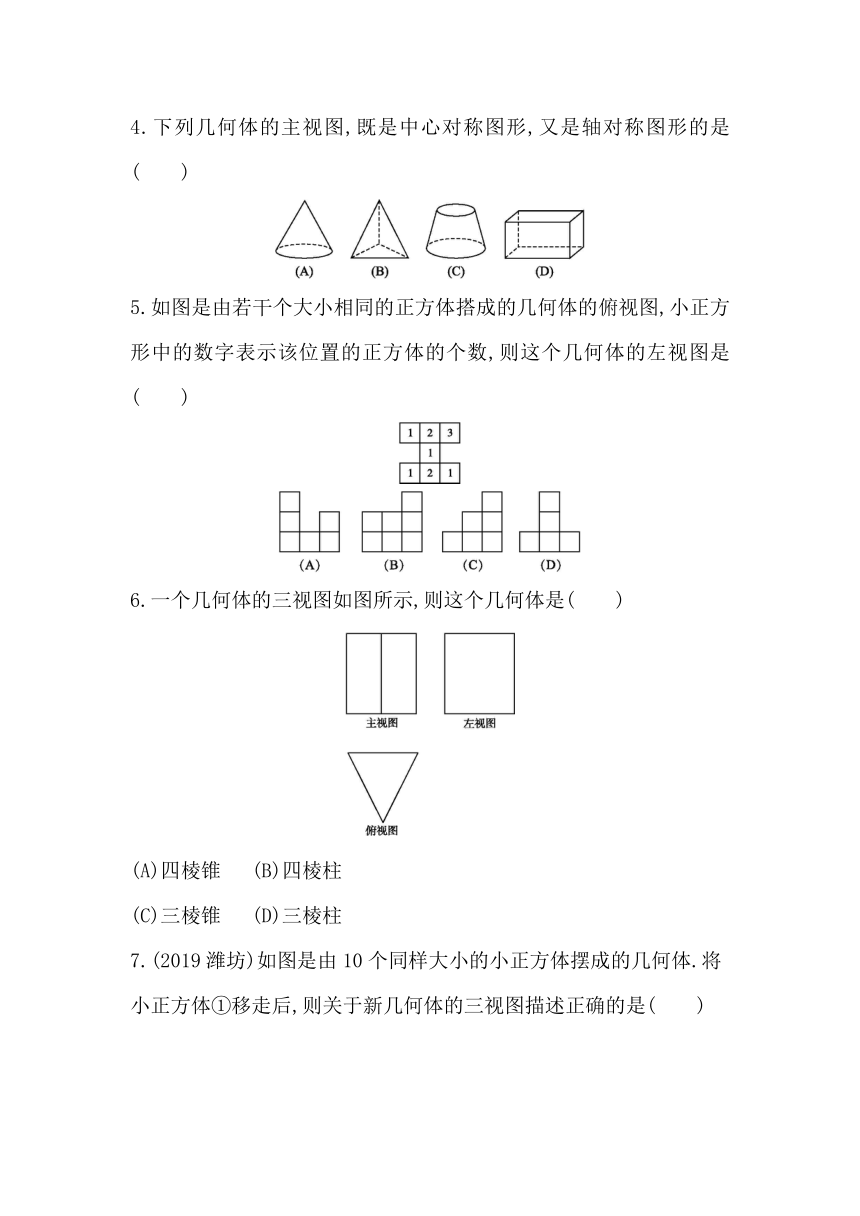
第25章 章末测试卷
(时间:45分钟 满分:100分)
一、选择题(每小题3分,共30分)
1.移动台阶如图所示,它的主视图是( )
2.在同一时刻的太阳光下,小刚的影子比小红的影子长,那么,在晚上同一路灯下,( )
(A)小刚的影子比小红的长
(B)小刚的影子比小红的影子短
(C)小刚跟小红的影子一样长
(D)不能够确定谁的影子长
3.如图是底面为正方形的长方体,下面有关它的三个视图的说法正确的是( )
(A)俯视图与主视图相同
(B)左视图与主视图相同
(C)左视图与俯视图相同
(D)三个视图都相同
4.下列几何体的主视图,既是中心对称图形,又是轴对称图形的是
( )
5.如图是由若干个大小相同的正方体搭成的几何体的俯视图,小正方形中的数字表示该位置的正方体的个数,则这个几何体的左视图是
( )
6.一个几何体的三视图如图所示,则这个几何体是( )
(A)四棱锥 (B)四棱柱
(C)三棱锥 (D)三棱柱
7.(2019潍坊)如图是由10个同样大小的小正方体摆成的几何体.将小正方体①移走后,则关于新几何体的三视图描述正确的是( )
(A)俯视图不变,左视图不变
(B)主视图改变,左视图改变
(C)俯视图不变,主视图不变
(D)主视图改变,俯视图改变
8.如图是三个大小不等的正方体拼成的几何体,其中两个较小正方体的棱长之和等于大正方体的棱长.该几何体的主视图、俯视图和左视图的面积分别是S1,S2,S3,则S1,S2,S3的大小关系是( )
(A)S1>S2>S3 (B)S3>S2>S1
(C)S2>S3>S1 (D)S1>S3>S2
9.如图是一个立体图形的两个视图,根据图示数据求出这个立体图形的体积是( )
(A)24π cm3 (B)48π cm3
(C)72π cm3 (D)192π cm3
10.如图,太阳光线与地面成60°的角,照在地面的一只排球上,排球在地面的投影长是14 cm,则排球的直径是( )
(A)7 cm (B)14 cm
(C)21 cm (D)21 cm
二、填空题(每小题4分,共24分)
11.请指出下列小明的影子中,平行投影是 ,中心投影是 .?
①一个晴天的上午,小明身后的影子;
②一个晴天的中午,小明脚下的影子;
③夜晚,小明在路灯下的影子;
④小明在幻灯机前经过时投在屏幕上的影子.
12.如图,是由27个相同的小立方块搭成的几何体,它的三个视图都是3×3的正方形,若拿掉若干个小立方块(几何体不倒掉),其三个视图仍都为3×3的正方形,则最多能拿掉小立方块的个数为 .?
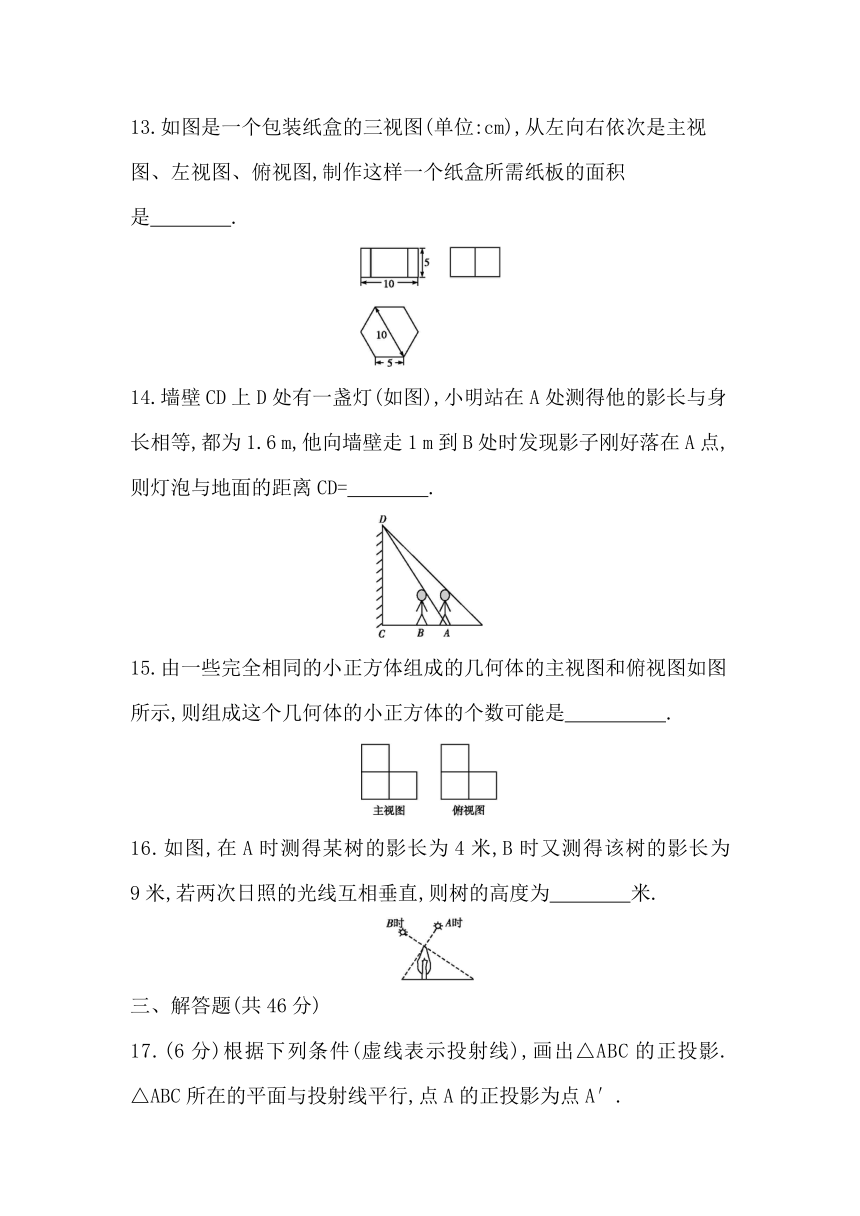
13.如图是一个包装纸盒的三视图(单位:cm),从左向右依次是主视图、左视图、俯视图,制作这样一个纸盒所需纸板的面积是 .?
14.墙壁CD上D处有一盏灯(如图),小明站在A处测得他的影长与身长相等,都为1.6 m,他向墙壁走1 m到B处时发现影子刚好落在A点,则灯泡与地面的距离CD= .?
15.由一些完全相同的小正方体组成的几何体的主视图和俯视图如图所示,则组成这个几何体的小正方体的个数可能是 .?
16.如图,在A时测得某树的影长为4米,B时又测得该树的影长为
9米,若两次日照的光线互相垂直,则树的高度为 米.?
三、解答题(共46分)
17.(6分)根据下列条件(虚线表示投射线),画出△ABC的正投影.
△ABC所在的平面与投射线平行,点A的正投影为点A′.
18.(6分)如图所示,楼房和旗杆在路灯下的影子如图所示,试确定路灯灯泡的位置,再作出小树在路灯下的影子.(不写作法,保留作图
痕迹)
19.(6分)(1)如图是由10个同样大小的小正方体搭成的几何体,请分别画出它的主视图和俯视图;
(2)在主视图和俯视图不变的情况下,你认为最多还可以添加 个小正方体.?
20.(9分)某工厂要加工一批茶叶罐,设计者给出了茶叶罐的三视图,如图,请你按照三视图确定制作每个茶叶罐所需铁皮的面积.(单位:毫米)
21.(9分)几何体的三视图相互关联.已知一直三棱柱及其三视图如图,在△PMN中,∠MPN=90°,PN=4,sin∠PMN=.
(1)求BC的长;
(2)若主视图与左视图两矩形相似,求AB的长;
(3)在(2)的情况下,求直三棱柱的表面积.
22.(10分)小颖、小华和小林想测量小区门口路灯的高度.如图,相邻的两盏路灯AC,BD高度相等,某天晚上,小颖站在E点处,此时她身后的影子的顶部刚好接触到路灯AC的底部;小华站在F点处,此时他身后影子的顶部刚好接触到路灯BD的底部.这时,小林测得EF=10.2米,已知AB=20米,小颖身高ME=1.6米,小华身高NF=1.7米,AC,BD,ME,NF均与地面垂直.请你根据以上数据计算路灯的高度.(结果精确到
0.1米)
附加题(共20分)
23.(10分)一个几何体的三视图如图所示,它的俯视图为菱形.请写出该几何体的形状,并根据图中所给的数据求出它的侧面积.
24.(10分)如图所示,点P表示广场上的一盏照明灯.
(1)请你在图中画出小敏在照明灯P照射下的影子(用线段表示);
(2)若小丽到灯柱MO的距离为4.5米,照明灯P到灯柱的距离为
1.5米,小丽目测照明灯P的仰角为55°,她的身高QB为1.6米,试求照明灯P到地面的距离(结果精确到0.1米).
(参考数据:tan 55°≈1.428,sin 55°≈0.819,cos 55°≈0.574)
第25章 章末测试卷
【测控导航表】
知识点 题号
投影 2,10,11,14,16,17,18,22
三视图的定义与画法 1,4,5,7,8,19
柱体的三视图 3,6
三视图的综合应用 8,9,12,13,15,20,21
一、选择题
1.B
2.D 解析:在同一路灯下由于位置不同,影长也不同,所以无法判断谁的影子长.故选D.
3.B 解析:俯视图是一个正方形,主视图和左视图都是一个长方形,且两个长方形的长和宽分别相等,所以B正确,故选B.
4.D 解析:A.主视图是等腰三角形,是轴对称图形,不是中心对称图形,故错误;
B.主视图是等腰三角形,是轴对称图形,不是中心对称图形,故错误;
C.主视图是等腰梯形,是轴对称图形,不是中心对称图形,故错误;
D.主视图是矩形,是轴对称图形,也是中心对称图形,故正确.故选D.
5.A 解析:从左边看有3列,第一列有3个正方形,第二列有1个正方形,第三列有2个正方形,故选A.
6.D 解析:由主视图和左视图为长方形,可得此几何体为柱体,
由俯视图为三角形,可得这个几何体是三棱柱.故选D.
7.A 解析:将正方体①移走后,
新几何体的三视图与原几何体的三视图相比,俯视图和左视图没有发生改变;
故选A.
8.D 解析:主视图的面积是三个正方形的面积和,左视图是两个较大的正方形的面积和,俯视图是大正方形的面积,故S1>S3>S2,故选D.
9.B 解析:易得该几何体为圆锥,底面圆的直径为8 cm,高为9 cm,则立体图形的体积为×π×()2×9=48π(cm3).故选B.
10.C 解析:如图,点A与点B为太阳光线与排球的切点,
则AB为排球的直径,CD=AB,DE=14 cm,
在Rt△CDE中,sin E=,
所以CD=14·sin 60°=14×=21(cm),
即排球的直径为21 cm.
故选C.
二、填空题
11.①② ③④ 解析:①和②都是太阳光形成的影子,是平行投影,③和④是灯光形成的影子,是中心投影.
12.12 解析:根据题意,拿掉若干个小立方块后,三个视图仍都为3×3的正方形,
则最多能拿掉小立方块的个数为6+6=12(个).
13.(150+75)cm2 解析:由三视图可知包装盒是一个正六棱柱,它的底面是正六边形,底面的面积为6××5×=(cm2),侧面积为6×52=150(cm2),
所以表面积为2×+150=(75+150)cm2.
即制作这样一个纸盒所需纸板的面积是(150+73)cm2.
14. m 解析:如图,根据题意得
BG=AF=AE=1.6 m,
AB=1 m,
因为BG∥AF∥CD,
所以△EAF∽△ECD,
△ABG∽△ACD,
所以AE∶CE=AF∶CD,AB∶AC=BG∶CD.
设BC=x m,CD=y m,
则CE=(x+2.6)m,AC=(x+1)m,
则即=,
解得x=,
把x=代入=,
解得y=,
所以CD= m.
15.4或5 解析:根据俯视图可知,该几何体底层有3个小正方体,根据主视图可知,该几何体上层左侧至少有1个小正方体,最多有2个小正方体.所以组成这个几何体的小正方体最少有4个,最多有5个.
16.6 解析:根据题意,作△EFC,如图,
树高为CD,且∠ECF=90°,ED=4,FD=9,
所以Rt△EDC∽Rt△CDF,
所以=,即CD2=ED·FD,
所以CD=6米.
三、解答题
17.解:如图所示.
18.解:点O就是路灯灯泡的位置,AB即为小树在路灯下的影子.
19.解:(1)如图所示.
(2)保持这个几何体的主视图和俯视图不变,可在左边最前面添加2个小正方体,左边中间添加1个小正方体,因此最多还可以添加3个小正方体.
20.解:由三视图可知茶叶罐的形状为圆柱体,并且茶叶罐的底面圆的直径2r为100毫米,
高h为150毫米,
因为每个茶叶罐所需铁皮的面积即为该圆柱体的表面积,
所以S表面积=2πr2+2πrh
=2π×502+2π×50×150
=20 000π(平方毫米).
答:制作每个茶叶罐所需铁皮的面积为20 000π平方毫米.
21.解:(1)由题图可知BC=MN,
因为sin∠PMN==,PN=4,
所以MN=5,
所以BC的长是5.
(2)因为矩形ABCD与矩形EFGH相似,
且AB=EF,
所以=,
在Rt△PMN中,PM==3,
设斜边MN上的高为h,
则FG=h==,
所以=,
所以AB=2,即AB的长为2.
(3)直三棱柱的表面积为
×3×4×2+2×3+2×4+2×5
=12+24.
22.解:设AE=x米,
则BF=(20-10.2-x)米,
因为ME∥BD,
所以△AME∽△ADB,
所以=,即=,
所以x=.
因为NF∥AC,所以△BNF∽△BCA,
所以=,即=,
所以x=9.8-,
所以=9.8-,
所以BD≈6.8米,
答:路灯的高度约为6.8米.
附加题
23.解:该几何体是直四棱柱,
由三视图知,棱柱底面菱形的对角线长分别为4 cm,3 cm,
所以菱形的边长为 cm,
故直四棱柱的侧面积为×8×4=80(cm2).
24.解:(1)如图,线段AC是小敏的影子.
(2)过点Q作QE⊥MO于E,
过点P作PF⊥AB于F,交EQ于点D,
则PF⊥EQ,
在Rt△PDQ中,∠PQD=55°,
DQ=EQ-ED=4.5-1.5=3(米),
因为tan 55°=,
所以PD=3tan 55°≈4.28(米),
因为DF=QB=1.6米,
所以PF=PD+DF≈4.28+1.6≈5.9(米).
答:照明灯P到地面的距离约为5.9米.
(时间:45分钟 满分:100分)
一、选择题(每小题3分,共30分)
1.移动台阶如图所示,它的主视图是( )
2.在同一时刻的太阳光下,小刚的影子比小红的影子长,那么,在晚上同一路灯下,( )
(A)小刚的影子比小红的长
(B)小刚的影子比小红的影子短
(C)小刚跟小红的影子一样长
(D)不能够确定谁的影子长
3.如图是底面为正方形的长方体,下面有关它的三个视图的说法正确的是( )
(A)俯视图与主视图相同
(B)左视图与主视图相同
(C)左视图与俯视图相同
(D)三个视图都相同
4.下列几何体的主视图,既是中心对称图形,又是轴对称图形的是
( )
5.如图是由若干个大小相同的正方体搭成的几何体的俯视图,小正方形中的数字表示该位置的正方体的个数,则这个几何体的左视图是
( )
6.一个几何体的三视图如图所示,则这个几何体是( )
(A)四棱锥 (B)四棱柱
(C)三棱锥 (D)三棱柱
7.(2019潍坊)如图是由10个同样大小的小正方体摆成的几何体.将小正方体①移走后,则关于新几何体的三视图描述正确的是( )
(A)俯视图不变,左视图不变
(B)主视图改变,左视图改变
(C)俯视图不变,主视图不变
(D)主视图改变,俯视图改变
8.如图是三个大小不等的正方体拼成的几何体,其中两个较小正方体的棱长之和等于大正方体的棱长.该几何体的主视图、俯视图和左视图的面积分别是S1,S2,S3,则S1,S2,S3的大小关系是( )
(A)S1>S2>S3 (B)S3>S2>S1
(C)S2>S3>S1 (D)S1>S3>S2
9.如图是一个立体图形的两个视图,根据图示数据求出这个立体图形的体积是( )
(A)24π cm3 (B)48π cm3
(C)72π cm3 (D)192π cm3
10.如图,太阳光线与地面成60°的角,照在地面的一只排球上,排球在地面的投影长是14 cm,则排球的直径是( )
(A)7 cm (B)14 cm
(C)21 cm (D)21 cm
二、填空题(每小题4分,共24分)
11.请指出下列小明的影子中,平行投影是 ,中心投影是 .?
①一个晴天的上午,小明身后的影子;
②一个晴天的中午,小明脚下的影子;
③夜晚,小明在路灯下的影子;
④小明在幻灯机前经过时投在屏幕上的影子.
12.如图,是由27个相同的小立方块搭成的几何体,它的三个视图都是3×3的正方形,若拿掉若干个小立方块(几何体不倒掉),其三个视图仍都为3×3的正方形,则最多能拿掉小立方块的个数为 .?
13.如图是一个包装纸盒的三视图(单位:cm),从左向右依次是主视图、左视图、俯视图,制作这样一个纸盒所需纸板的面积是 .?
14.墙壁CD上D处有一盏灯(如图),小明站在A处测得他的影长与身长相等,都为1.6 m,他向墙壁走1 m到B处时发现影子刚好落在A点,则灯泡与地面的距离CD= .?
15.由一些完全相同的小正方体组成的几何体的主视图和俯视图如图所示,则组成这个几何体的小正方体的个数可能是 .?
16.如图,在A时测得某树的影长为4米,B时又测得该树的影长为
9米,若两次日照的光线互相垂直,则树的高度为 米.?
三、解答题(共46分)
17.(6分)根据下列条件(虚线表示投射线),画出△ABC的正投影.
△ABC所在的平面与投射线平行,点A的正投影为点A′.
18.(6分)如图所示,楼房和旗杆在路灯下的影子如图所示,试确定路灯灯泡的位置,再作出小树在路灯下的影子.(不写作法,保留作图
痕迹)
19.(6分)(1)如图是由10个同样大小的小正方体搭成的几何体,请分别画出它的主视图和俯视图;
(2)在主视图和俯视图不变的情况下,你认为最多还可以添加 个小正方体.?
20.(9分)某工厂要加工一批茶叶罐,设计者给出了茶叶罐的三视图,如图,请你按照三视图确定制作每个茶叶罐所需铁皮的面积.(单位:毫米)
21.(9分)几何体的三视图相互关联.已知一直三棱柱及其三视图如图,在△PMN中,∠MPN=90°,PN=4,sin∠PMN=.
(1)求BC的长;
(2)若主视图与左视图两矩形相似,求AB的长;
(3)在(2)的情况下,求直三棱柱的表面积.
22.(10分)小颖、小华和小林想测量小区门口路灯的高度.如图,相邻的两盏路灯AC,BD高度相等,某天晚上,小颖站在E点处,此时她身后的影子的顶部刚好接触到路灯AC的底部;小华站在F点处,此时他身后影子的顶部刚好接触到路灯BD的底部.这时,小林测得EF=10.2米,已知AB=20米,小颖身高ME=1.6米,小华身高NF=1.7米,AC,BD,ME,NF均与地面垂直.请你根据以上数据计算路灯的高度.(结果精确到
0.1米)
附加题(共20分)
23.(10分)一个几何体的三视图如图所示,它的俯视图为菱形.请写出该几何体的形状,并根据图中所给的数据求出它的侧面积.
24.(10分)如图所示,点P表示广场上的一盏照明灯.
(1)请你在图中画出小敏在照明灯P照射下的影子(用线段表示);
(2)若小丽到灯柱MO的距离为4.5米,照明灯P到灯柱的距离为
1.5米,小丽目测照明灯P的仰角为55°,她的身高QB为1.6米,试求照明灯P到地面的距离(结果精确到0.1米).
(参考数据:tan 55°≈1.428,sin 55°≈0.819,cos 55°≈0.574)
第25章 章末测试卷
【测控导航表】
知识点 题号
投影 2,10,11,14,16,17,18,22
三视图的定义与画法 1,4,5,7,8,19
柱体的三视图 3,6
三视图的综合应用 8,9,12,13,15,20,21
一、选择题
1.B
2.D 解析:在同一路灯下由于位置不同,影长也不同,所以无法判断谁的影子长.故选D.
3.B 解析:俯视图是一个正方形,主视图和左视图都是一个长方形,且两个长方形的长和宽分别相等,所以B正确,故选B.
4.D 解析:A.主视图是等腰三角形,是轴对称图形,不是中心对称图形,故错误;
B.主视图是等腰三角形,是轴对称图形,不是中心对称图形,故错误;
C.主视图是等腰梯形,是轴对称图形,不是中心对称图形,故错误;
D.主视图是矩形,是轴对称图形,也是中心对称图形,故正确.故选D.
5.A 解析:从左边看有3列,第一列有3个正方形,第二列有1个正方形,第三列有2个正方形,故选A.
6.D 解析:由主视图和左视图为长方形,可得此几何体为柱体,
由俯视图为三角形,可得这个几何体是三棱柱.故选D.
7.A 解析:将正方体①移走后,
新几何体的三视图与原几何体的三视图相比,俯视图和左视图没有发生改变;
故选A.
8.D 解析:主视图的面积是三个正方形的面积和,左视图是两个较大的正方形的面积和,俯视图是大正方形的面积,故S1>S3>S2,故选D.
9.B 解析:易得该几何体为圆锥,底面圆的直径为8 cm,高为9 cm,则立体图形的体积为×π×()2×9=48π(cm3).故选B.
10.C 解析:如图,点A与点B为太阳光线与排球的切点,
则AB为排球的直径,CD=AB,DE=14 cm,
在Rt△CDE中,sin E=,
所以CD=14·sin 60°=14×=21(cm),
即排球的直径为21 cm.
故选C.
二、填空题
11.①② ③④ 解析:①和②都是太阳光形成的影子,是平行投影,③和④是灯光形成的影子,是中心投影.
12.12 解析:根据题意,拿掉若干个小立方块后,三个视图仍都为3×3的正方形,
则最多能拿掉小立方块的个数为6+6=12(个).
13.(150+75)cm2 解析:由三视图可知包装盒是一个正六棱柱,它的底面是正六边形,底面的面积为6××5×=(cm2),侧面积为6×52=150(cm2),
所以表面积为2×+150=(75+150)cm2.
即制作这样一个纸盒所需纸板的面积是(150+73)cm2.
14. m 解析:如图,根据题意得
BG=AF=AE=1.6 m,
AB=1 m,
因为BG∥AF∥CD,
所以△EAF∽△ECD,
△ABG∽△ACD,
所以AE∶CE=AF∶CD,AB∶AC=BG∶CD.
设BC=x m,CD=y m,
则CE=(x+2.6)m,AC=(x+1)m,
则即=,
解得x=,
把x=代入=,
解得y=,
所以CD= m.
15.4或5 解析:根据俯视图可知,该几何体底层有3个小正方体,根据主视图可知,该几何体上层左侧至少有1个小正方体,最多有2个小正方体.所以组成这个几何体的小正方体最少有4个,最多有5个.
16.6 解析:根据题意,作△EFC,如图,
树高为CD,且∠ECF=90°,ED=4,FD=9,
所以Rt△EDC∽Rt△CDF,
所以=,即CD2=ED·FD,
所以CD=6米.
三、解答题
17.解:如图所示.
18.解:点O就是路灯灯泡的位置,AB即为小树在路灯下的影子.
19.解:(1)如图所示.
(2)保持这个几何体的主视图和俯视图不变,可在左边最前面添加2个小正方体,左边中间添加1个小正方体,因此最多还可以添加3个小正方体.
20.解:由三视图可知茶叶罐的形状为圆柱体,并且茶叶罐的底面圆的直径2r为100毫米,
高h为150毫米,
因为每个茶叶罐所需铁皮的面积即为该圆柱体的表面积,
所以S表面积=2πr2+2πrh
=2π×502+2π×50×150
=20 000π(平方毫米).
答:制作每个茶叶罐所需铁皮的面积为20 000π平方毫米.
21.解:(1)由题图可知BC=MN,
因为sin∠PMN==,PN=4,
所以MN=5,
所以BC的长是5.
(2)因为矩形ABCD与矩形EFGH相似,
且AB=EF,
所以=,
在Rt△PMN中,PM==3,
设斜边MN上的高为h,
则FG=h==,
所以=,
所以AB=2,即AB的长为2.
(3)直三棱柱的表面积为
×3×4×2+2×3+2×4+2×5
=12+24.
22.解:设AE=x米,
则BF=(20-10.2-x)米,
因为ME∥BD,
所以△AME∽△ADB,
所以=,即=,
所以x=.
因为NF∥AC,所以△BNF∽△BCA,
所以=,即=,
所以x=9.8-,
所以=9.8-,
所以BD≈6.8米,
答:路灯的高度约为6.8米.
附加题
23.解:该几何体是直四棱柱,
由三视图知,棱柱底面菱形的对角线长分别为4 cm,3 cm,
所以菱形的边长为 cm,
故直四棱柱的侧面积为×8×4=80(cm2).
24.解:(1)如图,线段AC是小敏的影子.
(2)过点Q作QE⊥MO于E,
过点P作PF⊥AB于F,交EQ于点D,
则PF⊥EQ,
在Rt△PDQ中,∠PQD=55°,
DQ=EQ-ED=4.5-1.5=3(米),
因为tan 55°=,
所以PD=3tan 55°≈4.28(米),
因为DF=QB=1.6米,
所以PF=PD+DF≈4.28+1.6≈5.9(米).
答:照明灯P到地面的距离约为5.9米.
