2018-2019学年黑龙江省哈尔滨市香坊区旭东中学八年级(下)期中数学试卷(人教五四学制) 解析版
文档属性
| 名称 | 2018-2019学年黑龙江省哈尔滨市香坊区旭东中学八年级(下)期中数学试卷(人教五四学制) 解析版 |  | |
| 格式 | zip | ||
| 文件大小 | 515.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-19 23:25:00 | ||
图片预览



文档简介
2018-2019学年黑龙江省哈尔滨市香坊区旭东中学八年级(下)期中数学试卷(五四学制)
一.选择题(共10小题,满分30分)
1.下列方程中,属于一元二次方程的是( )
A.x+2y=1 B.ax2+bx+c=0 C.3x+=4 D.x2﹣2=0
2.直角三角形的两条直角边的长分别为6和8,则斜边长为( )
A.10 B.5 C.4 D.3
3.若a,b,c为三角形的三边,则下列各组数据中,不能组成直角三角形的是( )
A.a=8,b=15,c=17 B.a=3,b=5,c=4
C.a=4,b=8,c=9 D.a=9,b=40,c=41
4.已知?ABCD中,∠A+∠C=200°,则∠B的度数是( )
A.100° B.160° C.80° D.60°
5.下列说法错误的是( )
A.四个角都相等的四边形是矩形
B.三角形的中位线平行于三角形的第三边且等于第三边的一半
C.两条对角线相等的四边形是矩形
D.一组对边平行且一组对角相等的四边形是平行四边形
6.关于x的一元二次方程(a﹣1)x2+x+a2﹣1=0的一个根是0,则a的值为( )
A.1 B.﹣1 C.1或﹣1 D.0
7.关于x的一元二次方程x2﹣3x+m=0有两个不相等的实数根,则实数m的取值范围为( )
A.m≥ B.m< C.m= D.m<﹣
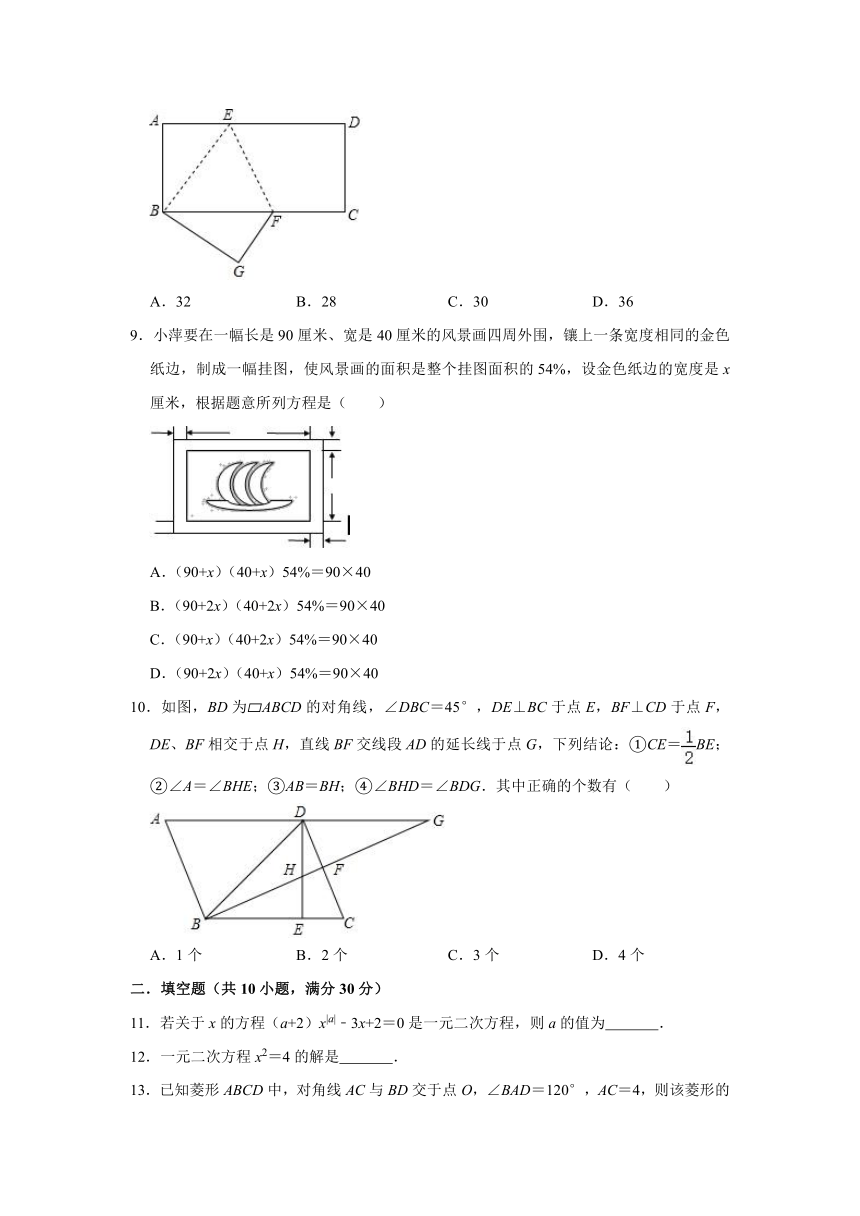
8.如图,将一边长AB为4的矩形纸片折叠,使点D与点B重合,折痕为EF,若EF=2,则矩形的面积为( )
A.32 B.28 C.30 D.36
9.小萍要在一幅长是90厘米、宽是40厘米的风景画四周外围,镶上一条宽度相同的金色纸边,制成一幅挂图,使风景画的面积是整个挂图面积的54%,设金色纸边的宽度是x厘米,根据题意所列方程是( )
A.(90+x)(40+x)54%=90×40
B.(90+2x)(40+2x)54%=90×40
C.(90+x)(40+2x)54%=90×40
D.(90+2x)(40+x)54%=90×40
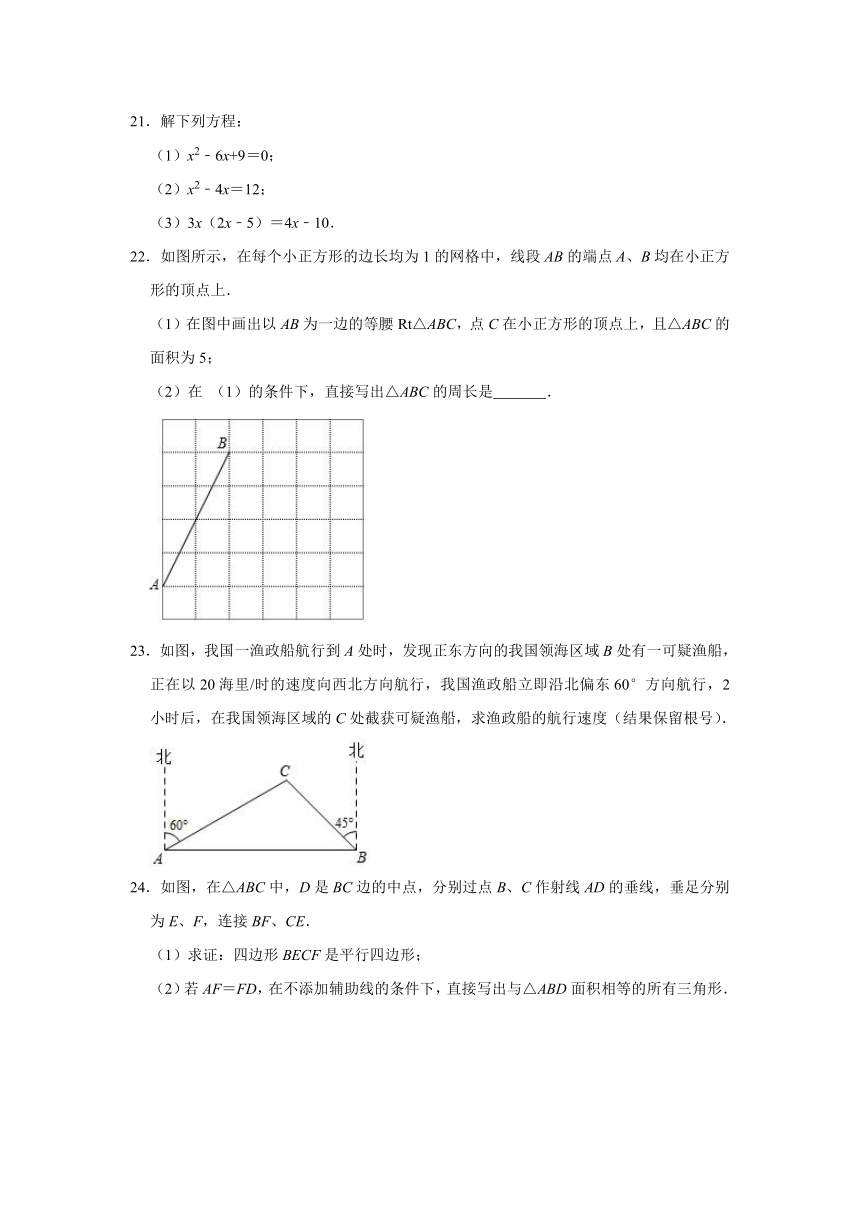
10.如图,BD为?ABCD的对角线,∠DBC=45°,DE⊥BC于点E,BF⊥CD于点F,DE、BF相交于点H,直线BF交线段AD的延长线于点G,下列结论:①CE=BE;②∠A=∠BHE;③AB=BH;④∠BHD=∠BDG.其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
二.填空题(共10小题,满分30分)
11.若关于x的方程(a+2)x|a|﹣3x+2=0是一元二次方程,则a的值为 .
12.一元二次方程x2=4的解是 .
13.已知菱形ABCD中,对角线AC与BD交于点O,∠BAD=120°,AC=4,则该菱形的面积是 .
14.Rt△ABC中,斜边AB上的高为CD,若AC=3,BC=4.则CD= .
15.如图,E为?ABCD外一点,且EB⊥BC,ED⊥CD,若∠E=65°,则∠A的度数为 .
16.某种服装平均每天可以销售20件,每件盈利32元,在每件降价幅度不超过10元的情况下,若每件降价1元,则每天可多售出5件,若每天要盈利900元,每件应降价 元.
17.有一个人患了流感,经过两轮传染后得知第二次被传染的有420人,如果每轮传染率都相同,那么每轮传染中平均一个人传染了 个人.
18.菱形ABCD中,∠A=60°,AB=9,点P是菱形ABCD内一点,PB=PD=3,则AP的长为 .
19.已知菱形ABCD的两条对角线分别为6和8,M、N分别是边BC、CD的中点,P是对角线BD上一点,则PM+PN的最小值= .
20.如图,在矩形ABCD中,BD为对角线,过点C作CE⊥BD,交AB于点E,点F在BC上,AF交CE于点G,且AG=GF=CF,BD=,则线段AB的长为 .
三.解答题(共7小题,满分60分)
21.解下列方程:
(1)x2﹣6x+9=0;
(2)x2﹣4x=12;
(3)3x(2x﹣5)=4x﹣10.
22.如图所示,在每个小正方形的边长均为1的网格中,线段AB的端点A、B均在小正方形的顶点上.
(1)在图中画出以AB为一边的等腰Rt△ABC,点C在小正方形的顶点上,且△ABC的面积为5;
(2)在 (1)的条件下,直接写出△ABC的周长是 .
23.如图,我国一渔政船航行到A处时,发现正东方向的我国领海区域B处有一可疑渔船,正在以20海里/时的速度向西北方向航行,我国渔政船立即沿北偏东60°方向航行,2小时后,在我国领海区域的C处截获可疑渔船,求渔政船的航行速度(结果保留根号).
24.如图,在△ABC中,D是BC边的中点,分别过点B、C作射线AD的垂线,垂足分别为E、F,连接BF、CE.
(1)求证:四边形BECF是平行四边形;
(2)若AF=FD,在不添加辅助线的条件下,直接写出与△ABD面积相等的所有三角形.
25.六一儿童节,某玩具经销商在销售中发现:某款玩具若以每个50元销售,一个月能售出500个,销售单价每涨1元,月销售量就减少10个,这款玩具的进价为每个40元,请回答以下问题:
(1)若月销售利润定为8000元,且尽可能让利消费者,销售单价应定为多少元?
(2)由于资金问题,在月销售成本不超过10000元、且没有库存积压的情况下,问销售单价至少定为多少元?
26.已知正方形ABCD,M是直线BC上的一点,过点B作BE⊥DM于点E,交直线CD于点F,过点F作FG∥BC交直线BD于点G.
(1)如图1,点M在线段BC上时,直接写出FG、MC、AD之间的数量关系 ;
(2)如图2,点M在线段BC的延长线上时,求证:FG+MC=BC;
(3)如图3,过点E作EN⊥BD于点N,连接AN,若S△EFD=DF2,AB=4,求AN的长.
27.如图,在平面直角坐标系中,点O为坐标原点,B(2,0),点A在y轴正半轴上,AB=2.
(1)直接写出A点坐标 ;
(2)将△AOB沿x轴正方向平移,得到△DEC,点A对应点D,点B对应点C,点O对应点E.连接AD,作∠BAD的平分线,交射线DC于点F,设E点的横坐标为t,线段CF的长为d,求d与t的关系式(不要求写出t的取值范围);
(3)在 (2)的条件下,当点F在线段DC上时,AF与DE交于点G,连接EF,若∠DFE﹣∠BAF=45°,求此时t的值,并判断坐标平面内是否存在一点M,使以点A、D、G、M为顶点的四边形是平行四边形?若存在,请求出点M的坐标;若不存在,请说明理由.
2018-2019学年黑龙江省哈尔滨市香坊区旭东中学八年级(下)期中数学试卷(五四学制)
参考答案与试题解析
一.选择题(共10小题)
1.下列方程中,属于一元二次方程的是( )
A.x+2y=1 B.ax2+bx+c=0 C.3x+=4 D.x2﹣2=0
【分析】首先判断是否是整式方程,如果是整式方程,化简后只含有一个未知数,未知数的最高次数是2,这样的方程就是一元二次方程.
【解答】解:A、含有2个未知数,故错误;
B、当a=0时不是一元二次方程,故错误;
C、为分式方程,故错误;
D、只含有一个未知数,未知数的最高次数是2,二次项系数不为0,是一元二次方程,正确;
故选:D.
2.直角三角形的两条直角边的长分别为6和8,则斜边长为( )
A.10 B.5 C.4 D.3
【分析】根据直角三角形的两条直角边的长为6和8,利用勾股定理即可求出其斜边的长.
【解答】解;∵直角三角形的两条直角边的长为6和8,
∴它的斜边长==10.
故选:A.
3.若a,b,c为三角形的三边,则下列各组数据中,不能组成直角三角形的是( )
A.a=8,b=15,c=17 B.a=3,b=5,c=4
C.a=4,b=8,c=9 D.a=9,b=40,c=41
【分析】欲判断能否构成直角三角形,只需验证两小边的平方和是否等于最长边的平方.
【解答】解:A、82+152=172,能构成直角三角形;
B、32+42=52,能构成直角三角形;
C、42+82≠92,不能构成直角三角形;
D、92+402=412,能构成直角三角形.
故选:C.
4.已知?ABCD中,∠A+∠C=200°,则∠B的度数是( )
A.100° B.160° C.80° D.60°
【分析】由四边形ABCD是平行四边形,可得∠A=∠C,AD∥BC,又由∠A+∠C=200°,即可求得∠A的度数,继而求得答案.
【解答】解:∵四边形ABCD是平行四边形,
∴∠A=∠C,AD∥BC,
∵∠A+∠C=200°,
∴∠A=100°,
∴∠B=180°﹣∠A=80°.
故选:C.
5.下列说法错误的是( )
A.四个角都相等的四边形是矩形
B.三角形的中位线平行于三角形的第三边且等于第三边的一半
C.两条对角线相等的四边形是矩形
D.一组对边平行且一组对角相等的四边形是平行四边形
【分析】根据矩形的判定、平行四边形的判定、三角形的中位线的性质等知识一一判断即可.
【解答】解:A、四个角都相等的四边形是矩形,正确.
B、三角形的中位线平行于三角形的第三边且等于第三边的一半,正确.
C、错误.对角线相等的四边形不一定是矩形.
D、一组对边平行且一组对角相等的四边形是平行四边形,正确.
故选:C.
6.关于x的一元二次方程(a﹣1)x2+x+a2﹣1=0的一个根是0,则a的值为( )
A.1 B.﹣1 C.1或﹣1 D.0
【分析】将x=0代入方程可得:a2﹣1=0,解之求得a的值,在根据一元二次方程的定义求解可得.
【解答】解:根据题意将x=0代入方程可得:a2﹣1=0,
解得:a=1或a=﹣1,
∵a﹣1≠0,即a≠1,
∴a=﹣1,
故选:B.
7.关于x的一元二次方程x2﹣3x+m=0有两个不相等的实数根,则实数m的取值范围为( )
A.m≥ B.m< C.m= D.m<﹣
【分析】若一元二次方程有两不等根,则根的判别式△=b2﹣4ac>0,建立关于m的不等式,求出m的取值范围.
【解答】解:∵方程有两个不相等的实数根,a=1,b=﹣3,c=m,
∴△=b2﹣4ac=(﹣3)2﹣4×1×m>0,
解得m<.
故选:B.
8.如图,将一边长AB为4的矩形纸片折叠,使点D与点B重合,折痕为EF,若EF=2,则矩形的面积为( )
A.32 B.28 C.30 D.36
【分析】连接BD交EF于O,由折叠的性质得出BD⊥EF,BO=DO,OE=OF=EF=,设BC=x,BD==,则BO=,易证△BOF∽△BCD,得出=,求出BC=8,即可得出结果.
【解答】解:连接BD交EF于O,如图所示:
∵折叠纸片使点D与点B重合,折痕为EF,
∴BD⊥EF,BO=DO,OE=OF=EF=,
∵四边形ABCD是矩形,
∴AB=CD=4,∠BCD=90°,
设BC=x,
BD==,
∴BO=,
∵∠BOF=∠C=90°,∠CBD=∠OBF,
∴△BOF∽△BCD,
∴=,
即:=,
解得:x=8,
∴BC=8,
∴S矩形ABCD=AB?BC=4×8=32,
故选:A.
9.小萍要在一幅长是90厘米、宽是40厘米的风景画四周外围,镶上一条宽度相同的金色纸边,制成一幅挂图,使风景画的面积是整个挂图面积的54%,设金色纸边的宽度是x厘米,根据题意所列方程是( )
A.(90+x)(40+x)54%=90×40
B.(90+2x)(40+2x)54%=90×40
C.(90+x)(40+2x)54%=90×40
D.(90+2x)(40+x)54%=90×40
【分析】本题可根据题意运用面积公式列出方程,再进行化简即可得出本题的答案.
【解答】解:依题意得:
(2x+90)(2x+40)×54%=90×40.
故选:B.
10.如图,BD为?ABCD的对角线,∠DBC=45°,DE⊥BC于点E,BF⊥CD于点F,DE、BF相交于点H,直线BF交线段AD的延长线于点G,下列结论:①CE=BE;②∠A=∠BHE;③AB=BH;④∠BHD=∠BDG.其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
【分析】通过判断△BDE为等腰直角三角形,得到BE=DE,根据等角的余角相等得到∠BHE=∠C,再根据平行四边形的性质得到∠A=∠C,则∠A=∠BHE,于是可对②进行判断;根据“AAS”可证明△BEH≌△DEC,得到BH=CD,CE=EH,可对①进行判断;接着由平行四边形的性质得AB=CD,则AB=BH,运算可对③进行判断;因为∠BDH=90°+∠EBH,∠BDG=90°+∠BDE,由∠BDE>∠EBH,推出∠BDG>∠BHD,所以④错误;
【解答】解:∵∠DBC=45°,DE⊥BC,
∴△BDE为等腰直角三角形,
∴BE=DE,
∵BF⊥CD,
∴∠C+∠CBF=90°,
而∠BHE+∠CBF=90°,
∴∠BHE=∠C,
∵四边形ABCD为平行四边形,
∴∠A=∠C,
∴∠A=∠BHE,所以②正确;
在△BEH和△DEC中
,
∴△BEH≌△DEC(AAS),
∴BH=CD,CE=EH,
∵点H不是DE中点
∴BE=ED≠2EC,所以①错误;
∵四边形ABCD为平行四边形,
∴AB=CD,
∴AB=BH,所以③正确;
∵∠BDH=90°+∠EBH,∠BDG=90°+∠BDE,
∵∠BDE>∠EBH,
∴∠BDG>∠BHD,
所以④错误;
故选:B.
二.填空题(共10小题)
11.若关于x的方程(a+2)x|a|﹣3x+2=0是一元二次方程,则a的值为 2 .
【分析】一元二次方程必须满足两个条件:(1)未知数的最高次数是2;(2)二次项系数不为0.
由这两个条件得到相应的关系式,再求解即可.
【解答】解:∵关于x的方程(a+2)x|a|﹣3x+2=0是一元二次方程,
∴|a|=2,a+2≠0,
解得,a=2.
故答案为:2.
12.一元二次方程x2=4的解是 x1=2,x2=﹣2 .
【分析】利用直接开平方法,将方程两边直接开平方即可.
【解答】解;x2=4,
两边直接开平方得:
x=±2,
∴x1=2,x2=﹣2,
故答案为:x1=2,x2=﹣2.
13.已知菱形ABCD中,对角线AC与BD交于点O,∠BAD=120°,AC=4,则该菱形的面积是 8 .
【分析】首先由四边形ABCD是菱形,求得AC⊥BD,OA=AC,∠BAC=∠BAD,然后在直角三角形AOB中,利用30°角所对的直角边等于斜边的一半与勾股定理即可求得OB的长,然后由菱形的面积等于其对角线积的一半,即可求得该菱形的面积.
【解答】解:∵四边形ABCD是菱形,
∴AC⊥BD,OA=OC=AC=×4=2,∠BAC=∠BAD=×120°=60°,
∴AC=4,∠AOB=90°,
∴∠ABO=30°,
∴AB=2OA=4,OB=2,
∴BD=2OB=4,
∴该菱形的面积是:AC?BD=×4×4=8.
故答案为:8.
14.Rt△ABC中,斜边AB上的高为CD,若AC=3,BC=4.则CD= .
【分析】在直角△ABC中,AB为斜边,已知AC,BC根据勾股定理即可求AB的长度,根据面积法即可求CD的长度.
【解答】解:在Rt△ABC中,AB为斜边,
AC=3,BC=4,则AB==5,
△ABC的面积S=AC?BC=AB?CD
解得CD=,
故答案为.
15.如图,E为?ABCD外一点,且EB⊥BC,ED⊥CD,若∠E=65°,则∠A的度数为 115° .
【分析】根据四边形内角和360°求出∠C度数,再借助平行四边形的性质可知∠A=∠C即可得到结果.
【解答】解:在四边形BCDE中,∠E=65°,∠EBC=∠EDC=90°,
所以∠C=360°﹣65°﹣90°﹣90°=115°.
∵四边形ABCD是平行四边形,
∴∠A=∠C=115°.
故答案为115°.
16.某种服装平均每天可以销售20件,每件盈利32元,在每件降价幅度不超过10元的情况下,若每件降价1元,则每天可多售出5件,若每天要盈利900元,每件应降价 2 元.
【分析】设每件应降价x元,根据每件服装的盈利×(原来的销售量+增加的销售量)=900,列出方程,求出x的值,再为了减少库存,计算得到降价多的数量即可得出答案.
【解答】解:设每件应降价x元,根据题意,得:
(32﹣x)(20+5x)=900
解方程得 x=2或x=26,
∵在降价幅度不超过10元的情况下,
∴x=26不合题意舍去,
所以每件服装应降价2元;
故答案为:2.
17.有一个人患了流感,经过两轮传染后得知第二次被传染的有420人,如果每轮传染率都相同,那么每轮传染中平均一个人传染了 20 个人.
【分析】设每轮传染中平均每个人传染了x人,第一轮后有(1+x)人患了流感,第二轮后会传染给x(1+x)人,然后根据第二次被传染的有420人就可以列出方程求解.
【解答】解:设每轮传染中平均每个人传染了x人.
依题意得x(1+x)=420,
∴x2+x﹣420=0,
∴(x+21)(x﹣20)=0
∴x1=20,x=﹣21(不合题意,舍去).
所以,每轮传染中平均一个人传染给20个人.
故答案为:20.
18.菱形ABCD中,∠A=60°,AB=9,点P是菱形ABCD内一点,PB=PD=3,则AP的长为 3或6 .
【分析】分成P在OA上和P在OC上两种情况进行讨论,根据△ABD是等边三角形,即可求得OA的长度,在直角△OBP中利用勾股定理求得OP的长,则AP即可求得.
【解答】解:设AC和BE相交于点O.
当P在OA上时,
∵AB=AD,∠A=60°,
∴△ABD是等边三角形,
∴BD=AB=9,OB=OD=BD=.
则AO===.
在直角△OBP中,OP===.
则AP=OA﹣OP﹣=3;
当P在OC上时,AP=OA+OP==6.
故答案是:3或6.
19.已知菱形ABCD的两条对角线分别为6和8,M、N分别是边BC、CD的中点,P是对角线BD上一点,则PM+PN的最小值= 5 .
【分析】作M关于BD的对称点Q,连接NQ,交BD于P,连接MP,此时MP+NP的值最小,连接AC,求出CP、PB,根据勾股定理求出BC长,证出MP+NP=QN=BC,即可得出答案.
【解答】解:
作M关于BD的对称点Q,连接NQ,交BD于P,连接MP,此时MP+NP的值最小,连接AC,
∵四边形ABCD是菱形,
∴AC⊥BD,∠QBP=∠MBP,
即Q在AB上,
∵MQ⊥BD,
∴AC∥MQ,
∵M为BC中点,
∴Q为AB中点,
∵N为CD中点,四边形ABCD是菱形,
∴BQ∥CD,BQ=CN,
∴四边形BQNC是平行四边形,
∴NQ=BC,
∵四边形ABCD是菱形,
∴CP=AC=3,BP=BD=4,
在Rt△BPC中,由勾股定理得:BC=5,
即NQ=5,
∴MP+NP=QP+NP=QN=5,
故答案为:5.
20.如图,在矩形ABCD中,BD为对角线,过点C作CE⊥BD,交AB于点E,点F在BC上,AF交CE于点G,且AG=GF=CF,BD=,则线段AB的长为 .
【分析】连接AC交BD于O,BD交AF于M,连接GO,CM,CE交BD于点N.利用全等三角形的性质证明OC=CM,∠ACG=∠GCM,作GK⊥CM交CM的延长线于K,作GJ⊥AC于J.则有GJ=GK,可得==,推出==,推出AG=2GM,证明△MOG≌△MBF(AAS),可得OG=BF=GM=FM,设GM=k,则GM=BF=MF=OG=k,AG=FG=CF=2k,利用勾股定理构建方程组即可解决问题.
【解答】解:连接AC交BD于O,BD交AF于M,连接GO,CM,CE交BD于点N.
∵四边形ABCD是矩形,
∴OA=OC,
∵AG=GF=CF,
∴∠FCG=∠FGC,OG∥CF,
∴∠OGC=∠FCG=∠FGC,
∵CE⊥BD,
∴∠GNO=∠GNM=90°,
∵GN=GN,
∴△GNO≌△GNM(ASA),
∴ON=NM,OG=GM,
∵∠CNO=∠CNM=90°,CN=CN,
∴△CNO≌△CNM(SAS),
∴∠OCN=∠MCN,OC=MC=AC,
∴GC平分∠ACM,作GK⊥CM交CM的延长线于K,作GJ⊥AC于J.则有GJ=GK,
∴==,
∴==,
∴AG=2GM,
∵AG=GF,
∴GM=MF,
∵∠MOG=∠MBF,∠OMG=∠BMF,
∴△MOG≌△MBF(AAS),
∴OG=BF=GM=FM,设GM=k,则GM=BF=MF=OG=k,AG=FG=CF=2k,
∴BC=3k,
在Rt△ABF中,∵AF2=AB2+BF2,
∴(4k)2=k2+AB2①,
在Rt△ABC中,∵AC2=BC2+AB2,AC=BD=,
∴()2=(3k)2+AB2②,
由①②可得AB=.
故答案为.
三.解答题(共7小题)
21.解下列方程:
(1)x2﹣6x+9=0;
(2)x2﹣4x=12;
(3)3x(2x﹣5)=4x﹣10.
【分析】(1)根据完全平方公式即可求解;
(2)根据十字相乘法即可求解;
(3)根据提公因式法即可求解.
【解答】解:(1)x2﹣6x+9=0
(x﹣3)2=0
x﹣3=0
∴x1=x2=3;
(2)x2﹣4x=12
x2﹣4x﹣12=0
(x+2)(x﹣6)=0
x+2=0或x﹣6=0
∴x1=﹣2,x2=6;
(3)3x(2x﹣5)=4x﹣10
3x(2x﹣5)﹣2(2x﹣5)=0
(2x﹣5)(3x﹣2)=0
2x﹣5=0或3x﹣2=0
∴x1=,x2=.
22.如图所示,在每个小正方形的边长均为1的网格中,线段AB的端点A、B均在小正方形的顶点上.
(1)在图中画出以AB为一边的等腰Rt△ABC,点C在小正方形的顶点上,且△ABC的面积为5;
(2)在 (1)的条件下,直接写出△ABC的周长是 2+2 .
【分析】(1)直接利用等腰三角形的性质结合三角形面积求法得出答案;
(2)直接利用勾股定理和三角形的面积公式计算即可.
【解答】解:(1)如图所示:△ABC即为所求;
(2)∵AB==2,AC=BC==,
∴△ABC的周长为:2+2,
故答案为:2+2,
23.如图,我国一渔政船航行到A处时,发现正东方向的我国领海区域B处有一可疑渔船,正在以20海里/时的速度向西北方向航行,我国渔政船立即沿北偏东60°方向航行,2小时后,在我国领海区域的C处截获可疑渔船,求渔政船的航行速度(结果保留根号).
【分析】作CD⊥AB于点D,垂足为D,首先在Rt△BCD中求得CD的长,然后在Rt△ACD中求得AC的长度,即可求出渔政船的航行速度.
【解答】解:作CD⊥AB于点D,垂足为D,
在Rt△BCD中,
∵BC=20×2=40(海里),∠CBD=45°,
∴CD=BC?sin45°=40×=20(海里),
则在Rt△ACD中,
AC==40(海里),
则渔政船的航行速度为40÷2=20海里/时.
24.如图,在△ABC中,D是BC边的中点,分别过点B、C作射线AD的垂线,垂足分别为E、F,连接BF、CE.
(1)求证:四边形BECF是平行四边形;
(2)若AF=FD,在不添加辅助线的条件下,直接写出与△ABD面积相等的所有三角形.
【分析】(1)根据全等三角形的判定和性质得出ED=FD,进而利用平行四边形的判定证明即可;
(2)利用三角形的面积解答即可.
【解答】(1)证明:在△ABF与△DEC中
∵D是BC中点,
∴BD=CD
∵BE⊥AE,CF⊥AE
∴∠BED=∠CFD=90°,
在△ABF与△DEC中
,
∴△BED≌△CFD(AAS)
∴ED=FD,
∵BD=CD
∴四边形BFEC是平行四边形;
(2)与△ABD面积相等的三角形有△ACD、△CEF、△BEF、△BEC、△BFC.
25.六一儿童节,某玩具经销商在销售中发现:某款玩具若以每个50元销售,一个月能售出500个,销售单价每涨1元,月销售量就减少10个,这款玩具的进价为每个40元,请回答以下问题:
(1)若月销售利润定为8000元,且尽可能让利消费者,销售单价应定为多少元?
(2)由于资金问题,在月销售成本不超过10000元、且没有库存积压的情况下,问销售单价至少定为多少元?
【分析】(1)根据“销售单价每涨1元,月销售量就减少10件”,可知:月销售量=500﹣(销售单价﹣50)×10,然后根据月销售利润=每件的利润×销售的数量列出方程并解答;
(2)设销售单价定为a元,根据“在月销售成本不超过10000元”列出不等式,并解答.
【解答】解:(1)设销售单价应定为x元,
由题意,得(x﹣40)[500﹣10(x﹣50)]=8000,
解得x1=60,x2=80,
∵尽可能让利消费者,
∴x=60.
答:消费单价应定为60元.
(2)设销售单价定为a元,
由题意,得40[500﹣10(a﹣50)]≤10000,
解得a≥75
答:销售单价至少定为75元.
26.已知正方形ABCD,M是直线BC上的一点,过点B作BE⊥DM于点E,交直线CD于点F,过点F作FG∥BC交直线BD于点G.
(1)如图1,点M在线段BC上时,直接写出FG、MC、AD之间的数量关系 FG=MC+AD ;
(2)如图2,点M在线段BC的延长线上时,求证:FG+MC=BC;
(3)如图3,过点E作EN⊥BD于点N,连接AN,若S△EFD=DF2,AB=4,求AN的长.
【分析】(1)结论:FG=MC+AD.证明△BCF≌△DCM(AAS)即可解决问题.
(2)证明△BCF≌△DCM(AAS),利用全等三角形的性质即可解决问题.
(3)如图3中,作AR⊥BD于R,EH⊥CD于H,取DF的中点T,连接TE.首先证明∠CDM=15°,推出∠DBE=30°即可解决问题.
【解答】(1)解:结论:FG=MC+AD.
理由:如图1中,
∵四边形ABCD是正方形,
∴∠DBC=∠BDC=45°,BC=CD,∠BCD=90°,
∵BE⊥DM,
∴∠BEM=90°,
∴∠EBM+∠BME=90°,∠EBM+∠BFC=90°,
∴∠BME=∠BFC.又∵∠BCF=∠DCM=90°,BC=CD,
∴△BCF≌△DCM(AAS),
∴FC=CM.
又∵GF∥BC,
∴∠DGF=∠DBC=45°=∠BDC,
∴GF=DF,
∴FG=CD+CF=AD+CM.
故答案为:FG=MC+AD.
(2)证明:如图2中,
∵四边形ABCD是正方形,
∴∠DBC=∠BDC=45°,BC=CD,∠BCD=90°,
∵BE⊥DM,
∴∠BEM=90°,
∴∠EBM+∠M=90°,∠EBM+∠BFC=90°,
∴∠M=∠BFC.又∵∠BCF=∠DCM=90°,BC=CD,
∴△BCF≌△DCM(AAS),
∴FC=CM.
又∵GF∥BC,
∴∠DGF=∠DBC=45°=∠BDC,
∴GF=DF,
∴FG+MC=DF+CF=CD=BC.
(3)如图3中,作AR⊥BD于R,EH⊥CD于H,取DF的中点T,连接TE.
∵S△DEF=?DF?EH=DF2,
∴EH=DF,即DF=4EH,
∵∠DEF=90°,DT=TF,
∴TE=DF=DT=TF,
∴TE=2EH,
∴∠ETH=30°,
∵TD=TE,
∴∠TDE=∠TED,
∵∠ETH=∠TDE+∠TED,
∴∠EDT=15°,
∵△BCF≌△DCM,
∴∠CBF=∠CDM=15°,
∵∠DBC=45°,
∴∠EBN=30°,
∵BE⊥DM,
∴BE=BD?cos30°=8×=4,BN=BE?cos30°=6,
∵AR⊥BD,AB=4,∠ABR=45°,
∴AR=BR=4,
∴NR=2,
∴AN===2.
27.如图,在平面直角坐标系中,点O为坐标原点,B(2,0),点A在y轴正半轴上,AB=2.
(1)直接写出A点坐标 (0,4) ;
(2)将△AOB沿x轴正方向平移,得到△DEC,点A对应点D,点B对应点C,点O对应点E.连接AD,作∠BAD的平分线,交射线DC于点F,设E点的横坐标为t,线段CF的长为d,求d与t的关系式(不要求写出t的取值范围);
(3)在 (2)的条件下,当点F在线段DC上时,AF与DE交于点G,连接EF,若∠DFE﹣∠BAF=45°,求此时t的值,并判断坐标平面内是否存在一点M,使以点A、D、G、M为顶点的四边形是平行四边形?若存在,请求出点M的坐标;若不存在,请说明理由.
【分析】(1)在Rt△AOB中,解直角三角形求出OA即可解决问题;
(2)首先证明AD=DF=t,分两种情形:①当点F在线段CD上时,CF=CD﹣DF;当点F在CD的延长线上时,CF=DF﹣CD;
(3)首先证明当四边形ADEO是正方形时,满足条件:∠DFE﹣∠BAF=45°,求出直线AF的解析式,可得点G坐标,再利用平行四边形的性质即可解决问题.
【解答】解:(1)∵B(2,0),
∴OB=2,
在Rt△ABO中,∵∠AOB=90°,AB=2,OB=2,
∴OA===4,
∴A(0,4),
故答案为(0,4).
(2)如图1中,
由题意E(t,0).
∵OA∥DE,OA=DE,
∴四边形AOED是平行四边形,
∵∠AOE=90°,
∴四边形AOED是矩形,
∴AD=OE=t,
∵AF平分∠DAB,
∴∠DAF=∠BAF,
∵AB∥DF,
∴∠BAF=∠AFD,
∴∠DAF=∠DFA,
∴DA=DF=t,
∵AB=CD=2,
∴当点F在线段CD上时,CF=CD﹣DF=2﹣t,
当点F在CD的延长线上时,CF=DF﹣CD=t﹣2.
(3)如图,
当四边形OADE是正方形时,由(2)可知:DA=DE=DF,
∴A,E,F在以D为圆心,DA为半径的圆上,
∴∠AFE=∠ADE=45°,
∴∠DFE﹣∠BAF=∠DFE﹣∠AFD=∠AFE=45°,
∴当四边形ADEO是正方形时,满足条件:∠DFE﹣∠BAF=45°,
此时OE=OA=4,
∴t=4,E(4,0),
设直线AF交x轴于K.
∵AD∥BK,AK平分∠DAB,
∴∠BAK=∠DAK=∠AKB,
∴AB=BK=2,
∴OK=2+2,
∴直线AK的解析式为y=x+4,
∴G(4,2+2),
∵以点A,D,G,M为顶点的四边形是平行四边形,
∴M1(0,2+2),M2(8,6﹣2),M3(0,6﹣2).
同课章节目录
