沪教版高中物理选修3-5 1.4美妙的守恒定律_学案2
文档属性
| 名称 | 沪教版高中物理选修3-5 1.4美妙的守恒定律_学案2 | 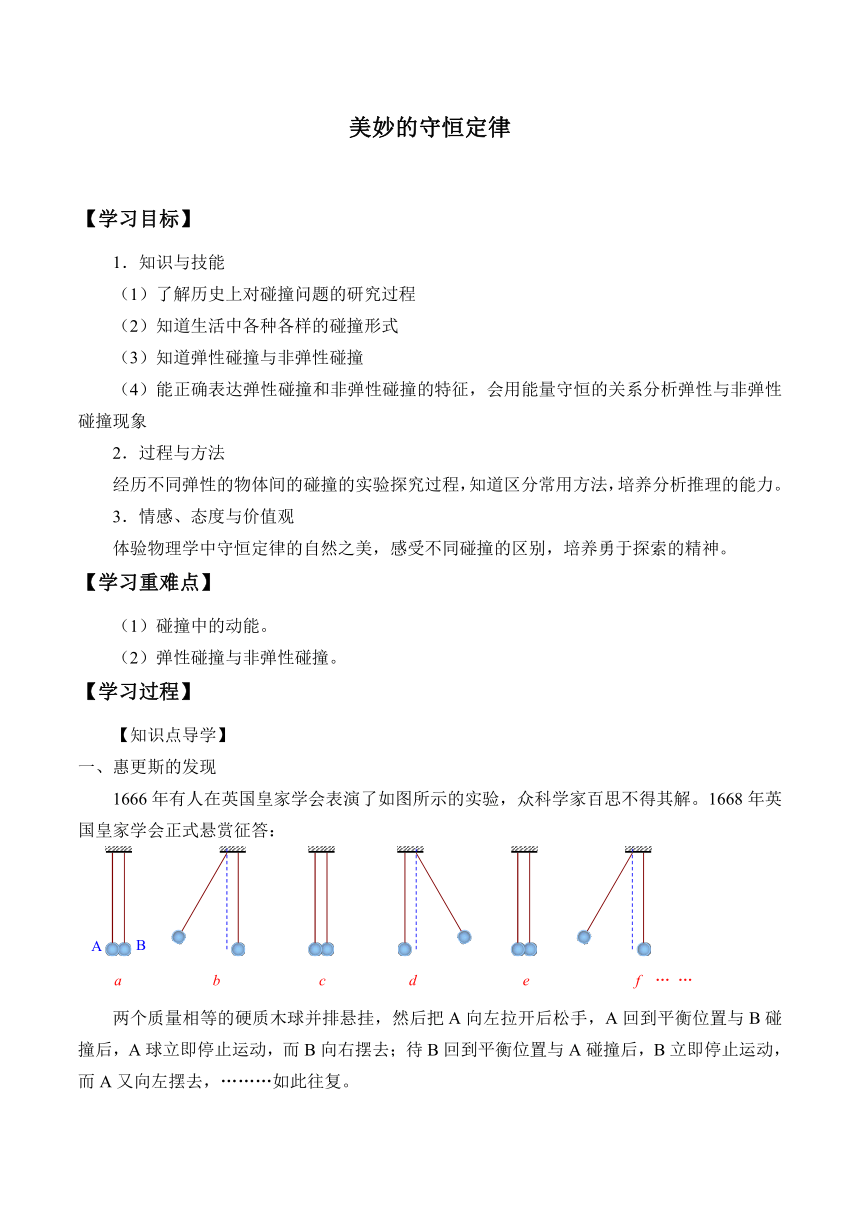 | |
| 格式 | zip | ||
| 文件大小 | 81.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-03-20 07:33:44 | ||
图片预览



文档简介
美妙的守恒定律
【学习目标】
1.知识与技能
(1)了解历史上对碰撞问题的研究过程
(2)知道生活中各种各样的碰撞形式
(3)知道弹性碰撞与非弹性碰撞
(4)能正确表达弹性碰撞和非弹性碰撞的特征,会用能量守恒的关系分析弹性与非弹性碰撞现象
2.过程与方法
经历不同弹性的物体间的碰撞的实验探究过程,知道区分常用方法,培养分析推理的能力。
3.情感、态度与价值观
体验物理学中守恒定律的自然之美,感受不同碰撞的区别,培养勇于探索的精神。
【学习重难点】
(1)碰撞中的动能。
(2)弹性碰撞与非弹性碰撞。
【学习过程】
【知识点导学】
一、惠更斯的发现
1666年有人在英国皇家学会表演了如图所示的实验,众科学家百思不得其解。1668年英国皇家学会正式悬赏征答:
两个质量相等的硬质木球并排悬挂,然后把A向左拉开后松手,A回到平衡位置与B碰撞后,A球立即停止运动,而B向右摆去;待B回到平衡位置与A碰撞后,B立即停止运动,而A又向左摆去,………如此往复。
荷兰物理学家惠更斯做出比较完整的分析和解释。他发现:两小球在碰撞过程中,除了动量守恒外,还有一个物理量也是守恒的——这个物理量就是动能。
请同学们记住这个有趣的实验。
二、碰撞中的动能
1.实验探究:
分析在气垫导轨上做的两组实验数据,探究碰撞前后系统的动能。发现在两滑块碰后粘在一起的实验中,系统的动能减少了;在两滑块碰后分开的实验中,系统的动能碰撞前后几乎相等。
可见在碰撞过程中,系统的动量总是守恒的,而动能可能守恒,也可能不守恒。
2.依据碰撞前后动能变化情况对碰撞进行分类:
弹性碰撞:物理学中把动量动能都守恒的碰撞,叫做弹性碰撞。
非弹性碰撞:把动能不守恒的碰撞,叫做非弹性碰撞。
后来人们弄清楚了非弹性碰撞的实质是在碰撞过程中动能损失了,转化为其他形式的能了。而弹性碰撞就是在碰撞过程中动能没有损失。真正的弹性碰撞只有在分子、原子及更小的微观粒子之间才会发生。在宏观领域,往往我们把动能损失很小的碰撞也按弹性碰撞来处理,如硬质木球之间、钢球之间等碰撞。
完全非弹性碰撞:这是一种特殊的非弹性碰撞,两物体碰后“合”为一体,以共同的速度运动。这种碰撞动能损失最多。
三、研究弹性碰撞
重点理解模型:
质量分别为m1.m2的A.B两钢球置于花水平面上,A球速度为v1,B球速度为v2,设两球发生弹性碰撞,那么碰撞后A.B的速度v1.v2是怎样的呢?
分析解决:
动能守恒
动量守恒
联解以上两式得
情况讨论:1.若m1m2,则v1′ 与v1同向
2.若m1
▼各种情况中,v2′ 与v1总是同向的
四、自然之美——物理学中的守恒定律
1.简洁美:用极简练的语言将内涵丰富的自然规律表述出来,表现出物理学的简洁美。
2.对称美:每一条守恒定律都对应于自然界中的一种对称关系,反映出自然界的一种对称美。
3.和谐统一美:每一条守恒定律都有一个守恒量,这反映了各种运动形式之间的联系与统一,表现出物理学的和谐统一美。
在物理学的应用中,在对许多新事物的预言及新理论的建立中,无不闪耀着守恒思想的光辉。在中学物理中,我们学过的守恒定律有:
机械能守恒定律
动量守恒定律
电荷守恒定律
质量守恒定律
能量守恒定律
【典例引路】
【例题】如图所示,在水平光滑直导轨上,静止着三个质量均为m=1 kg的相同小球A.B.C,现让A球以v0=2 m/s的速度向着B球运动,A.B两球碰撞后粘合在一起,两球继续向右运动并跟C球碰撞,C球的最终速度vC=1 m/s。求:
(1)A.B两球跟C球相碰前的共同速度多大?
(2)两次碰撞过程中一共损失了多少动能?
【解析】
(1)A.B相碰满足动量守恒 mv0=2mv1
得两球跟C球相碰前的速度 v1=1 m/s。
(2)两球与C碰撞同样满足动量守恒 2mv1=mvC+2mv2
得两球碰后的速度v2=0.5 m/s,
两次碰撞损失的动能
|ΔEk|=mv-×2mv-mv=1.25 J。
答案:(1)1 m/s (2)1.25 J
【达标检测】
1.如图所示与轻弹簧相连的物体A停放在光滑的水平面上。物体B沿水平方向向右运动,跟与A相连的轻弹簧相碰。在B跟弹簧相碰后,对于A.B和轻弹簧组成的系统,下列说法中正确的是( )
A.弹簧压缩量最大时,A.B的速度相同
B.弹簧压缩量最大时,A.B的动能之和最小
C.弹簧被压缩的过程中系统的总动量不断减小
D.物体A的速度最大时,弹簧的弹性势能为零
2.如图所示,一轻弹簧左端固定在长木板M的左端,右端与小木块m连接,且m、M及M与地面间接触光滑。开始时,m和M均静止,现同时对m、M施加等大反向的水平恒力F1和F2,从两物体开始运动以后的整个运动过程中,弹簧形变不超过其弹性限度,对于m、M和弹簧组成的系统( )
A.由于F1.F2等大反向,故系统机械能守恒
B.当弹簧弹力大小与F1.F2大小相等时,m、M各自的动能最大
C.由于F1.F2大小不变,所以m、M各自一直做匀加速运动
D.由于F1.F2等大反向,故系统的动量始终为零?
3.如图所示,小车在光滑水平面上向左匀速运动,轻质弹簧左端固定在A点,物体用线拉在A点将弹簧压缩,某时刻线断了,物体沿车滑动到B端粘在B端的油泥上,则下述说法中正确的是( )
①若物体滑动中不受摩擦力,则全过程机械能守恒
②若物体滑动中有摩擦力,则全过程动量守恒
③两种情况下,小车的最终速度与断线前相同
④两种情况下,系统损失的机械能相同
A.①②③ B.②③④ C.①③④ D.①②③④
4.在光滑水平地面上有两个相同的弹性小球A.B,质量都为m。现B球静止,A球向B球运动,发生正碰。已知碰撞过程中总机械能守恒,且两球压缩到距离最小时的系统的弹性势能为Ep,则碰前A球的速度等于( )
A. B. C.2 D.2
5.在光滑水平面上,动能为E0、动量的大小为p0的小钢球1与静止小钢球2发生碰撞,碰撞前后球1的运动方向相反。将碰撞后球1的动能和动量的大小分别记为E1.p1,球2的动能和动量的大小分别记为E2.p2,则下列说法中不正确的是( )
A.E1<E0 B.p1<p0 C.E2>E0 D.p2>p0
6.甲、乙两个小孩各乘一辆冰车在水平冰面上游戏,如图所示。甲和她的冰车质量共为30 kg,乙和他的冰车质量也是30 kg。游戏时,甲推着一个质量为15 kg的箱子,共同以2 m/s的速度滑行。乙以同样大小的速率迎面滑来。为避免相撞,甲突然将箱子沿冰面推给乙。箱子滑到乙处时乙迅速把它抓住。若不计摩擦。甲要以如下哪个速度(相对于冰面)将箱子推出,才能避免与乙相撞?( )
①4 m/s ②5 m/s ③6 m/s ④7 m/s
A.①②③④都可以 B.②③④都可以 C.③④都可以 D.只有④可以?
7.如图所示,A.B两小球在光滑水平面上分别以动量p1=4 kg·m/s和p2=6 kg·m/s(向右为参考正方向)做匀速直线运动,则在A球追上B球并与之碰撞的过程中,两小球的动量变化量Δp1和Δp2可能分别为( )
A.-2 kg·m/s,3 kg·m/s B.-8 kg·m/s,8 kg·m/s
C.1 kg·m/s,-1 kg·m/s D.-2 kg·m/s,2 kg·m/s
8.如图,在光滑水平地面上有三个完全相同的小球排成一条直线。2.3小球静止,并靠拢在一起,1球以速度v0射向它们,设碰撞中不损失机械能,则碰后三个小球的速度可能值是( )
A.v1=v2=v3=v0/3 B.v1=0,v2=v3=v0/2
C.v1=v0/2,v2=v3=0 D.v1=v2=0,v3=v0
9.(2009·山东高考)如图。所示,光滑水平直轨道上有三个滑块A.B.C,质量分别为mA=mC=2m,mB=m,A.B用细绳连接,中间有一压缩的轻弹簧(弹簧与滑块不拴接)。开始时A.B以共同速度v0运动,C静止。某时刻细绳突然断开,A.B被弹开,然后B又与C发生碰撞并粘在一起,最终三滑块速度恰好相同。求B与C碰撞前B的速度。
10.如图所示,两个质量均为m的物块A.B通过轻弹簧连在一起静止于光滑水平面上。另一物块C以一定的初速度向右匀速运动,与A发生碰撞并粘在一起。若要使弹簧具有最大弹性势能时,A.B.C及弹簧组成的系统的动能刚好是势能的2倍,则C的质量应满足什么条件?
【参考答案】
1.ABD 2.BD 3.B 4.C 5.C 6.C
7.【解析】 考虑到碰撞过程动量必须是守恒的,对于选项A,有
Δp1+Δp2=-2 kg·m/s+3 kg·m/s=1 kg·m/s≠0?
可以判断A选项是错误的。
考虑到碰撞过程中,两球的动能不可能增加,对选项B,碰撞前两球的总动能为
Ek=?
碰后两球的总动能为
Ek′=
由于Ek′>Ek,可以判断B选项是错误的。从动力学的角度出发考虑,碰撞过程中A.B所受的力应分别向左和向右,这样应有:Δp1<0 Δp2>0显然C选项是错误的。
8.D
9.解析:
设共同速度为v,滑块A与B分开后,B的速度为vB,
由动量守恒定律:(mA+mB)v0=mAv+mBvB ①
mBvB=(mB+mC)v ②
联立①②式,得B与C碰撞前B的速度为
vB=v0. 答案:v0
10.解析:
A与C发生碰撞的过程中动量守恒,有:
mCv0=(mC+m)v1
当弹簧弹性势能最大时,A.B.C速度相等,由动量守恒得:
(mC+m)v1=(mC+2m)v2
A和C粘合后至A.B.C达到共同速度的过程中,A.B.C组成的系统机械能守恒,
所以有:
(m+mC)v=(mC+2m)v+Ep
Ep=(mC+2m)v
联立上述各式得mC=m。
答案:mC=m
a b c d e f … …
A
B
A v1 B
v′1 v′2
v
B
A
vt
同课章节目录
