人教版八年级数学下册 18.1.1平行四边形的性质 说课教案
文档属性
| 名称 | 人教版八年级数学下册 18.1.1平行四边形的性质 说课教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 117.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-20 09:24:35 | ||
图片预览


文档简介
《平行四边形的性质》说课稿
各位老师:
大家好!
今天我模课的题目是《平行四边形的性质》。
一、教学目标
知识与技能目标:理解平行四边形的定义,探究平行四边形的性质;利用平行四边形的性质进行有关的证明和计算,解决简单的实际问题;
过程与方法目标:通过观察、猜测、归纳、证明,能运用数学语言合乎逻辑地进行讨论与质疑,发展学生合理的推理意识,培养主动探究的习惯;
情感态度与价值观目标:通过平行四边形性质的应用过程,培养学生独立思考的习惯,进一步认识数学与生活的密切联系,体验数学来源于生活又服务于生活。
?
二、教学重点、难点
(1)重点:平行四边形性质的探究与应用。
(2)难点:添加辅助线将平行四边形问题转化为三角形问题。
?三、教学过程
(一)温故思新,情境导入
首先复习四边形的定义及四边形的有关性质然后课件显示章前图和一些图片提出问题:你能从图中找出我们熟悉的几何图形吗?
(二)自主学习,发现问题
通过观察图片,让学生举出身边存在的平行四边形的例子,为学生提供参与活动的时间和空间。
然后给出一些图片,教师出示问题:
通过观察图片,找出图形的共同特征,说出平行四边形的定义?
有两组对边分别平行的四边形叫做平行四边形
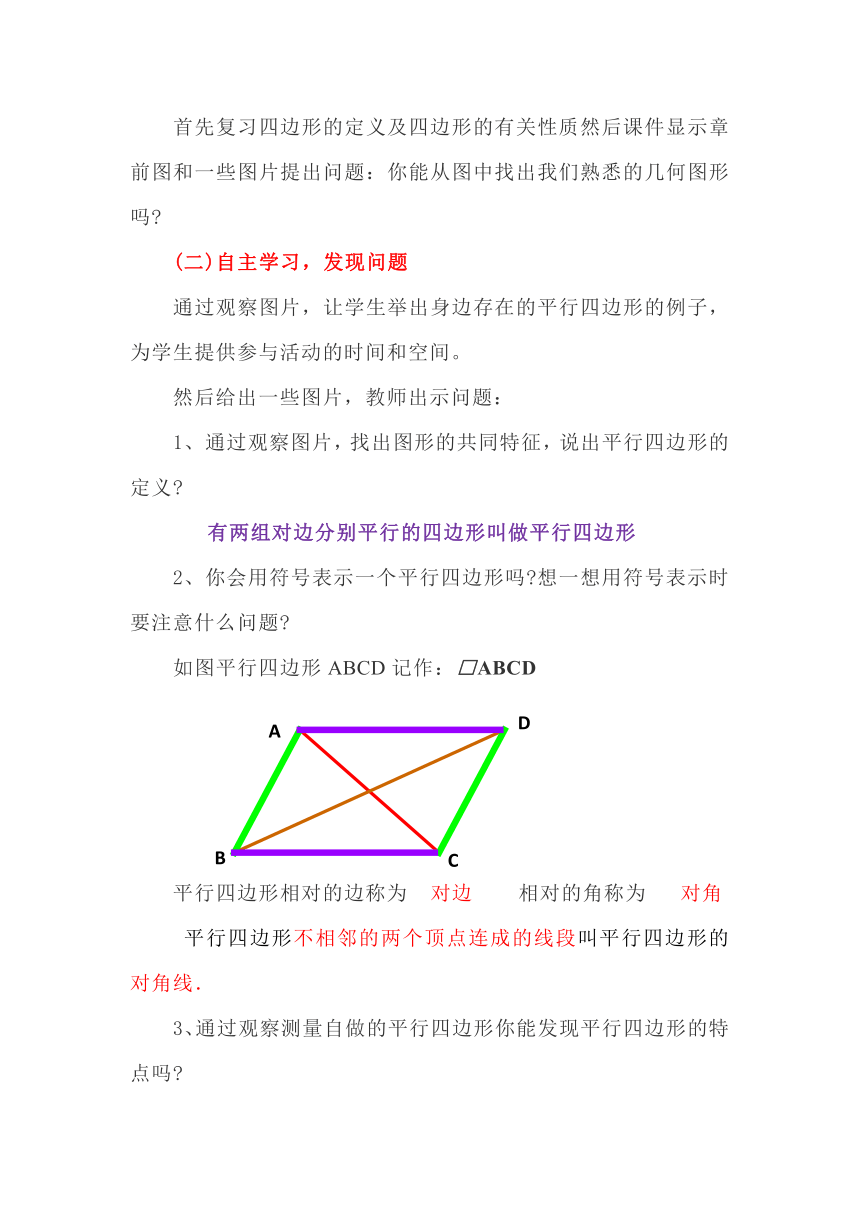
2、你会用符号表示一个平行四边形吗?想一想用符号表示时要注意什么问题?
如图平行四边形ABCD记作:□ABCD
平行四边形相对的边称为 对边 相对的角称为 对角
平行四边形不相邻的两个顶点连成的线段叫平行四边形的对角线.
3、通过观察测量自做的平行四边形你能发现平行四边形的特点吗?
边:对边平行且相等
角:对角相等,邻角互补
4、你能证明你发现的结论吗?
教师巡视引导,帮助学生自学。?
(三)合作交流,解决问题
小组合作交流,共同解决学习过程中发现的问题:寻找证明的方法。
当学生有疑惑时,教师巡视辅导:我们目前证明线段、角相等的方法是什么?(利用三角形全等来证明)而图中没有三角形该怎么办?(引导学生得出需构造辅助线,将四边形问题转化为三角形问题来解决学生完成证明。)
归纳平行四边形的性质:平行四边形的对边相等;平行四边形的对角相等,邻角互补,平行四边形是中心对称图形。并引导学生写出性质的几何语言。?
(四)小组展示,学以致用
1、小组代表展示交流的结果,通过PPT讲解平行四边形性质,培养学生语言组织能力和逻辑思维能力。
2、探究例1:
在□ABCD中,已知∠A=52° ,求其余三个角的度数。
引导学生审题,学生弄清题意后教师示范解题过程,并重点强调解答中平行四边形性质的几何表述。
课堂练习,巩固新知
(1)平行四边形的一组对角度数之和为200°,则平行四边形中较大的角为 。
(2)在□ABCD中,AD=3,BD⊥AD, 且BD=4, 你能求出平行四边形的周长吗?(先引导学生解题,再示范解题过程)
四、课堂小结:
1、这节课你的收获是什么?
2、还有什么困惑?
五、作业设计,强化新知
1、选择题:
(1)平行四边形的两邻角的角平分线相交所成的角为( )
A、锐角 B、直角 C、钝角 D、不能确定
(2)平行四边形的周长为24cm,相邻两边的差为2cm,则平行四边形的各边长为(? )
A、4cm,4cm,8cm,8cm B、5cm,5cm,7cm,7cm
C、5.5cm,5.5cm,6.5cm,6.5cm D、3cm,3cm,9cm,9cm
(3)下面的性质中,平行四边形不一定具有的是( )
A、对角互补 B、邻角互补 C、对角相等 D、对边相等
2、填空题:
(1)如图所示,DE∥AB,EF∥BC,DF∥AC,图中有 个平行四边形。
3、解答题:
如图,小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m,其他三条边各长多少?
?
六 、板书设计
平行四边形的性质
定义:两组对边分别平行的四边形叫平行四边形。???????
?例1:(略)
记作:□ABCD
性质: 平行四边形的对边相等且平行;
平行四边形的对角相等,邻角互补
平行四边形的对角线互相平分
平行四边形是中心对称图形。
A
D
B
C
A
B
C
D
52°
D
A
A
B
C
D
B
C
各位老师:
大家好!
今天我模课的题目是《平行四边形的性质》。
一、教学目标
知识与技能目标:理解平行四边形的定义,探究平行四边形的性质;利用平行四边形的性质进行有关的证明和计算,解决简单的实际问题;
过程与方法目标:通过观察、猜测、归纳、证明,能运用数学语言合乎逻辑地进行讨论与质疑,发展学生合理的推理意识,培养主动探究的习惯;
情感态度与价值观目标:通过平行四边形性质的应用过程,培养学生独立思考的习惯,进一步认识数学与生活的密切联系,体验数学来源于生活又服务于生活。
?
二、教学重点、难点
(1)重点:平行四边形性质的探究与应用。
(2)难点:添加辅助线将平行四边形问题转化为三角形问题。
?三、教学过程
(一)温故思新,情境导入
首先复习四边形的定义及四边形的有关性质然后课件显示章前图和一些图片提出问题:你能从图中找出我们熟悉的几何图形吗?
(二)自主学习,发现问题
通过观察图片,让学生举出身边存在的平行四边形的例子,为学生提供参与活动的时间和空间。
然后给出一些图片,教师出示问题:
通过观察图片,找出图形的共同特征,说出平行四边形的定义?
有两组对边分别平行的四边形叫做平行四边形
2、你会用符号表示一个平行四边形吗?想一想用符号表示时要注意什么问题?
如图平行四边形ABCD记作:□ABCD
平行四边形相对的边称为 对边 相对的角称为 对角
平行四边形不相邻的两个顶点连成的线段叫平行四边形的对角线.
3、通过观察测量自做的平行四边形你能发现平行四边形的特点吗?
边:对边平行且相等
角:对角相等,邻角互补
4、你能证明你发现的结论吗?
教师巡视引导,帮助学生自学。?
(三)合作交流,解决问题
小组合作交流,共同解决学习过程中发现的问题:寻找证明的方法。
当学生有疑惑时,教师巡视辅导:我们目前证明线段、角相等的方法是什么?(利用三角形全等来证明)而图中没有三角形该怎么办?(引导学生得出需构造辅助线,将四边形问题转化为三角形问题来解决学生完成证明。)
归纳平行四边形的性质:平行四边形的对边相等;平行四边形的对角相等,邻角互补,平行四边形是中心对称图形。并引导学生写出性质的几何语言。?
(四)小组展示,学以致用
1、小组代表展示交流的结果,通过PPT讲解平行四边形性质,培养学生语言组织能力和逻辑思维能力。
2、探究例1:
在□ABCD中,已知∠A=52° ,求其余三个角的度数。
引导学生审题,学生弄清题意后教师示范解题过程,并重点强调解答中平行四边形性质的几何表述。
课堂练习,巩固新知
(1)平行四边形的一组对角度数之和为200°,则平行四边形中较大的角为 。
(2)在□ABCD中,AD=3,BD⊥AD, 且BD=4, 你能求出平行四边形的周长吗?(先引导学生解题,再示范解题过程)
四、课堂小结:
1、这节课你的收获是什么?
2、还有什么困惑?
五、作业设计,强化新知
1、选择题:
(1)平行四边形的两邻角的角平分线相交所成的角为( )
A、锐角 B、直角 C、钝角 D、不能确定
(2)平行四边形的周长为24cm,相邻两边的差为2cm,则平行四边形的各边长为(? )
A、4cm,4cm,8cm,8cm B、5cm,5cm,7cm,7cm
C、5.5cm,5.5cm,6.5cm,6.5cm D、3cm,3cm,9cm,9cm
(3)下面的性质中,平行四边形不一定具有的是( )
A、对角互补 B、邻角互补 C、对角相等 D、对边相等
2、填空题:
(1)如图所示,DE∥AB,EF∥BC,DF∥AC,图中有 个平行四边形。
3、解答题:
如图,小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m,其他三条边各长多少?
?
六 、板书设计
平行四边形的性质
定义:两组对边分别平行的四边形叫平行四边形。???????
?例1:(略)
记作:□ABCD
性质: 平行四边形的对边相等且平行;
平行四边形的对角相等,邻角互补
平行四边形的对角线互相平分
平行四边形是中心对称图形。
A
D
B
C
A
B
C
D
52°
D
A
A
B
C
D
B
C
