人教版八年级下册数学17.1.1:勾股定理 课件(共26张PPT)
文档属性
| 名称 | 人教版八年级下册数学17.1.1:勾股定理 课件(共26张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-20 00:00:00 | ||
图片预览



文档简介
(共26张PPT)
八年级数学(上册)?人教版
探索勾股定理
黄堡镇中心学校八年级数学组
你见过这个漂亮的图案吗?
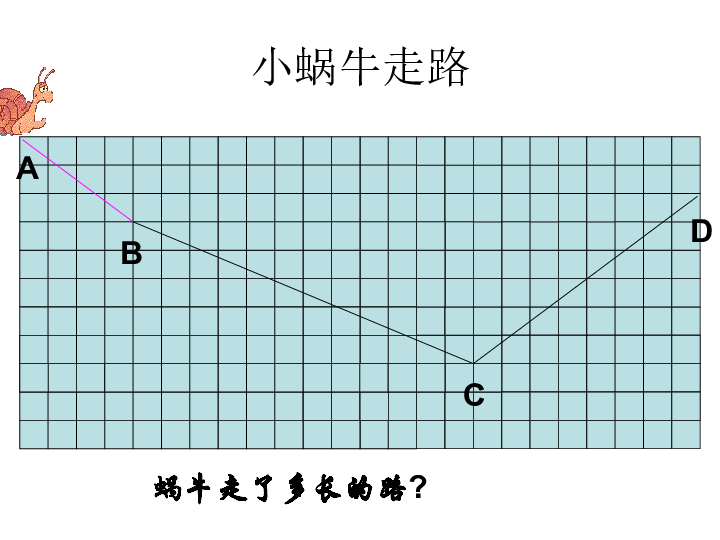
小蜗牛走路
A
B
C
D
蜗牛走了多长的路?
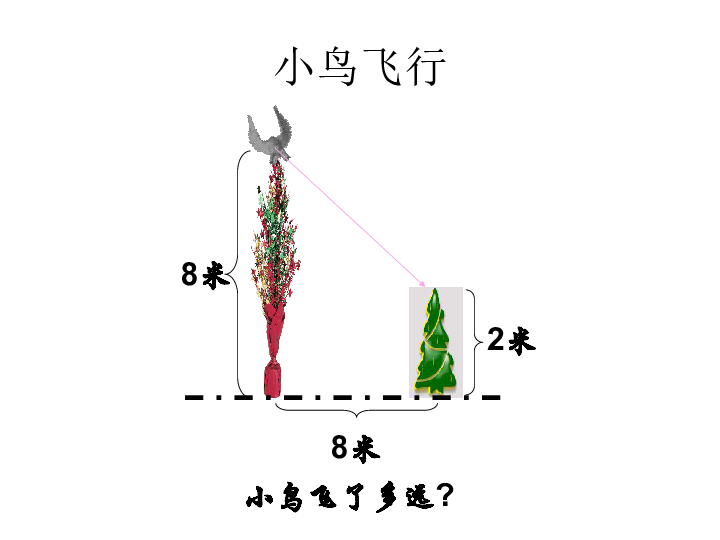
小鸟飞行
小鸟飞了多远?
8米
飞机的速度有
多少啊???
北
南
西
东
港口
A
B
轮 船 航 海
返回
相传2500年前,毕达哥拉斯有一次在朋友家里做客时,发现朋友家用砖铺成的地面中反映了直角三角形三边的某种数量关系.
我们也来观察右图中的地面,看看有什么发现?
数学家毕达哥拉斯的发现:
A、B、C的面积有关系
由此能否得到直角三角形三边有关系?
SA+SB=SC
两直边的平方和等于斜边的平方
研讨:如图所示,每个小方格代表一个单位面积。
观察图(1):正方形A、B、C的面积各是多少?
观察图(2):正方形A、B、C的面积各是多少?
你能得到什么推断?
根据图形所示填表:
A的面积 B的面积 C的面积
图(3)
图(4)
a
c
b
?
?
下面我们介绍——赵爽证法
请先用手中的全等直角三角形按图示进行摆放,然后根据图示的边长,选择其中一个图形,分析其面积关系后证明.
图1
图2
图3
自主证明
图1
图3
解:
解:
(2)使用前提是直角三角形
(3)分清直角边、斜边
返回
勾股定理的简单应用
1、如图中的各个直角三角形,求未知边的长。
勾股定理的应用一:蜗牛走路
小蜗牛从A点沿图中的折线ABCD到D点,如果
每个小方格的边长是一分米,那么它走了多少米?
A
B
C
D
解:由图可知
所以蜗牛走的路为5+13+10=28分米, 即2.8米
勾股定理的应用二:小鸟飞行
如图.有两棵数,一棵高8米,另一棵高2米,两树相距
8米,一只小鸟从一棵数的梢飞到另一棵树的树梢
求小鸟至少飞了多少米?
8米
勾股定理的应用二:小鸟飞行
如图.有两棵数,一棵高8米,另一棵高2米,两树相距
8米,一只小鸟从一棵数的梢飞到另一棵树的树梢
求小鸟至少飞了多少米?
则CE=AD=8m,BE=AB-CD=6m
答:至少飞行10米
D
勾股定理的应用三:生活实例
3、飞机在空中水平飞行某一时刻刚好飞到一男孩
头顶正上方4000米处,过了20秒,飞机距离这个男孩
头顶5000米,求飞机速度?
分析:求BC
勾股定理的应用三:生活实例
3、飞机在空中水平飞行某一时刻刚好飞到一男孩
头顶正上方4000米处,过了20秒,飞机距离这个男孩
头顶5000米,求飞机飞行了多少千米?
勾股定理的应用四:航海问题
甲轮船以15海里/时的速度从港口向东北方向航
行,乙船同时以20海里/时速度向东南方向航行
求它们离开港口2小时后相距多远?
北
南
西
东
港口
分析:求AB
A
B
勾股定理的应用四:航海问题
甲轮船以15海里/时的速度从港口向东南方向航
行,乙船同时以20海里/时速度向东北方向航行
求它们离开港口2小时后相距多远?
北
南
西
东
港口
A
B
返回
⒈ 勾股定理是几何中最重要的定理之一,它揭示了直
角三角形三边之间的数量关系.
⒊勾股定理的主要作用是:
在直角三角形中,已知任意两边求第三边的长.
巩固练习
1、如图,在高为3米,斜坡长为5米的楼梯表面铺
地毯,则地毯长度至少需 米.
2、在三角形ABC中, C=90 AC=4,BC=3
求斜边AB边上的高CD。
3、如图:已知AD=14, AB=6, DC=8, BE=EC=y
求AE,ED及y的长。
A
E
D
C
B
6
8
y
y
八年级数学(上册)?人教版
探索勾股定理
黄堡镇中心学校八年级数学组
你见过这个漂亮的图案吗?
小蜗牛走路
A
B
C
D
蜗牛走了多长的路?
小鸟飞行
小鸟飞了多远?
8米
飞机的速度有
多少啊???
北
南
西
东
港口
A
B
轮 船 航 海
返回
相传2500年前,毕达哥拉斯有一次在朋友家里做客时,发现朋友家用砖铺成的地面中反映了直角三角形三边的某种数量关系.
我们也来观察右图中的地面,看看有什么发现?
数学家毕达哥拉斯的发现:
A、B、C的面积有关系
由此能否得到直角三角形三边有关系?
SA+SB=SC
两直边的平方和等于斜边的平方
研讨:如图所示,每个小方格代表一个单位面积。
观察图(1):正方形A、B、C的面积各是多少?
观察图(2):正方形A、B、C的面积各是多少?
你能得到什么推断?
根据图形所示填表:
A的面积 B的面积 C的面积
图(3)
图(4)
a
c
b
?
?
下面我们介绍——赵爽证法
请先用手中的全等直角三角形按图示进行摆放,然后根据图示的边长,选择其中一个图形,分析其面积关系后证明.
图1
图2
图3
自主证明
图1
图3
解:
解:
(2)使用前提是直角三角形
(3)分清直角边、斜边
返回
勾股定理的简单应用
1、如图中的各个直角三角形,求未知边的长。
勾股定理的应用一:蜗牛走路
小蜗牛从A点沿图中的折线ABCD到D点,如果
每个小方格的边长是一分米,那么它走了多少米?
A
B
C
D
解:由图可知
所以蜗牛走的路为5+13+10=28分米, 即2.8米
勾股定理的应用二:小鸟飞行
如图.有两棵数,一棵高8米,另一棵高2米,两树相距
8米,一只小鸟从一棵数的梢飞到另一棵树的树梢
求小鸟至少飞了多少米?
8米
勾股定理的应用二:小鸟飞行
如图.有两棵数,一棵高8米,另一棵高2米,两树相距
8米,一只小鸟从一棵数的梢飞到另一棵树的树梢
求小鸟至少飞了多少米?
则CE=AD=8m,BE=AB-CD=6m
答:至少飞行10米
D
勾股定理的应用三:生活实例
3、飞机在空中水平飞行某一时刻刚好飞到一男孩
头顶正上方4000米处,过了20秒,飞机距离这个男孩
头顶5000米,求飞机速度?
分析:求BC
勾股定理的应用三:生活实例
3、飞机在空中水平飞行某一时刻刚好飞到一男孩
头顶正上方4000米处,过了20秒,飞机距离这个男孩
头顶5000米,求飞机飞行了多少千米?
勾股定理的应用四:航海问题
甲轮船以15海里/时的速度从港口向东北方向航
行,乙船同时以20海里/时速度向东南方向航行
求它们离开港口2小时后相距多远?
北
南
西
东
港口
分析:求AB
A
B
勾股定理的应用四:航海问题
甲轮船以15海里/时的速度从港口向东南方向航
行,乙船同时以20海里/时速度向东北方向航行
求它们离开港口2小时后相距多远?
北
南
西
东
港口
A
B
返回
⒈ 勾股定理是几何中最重要的定理之一,它揭示了直
角三角形三边之间的数量关系.
⒊勾股定理的主要作用是:
在直角三角形中,已知任意两边求第三边的长.
巩固练习
1、如图,在高为3米,斜坡长为5米的楼梯表面铺
地毯,则地毯长度至少需 米.
2、在三角形ABC中, C=90 AC=4,BC=3
求斜边AB边上的高CD。
3、如图:已知AD=14, AB=6, DC=8, BE=EC=y
求AE,ED及y的长。
A
E
D
C
B
6
8
y
y
