1.1 等腰三角形测试题 一课一练(含解析)
文档属性
| 名称 | 1.1 等腰三角形测试题 一课一练(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 388.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-20 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
八下同步课堂【一课一练】(北师大版)
第一章 三角形的证明
第一节 等腰三角形
学校:___________姓名:___________班级:___________总分:___________
一.选择题(共8小题)
1.等腰三角形的两条边长分别为9cm和12cm,则这个等腰三角形的周长是( )
A.30cm B.33cm C.24cm或21cm D.30cm或33cm
2.已知一个等腰三角形一内角的度数为80°,则这个等腰三角形顶角的度数为( )
A.100° B.80° C.50°或80° D.20°或80°
3.用反证法证明“在一个三角形中,至少有一个内角小于或等于60°”时应假设( )
A.三角形中有一个内角小于或等于60°
B.三角形中有两个内角小于或等于60°
C.三角形中有三个内角小于或等于60°
D.三角形中没有一个内角小于或等于60°
4.如图,在△ABC中,∠ABC和∠ACB的平分线相交于点F,过F作DE∥BC,交AB于点D,交AC于点E.若BD=4,DE=7,则线段EC的长为( )
A.3 B.4 C.3.5 D.2
5.在平面直角坐标系中,等腰△ABC的顶点A、B的坐标分别为(0,0)、(2,2),若顶点C落在坐标轴上,则符合条件的点C有( )个.
A.5 B.6 C.7 D.8
6.如图,在△ABC中,∠ACB=90°,D是AB上的点,过点D作DE⊥AB交BC于点F,交AC的延长线于点E,连接CD,∠DCA=∠DAC,则下列结论正确的有( )
①∠DCB=∠B;②CD=AB;③△ADC是等边三角形;④若∠E=30°,则DE=EF+CF.
A.①②③ B.①②④ C.②③④ D.①②③④
7.△ABC中,AB=AC=12厘米,∠B=∠C,BC=8厘米,点D为AB的中点.如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度为v厘米/秒,则当△BPD与△CQP全等时,v的值为( )
A.2 B.5 C.1或5 D.2或3
8.如图,已知△ABC的面积为12,BP平分∠ABC,且AP⊥BP于点P,则△BPC的面积是( )
A.10 B.8 C.6 D.4
二.填空题(共6小题)
9.等腰三角形的一个外角度数为100°,则顶角度数为 .
10.如图,在Rt△ABC中,∠ACB=90°,∠B=30°,CD是斜边AB上的高,AD=3,则线段BD的长为 .
11.已知△ABC为等边三角形,BD为△ABC的高,延长BC至E,使CE=CD=1,连接DE,则BE= ,∠BDE= .
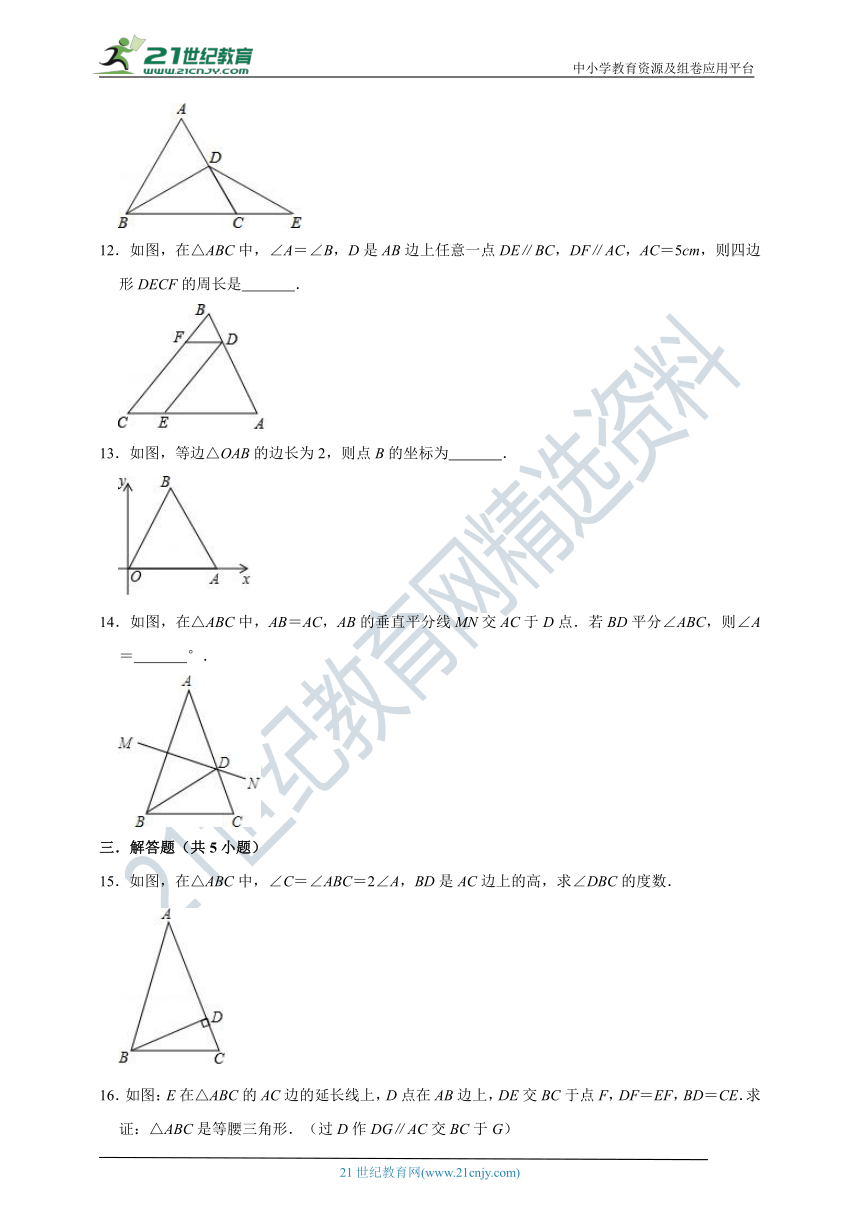
12.如图,在△ABC中,∠A=∠B,D是AB边上任意一点DE∥BC,DF∥AC,AC=5cm,则四边形DECF的周长是 .
13.如图,等边△OAB的边长为2,则点B的坐标为 .
14.如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于D点.若BD平分∠ABC,则∠A= °.
三.解答题(共5小题)
15.如图,在△ABC中,∠C=∠ABC=2∠A,BD是AC边上的高,求∠DBC的度数.
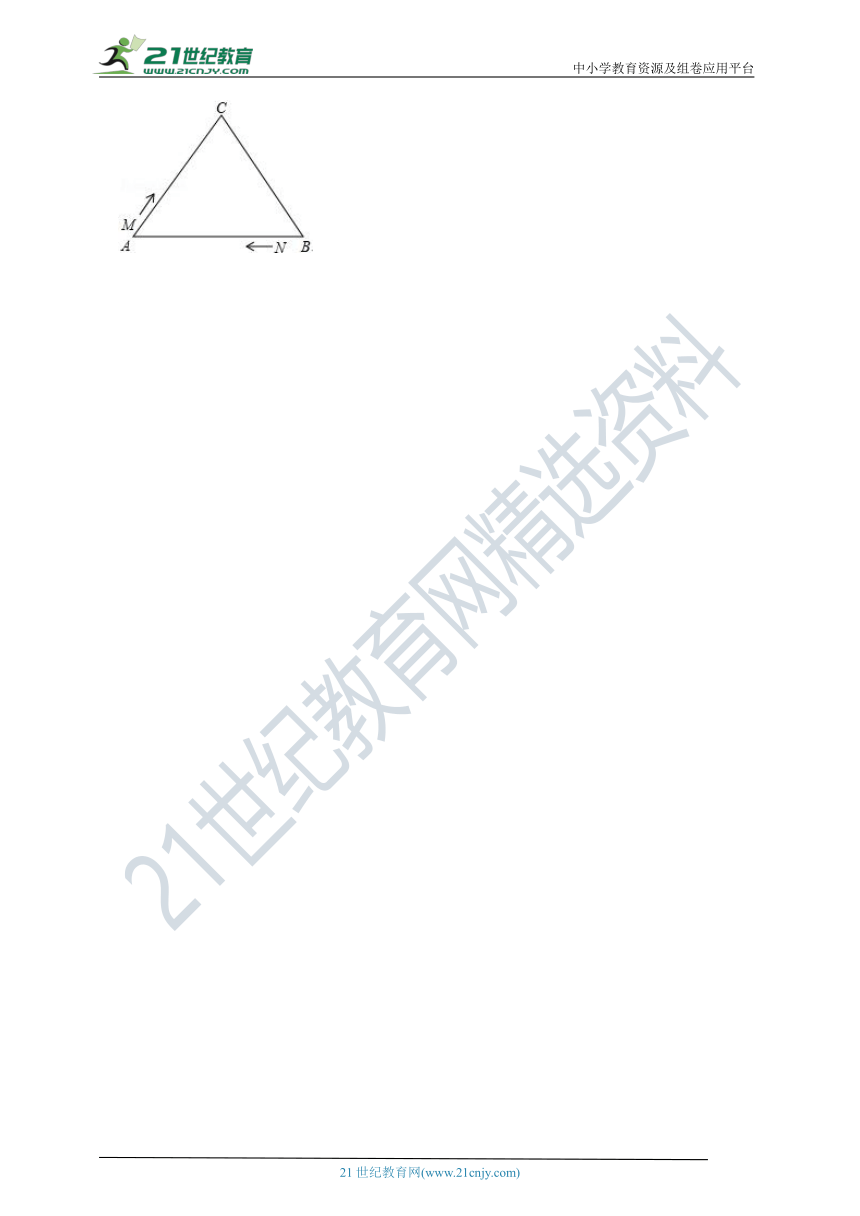
16.如图:E在△ABC的AC边的延长线上,D点在AB边上,DE交BC于点F,DF=EF,BD=CE.求证:△ABC是等腰三角形.(过D作DG∥AC交BC于G)
17.已知:△ABC中,∠B、∠C的角平分线相交于点D,过D作EF∥BC交AB于点E,交AC于点F,求证:BE+CF=EF.
18.如图,在△ABC中,AB=AC,∠BAC=36°,BD是∠ABC的平分线,交AC于点D,E是AB的中点,连接ED并延长,交BC的延长线于点F,连接AF,求证:
(1)EF⊥AB;
(2)△ACF为等腰三角形.
19.如图所示,已知△ABC中,AB=AC=BC=10厘米,M、N分别从点A、点B同时出发,沿三角形的边运动,已知点M的速度是1厘米/秒的速度,点N的速度是2厘米/秒,当点N第一次到达B点时,M、N同时停止运动.
(1)M、N同时运动几秒后,M、N两点重合?
(2)M、N同时运动几秒后,可得等边三角形△AMN?
(3)M、N在BC边上运动时,能否得到以MN为底边的等腰△AMN,如果存在,请求出此时M、N运动的时间?
1.1 等腰三角形
参考答案与试题解析
一.选择题(共8小题)
1.等腰三角形的两条边长分别为9cm和12cm,则这个等腰三角形的周长是( )
A.30cm B.33cm C.24cm或21cm D.30cm或33cm
【解答】解:①当9为腰时,9+9>12,故此三角形的周长=9+9+12=30;
②当12为腰时,9+12>12,故此三角形的周长=9+12+12=33.
故选:D.
2.已知一个等腰三角形一内角的度数为80°,则这个等腰三角形顶角的度数为( )
A.100° B.80° C.50°或80° D.20°或80°
【解答】解:(1)若等腰三角形一个底角为80°,顶角为180°﹣80°﹣80°=20°;
(2)等腰三角形的顶角为80°.
因此这个等腰三角形的顶角的度数为20°或80°.
故选:D.
3.用反证法证明“在一个三角形中,至少有一个内角小于或等于60°”时应假设( )
A.三角形中有一个内角小于或等于60°
B.三角形中有两个内角小于或等于60°
C.三角形中有三个内角小于或等于60°
D.三角形中没有一个内角小于或等于60°
【解答】解:用反证法证明“在一个三角形中,至少有一个内角小于或等于60°”时,
第一步应先假设三角形中没有一个内角小于或等于60°,
故选:D.
4.如图,在△ABC中,∠ABC和∠ACB的平分线相交于点F,过F作DE∥BC,交AB于点D,交AC于点E.若BD=4,DE=7,则线段EC的长为( )
A.3 B.4 C.3.5 D.2
【解答】解:∵∠ABC和∠ACB的平分线相交于点F,
∴∠DBF=∠FBC,∠ECF=∠BCF,
∵DF∥BC,交AB于点D,交AC于点E.
∴∠DFB=∠DBF,∠CFE=∠BCF,
∴BD=DF=4,FE=CE,
∴CE=DE﹣DF=7﹣4=3.
故选:A.
5.在平面直角坐标系中,等腰△ABC的顶点A、B的坐标分别为(0,0)、(2,2),若顶点C落在坐标轴上,则符合条件的点C有( )个.
A.5 B.6 C.7 D.8
【解答】解:①若AC=AB,则以点A为圆心,AB为半径画圆,与坐标轴有4个交点;
②若BC=BA,则以点B为圆心,BA为半径画圆,与坐标轴有2个交点(A点除外);
③若CA=CB,则点C在AB的垂直平分线上,
∵A(0,0),B(2,2),
∴AB的垂直平分线与坐标轴有2个交点.
综上所述:符合条件的点C的个数有8个.
故选:D.
6.如图,在△ABC中,∠ACB=90°,D是AB上的点,过点D作DE⊥AB交BC于点F,交AC的延长线于点E,连接CD,∠DCA=∠DAC,则下列结论正确的有( )
①∠DCB=∠B;②CD=AB;③△ADC是等边三角形;④若∠E=30°,则DE=EF+CF.
A.①②③ B.①②④ C.②③④ D.①②③④
【解答】解:∵在△ABC中,∠ACB=90°,DE⊥AB,
∴∠ADE=∠ACB=90°,
∴∠A+∠B=90°,∠ACD+∠DCB=90°,
∵∠DCA=∠DAC,
∴AD=CD,∠DCB=∠B;故①正确;
∴CD=BD,
∵AD=BD,
∴CD=AB;故②正确;
∠DCA=∠DAC,
∴AD=CD,
但不能判定△ADC是等边三角形;故③错误;
∵若∠E=30°,
∴∠A=60°,
∴△ACD是等边三角形,
∴∠ADC=60°,
∵∠ADE=∠ACB=90°,
∴∠EDC=∠BCD=∠B=30°,
∴CF=DF,
∴DE=EF+DF=EF+CF.故④正确.
故选:B.
7.△ABC中,AB=AC=12厘米,∠B=∠C,BC=8厘米,点D为AB的中点.如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度为v厘米/秒,则当△BPD与△CQP全等时,v的值为( )
A.2 B.5 C.1或5 D.2或3
【解答】解:当BD=PC时,△BPD与△CQP全等,
∵点D为AB的中点,
∴BD=AB=6cm,
∵BD=PC,
∴BP=8﹣6=2(cm),
∵点P在线段BC上以2厘米/秒的速度由B点向C点运动,
∴运动时间时1s,
∵△DBP≌△PCQ,
∴BP=CQ=2cm,
∴v=2÷1=2;
当BD=CQ时,△BDP≌△QCP,
∵BD=6cm,PB=PC,
∴QC=6cm,
∵BC=8cm,
∴BP=4cm,
∴运动时间为4÷2=2(s),
∴v=6÷2=3(m/s).
故v的值为2或3.
故选:D.
8.如图,已知△ABC的面积为12,BP平分∠ABC,且AP⊥BP于点P,则△BPC的面积是( )
A.10 B.8 C.6 D.4
【解答】解:延长AP交BC于E,
∵BP平分∠ABC,
∴∠ABP=∠EBP,
∵AP⊥BP,
∴∠APB=∠EPB=90°,
在△ABP和△EBP中,
,
∴△ABP≌△EBP(ASA),
∴AP=PE,
∴S△ABP=S△EBP,S△ACP=S△ECP,
∴S△PBC=S△ABC=×12=6,
故选:C.
二.填空题(共6小题)
9.等腰三角形的一个外角度数为100°,则顶角度数为 80°或20° .
【解答】解:当100°的角是顶角的外角时,顶角的度数为180°﹣100°=80°;
当100°的角是底角的外角时,底角的度数为180°﹣100°=80°,所以顶角的度数为180°﹣2×80°=20°;
故顶角的度数为80°或20°.
故答案为:80°或20°.
10.如图,在Rt△ABC中,∠ACB=90°,∠B=30°,CD是斜边AB上的高,AD=3,则线段BD的长为 9 .
【解答】解:∵CD⊥AB,∠ACB=90°,
∴∠ADC=90°=∠ACB,
∵∠B=30°,
∴∠A=90°﹣∠B=60°,
∴∠ACD=90°﹣∠A=30°,
∵AD=3,
∴AC=2AD=6,
∴AB=2AC=12,
∴BD=AB﹣AD=12﹣3=9,
故答案为:9.
11.已知△ABC为等边三角形,BD为△ABC的高,延长BC至E,使CE=CD=1,连接DE,则BE= 3 ,∠BDE= 120° .
【解答】解:∵△ABC为等边三角形,
∴∠ABC=∠ACB=60°,AB=BC,∠DCE=120°,
∵BD为高线,
∴∠BDC=90°,∠DBC=∠ABC=30°,
∵CD=CE,
∴∠E=∠CDE,
∵∠E+∠CDE=∠ACB,
∴∠E=30°=∠DBC,
∵∠DCE=120°,
∴∠CDE=180°﹣120°﹣30°=30°,
∴∠BDE=∠BDC+∠CDE=120°,
∵BD是等边三角形ABC的高,CD=1,
∴BC=AC=2CD=2,
∴BE=BC+CE=3,
故答案为:BE=3,∠BDE=120°.
12.如图,在△ABC中,∠A=∠B,D是AB边上任意一点DE∥BC,DF∥AC,AC=5cm,则四边形DECF的周长是 10cm .
【解答】解:∵∠A=∠B,
∴BC=AC=5cm,
∵DF∥AC,
∴∠A=∠BDF,
∵∠A=∠B,
∴∠B=∠BDF,
∴DF=BF,
同理AE=DE,
∴四边形DECF的周长为:CF+DF+DE+CE=CF+BF+AE+CE=BC+AC=5cm+5cm=10cm,
故答案为:10cm.
13.如图,等边△OAB的边长为2,则点B的坐标为 (1,) .
【解答】解:
过B作BD⊥OA于D,则∠BDO=90°,
∵△OAB是等边三角形,
∴OD=AD=OA==1,
在Rt△BDO中,由勾股定理得:BD==,
∴点B的坐标为(1,),
故答案为:(1,).
14.如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于D点.若BD平分∠ABC,则∠A= 36 °.
【解答】解:∵AB=AC,
∴∠C=∠ABC,
∵AB的垂直平分线MN交AC于D点.
∴∠A=∠ABD,
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∴∠C=2∠A=∠ABC,
设∠A为x,
可得:x+x+x+2x=180°,
解得:x=36°,
故答案为:36
三.解答题(共5小题)
15.如图,在△ABC中,∠C=∠ABC=2∠A,BD是AC边上的高,求∠DBC的度数.
【解答】解:∵∠C=∠ABC=2∠A,
∴∠C+∠ABC+∠A=5∠A=180°,
∴∠A=36°.
则∠C=∠ABC=2∠A=72°.
又BD是AC边上的高,
则∠DBC=90°﹣∠C=18°.
16.如图:E在△ABC的AC边的延长线上,D点在AB边上,DE交BC于点F,DF=EF,BD=CE.求证:△ABC是等腰三角形.(过D作DG∥AC交BC于G)
【解答】证明:过点D作DG∥AC交BC于点G,如图所示.
∵DG∥AC,
∴∠GDF=∠E,∠DGB=∠ACB.
在△GDF和△CEF中,,
∴△GDF≌△CEF(ASA),
∴GD=CE.
∵BD=CE,
∴BD=GD,
∴∠B=∠DGB=∠ACB,
∴△ABC是等腰三角形.
17.已知:△ABC中,∠B、∠C的角平分线相交于点D,过D作EF∥BC交AB于点E,交AC于点F,求证:BE+CF=EF.
【解答】证明:∵BD平分∠ABC,
∴∠EBD=∠DBC,
∵EF∥BC,
∴∠EDB=∠DBC,
∴∠EDB=∠EBD,
∴DE=BE,
同理CF=DF,
∴EF=DE+DF=BE+CF,
即BE+CF=EF.
18.如图,在△ABC中,AB=AC,∠BAC=36°,BD是∠ABC的平分线,交AC于点D,E是AB的中点,连接ED并延长,交BC的延长线于点F,连接AF,求证:
(1)EF⊥AB;
(2)△ACF为等腰三角形.
【解答】证明:(1)∵AB=AC,∠BAC=36°,
∴∠ABC=72°,
又∵BD是∠ABC的平分线,
∴∠ABD=36°,
∴∠BAD=∠ABD,
∴AD=BD,
又∵E是AB的中点,
∴DE⊥AB,即FE⊥AB;
(2)∵FE⊥AB,AE=BE,
∴FE垂直平分AB,
∴AF=BF,
∴∠BAF=∠ABF,
又∵∠ABD=∠BAD,
∴∠FAD=∠FBD=36°,
又∵∠ACB=72°,
∴∠AFC=∠ACB﹣∠CAF=36°,
∴∠CAF=∠AFC=36°,
∴AC=CF,即△ACF为等腰三角形.
19.如图所示,已知△ABC中,AB=AC=BC=10厘米,M、N分别从点A、点B同时出发,沿三角形的边运动,已知点M的速度是1厘米/秒的速度,点N的速度是2厘米/秒,当点N第一次到达B点时,M、N同时停止运动.
(1)M、N同时运动几秒后,M、N两点重合?
(2)M、N同时运动几秒后,可得等边三角形△AMN?
(3)M、N在BC边上运动时,能否得到以MN为底边的等腰△AMN,如果存在,请求出此时M、N运动的时间?
【解答】解:(1)设点M、N运动x秒后,M、N两点重合,
x×1+10=2x,
解得:x=10;
(2)设点M、N运动t秒后,可得到等边三角形△AMN,如图①,
AM=t×1=t,AN=AB﹣BN=10﹣2t,
∵三角形△AMN是等边三角形,
∴t=10﹣2t,
解得t=,
∴点M、N运动秒后,可得到等边三角形△AMN.
(3)当点M、N在BC边上运动时,可以得到以MN为底边的等腰三角形,
由(1)知10秒时M、N两点重合,恰好在C处,
如图②,假设△AMN是等腰三角形,
∴AN=AM,
∴∠AMN=∠ANM,
∴∠AMC=∠ANB,
∵AB=BC=AC,
∴△ACB是等边三角形,
∴∠C=∠B,
在△ACM和△ABN中,
∵,
∴△ACM≌△ABN(AAS),
∴CM=BN,
设当点M、N在BC边上运动时,M、N运动的时间y秒时,△AMN是等腰三角形,
∴CM=y﹣10,NB=30﹣2y,CM=NB,
y﹣10=30﹣2y,
解得:y=.故假设成立.
∴当点M、N在BC边上运动时,能得到以MN为底边的等腰△AMN,此时M、N运动的时间为秒.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
