2020春华师大版九下数学27.2.2直线与圆的位置关系同步课堂练习含答案
文档属性
| 名称 | 2020春华师大版九下数学27.2.2直线与圆的位置关系同步课堂练习含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 989.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-20 00:00:00 | ||
图片预览



文档简介
2020春华师大版九下数学27.2.2直线与圆的位置关系同步课堂练习(学生版)
基础题
知识点 直线与圆的位置关系
1.已知⊙O的半径是5 cm,点O到同一平面内直线l的距离为5 cm,则直线l与⊙O的位置关系是( )
A.相交 B.相切
C.相离 D.无法确定
2.已知⊙O的半径为5,圆心O到直线l的距离为3,则反映直线l与⊙O的位置关系的图形是( )
3.已知一条直线与圆有公共点,则这条直线与圆的位置关系是( )
A.相离 B.相切
C.相交 D.相切或相交
4.直线l与半径为r的⊙O相交,且点O到直线l的距离为5,则半径r的取值范围是( )
A.r>5 B.r=5
C.05.在平面直角坐标系xOy中,以点(-3,4)为圆心,4为半径的圆( )
A.与x轴相交,与y轴相切
B.与x轴相离,与y轴相交
C.与x轴相切,与y轴相交
D.与x轴相切,与y轴相离
6.已知圆的直径为10 cm,圆心到直线l的距离为5 cm,那么l和这个圆有 个公共点.
7.如图,若把太阳看成一个圆,则太阳与地平线l的位置关系是 .
8.如图,已知∠BOA=30°,M为OB边上一点,以M为圆心,2 cm为半径作⊙M.点M在射线OB上运动,当OM=5 cm时,⊙M与直线OA的位置关系是 .
9.(教材P50例1变式)如图,在Rt△ABC中,∠C=90°,AB=4 cm,BC=2 cm,以C为圆心,r为半径的圆与直线AB有何种位置关系?请你写出判断过程.
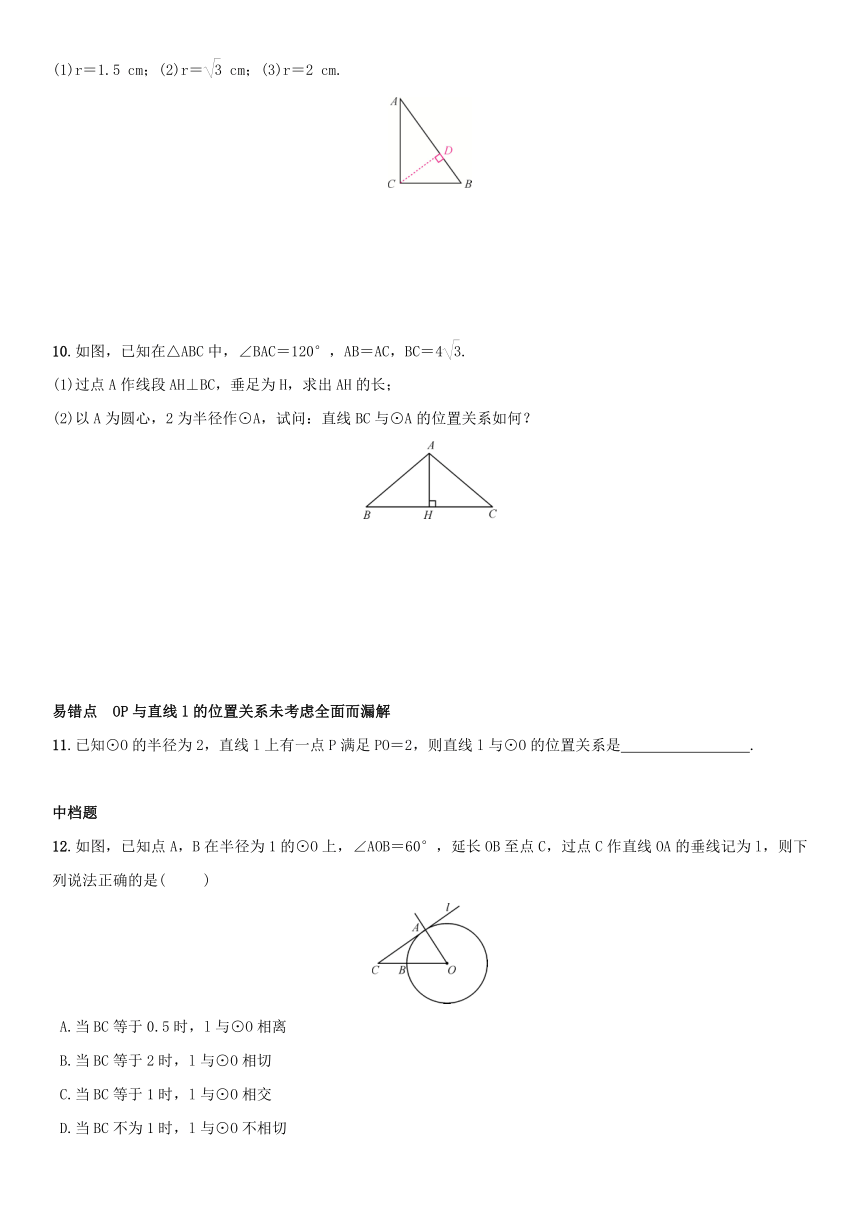
(1)r=1.5 cm;(2)r= cm;(3)r=2 cm.
10.如图,已知在△ABC中,∠BAC=120°,AB=AC,BC=4.
(1)过点A作线段AH⊥BC,垂足为H,求出AH的长;
(2)以A为圆心,2为半径作⊙A,试问:直线BC与⊙A的位置关系如何?
易错点 OP与直线l的位置关系未考虑全面而漏解
11.已知⊙O的半径为2,直线l上有一点P满足PO=2,则直线l与⊙O的位置关系是 .
中档题
12.如图,已知点A,B在半径为1的⊙O上,∠AOB=60°,延长OB至点C,过点C作直线OA的垂线记为l,则下列说法正确的是( )
A.当BC等于0.5时,l与⊙O相离
B.当BC等于2时,l与⊙O相切
C.当BC等于1时,l与⊙O相交
D.当BC不为1时,l与⊙O不相切
13.如图,在平面直角坐标系中,半径为2的⊙P的圆心P的坐标为(-3,0),将⊙P沿x轴的正方向平移,使得⊙P与y轴相切,则平移的距离为( )
A.1 B.3
C.5 D.1或5
14.如图,点P为⊙O外一点,连结OP交⊙O于点Q,且PQ=OQ,经过点P的直线l1,l2都与⊙O相交,则l1与l2所成的锐角α的取值范围是( )
A.0°<α<30°
B.0°<α<45°
C.0°<α<60°
D.0°<α<90°
15.⊙O的半径为R,点O到直线l的距离为d,R,d是方程x2-4x+m=0的两根,当直线l与⊙O相切时,m的值为 .
16.已知直线y=kx(k≠0)经过点(12,-5),将直线向上平移m(m>0)个单位长度.若平移后得到的直线与半径为6的⊙O相交(点O为坐标原点),则m的取值范围为 .
17.如图,给定一个半径长为2的圆,圆心O到水平直线l的距离为d,即OM=d.我们把圆上到直线l的距离等于1的点的个数记为m.如d=0时,l为经过圆心O的一条直线,此时圆上有四个到直线l的距离等于1的点,即m=4,由此可知:
(1)当d=3时,m= ;
(2)当m=2时,d的取值范围是 .
18.如图,在Rt△ABC中,∠C=90°,∠A=30°,O为AB上一点,BO=x,⊙O的半径为2.
(1)当x为何值时,直线BC与⊙O相切?
(2)当x分别在什么范围内取值时,直线BC与⊙O相离、相交?
综合题
19.如图,已知在?ABCD中,AB=5,BC=8,cosB=,点E是BC边上的动点,当以CE为半径的⊙C与边AD不相交时,求半径CE的取值范围.
2020春华师大版九下数学27.2.2直线与圆的位置关系同步课堂练习(教师版)
基础题
知识点 直线与圆的位置关系
1.已知⊙O的半径是5 cm,点O到同一平面内直线l的距离为5 cm,则直线l与⊙O的位置关系是(B)
A.相交 B.相切
C.相离 D.无法确定
2.已知⊙O的半径为5,圆心O到直线l的距离为3,则反映直线l与⊙O的位置关系的图形是(B)
3.已知一条直线与圆有公共点,则这条直线与圆的位置关系是(D)
A.相离 B.相切
C.相交 D.相切或相交
4.直线l与半径为r的⊙O相交,且点O到直线l的距离为5,则半径r的取值范围是(A)
A.r>5 B.r=5
C.05.在平面直角坐标系xOy中,以点(-3,4)为圆心,4为半径的圆(C)
A.与x轴相交,与y轴相切
B.与x轴相离,与y轴相交
C.与x轴相切,与y轴相交
D.与x轴相切,与y轴相离
6.已知圆的直径为10 cm,圆心到直线l的距离为5 cm,那么l和这个圆有1个公共点.
7.如图,若把太阳看成一个圆,则太阳与地平线l的位置关系是相离.
8.如图,已知∠BOA=30°,M为OB边上一点,以M为圆心,2 cm为半径作⊙M.点M在射线OB上运动,当OM=5 cm时,⊙M与直线OA的位置关系是相离.
9.(教材P50例1变式)如图,在Rt△ABC中,∠C=90°,AB=4 cm,BC=2 cm,以C为圆心,r为半径的圆与直线AB有何种位置关系?请你写出判断过程.
(1)r=1.5 cm;(2)r= cm;(3)r=2 cm.
解:过点C作CD⊥AB,垂足为D.
∵AB=4 cm,BC=2 cm,
∴AC=2 cm.
又∵S△ABC=AB·CD=BC·AC,∴CD== cm.
(1)r=1.5 cm时,相离;
(2)r= cm时,相切;
(3)r=2 cm时,相交.
10.如图,已知在△ABC中,∠BAC=120°,AB=AC,BC=4.
(1)过点A作线段AH⊥BC,垂足为H,求出AH的长;
(2)以A为圆心,2为半径作⊙A,试问:直线BC与⊙A的位置关系如何?
解:(1)∵∠BAC=120°,AB=AC,AH⊥BC,BC=4,
∴∠AHB=90°,∠B=30°,BH=2.
在Rt△AHB中,tanB==,
∴AH=2.
(2)由(1)知AH=2,
∵⊙A以A为圆心,2为半径,
∴直线BC与⊙A相切.
易错点 OP与直线l的位置关系未考虑全面而漏解
11.已知⊙O的半径为2,直线l上有一点P满足PO=2,则直线l与⊙O的位置关系是相切或相交.
中档题
12.如图,已知点A,B在半径为1的⊙O上,∠AOB=60°,延长OB至点C,过点C作直线OA的垂线记为l,则下列说法正确的是(D)
A.当BC等于0.5时,l与⊙O相离
B.当BC等于2时,l与⊙O相切
C.当BC等于1时,l与⊙O相交
D.当BC不为1时,l与⊙O不相切
13.如图,在平面直角坐标系中,半径为2的⊙P的圆心P的坐标为(-3,0),将⊙P沿x轴的正方向平移,使得⊙P与y轴相切,则平移的距离为(D)
A.1 B.3
C.5 D.1或5
14.如图,点P为⊙O外一点,连结OP交⊙O于点Q,且PQ=OQ,经过点P的直线l1,l2都与⊙O相交,则l1与l2所成的锐角α的取值范围是(C)
A.0°<α<30°
B.0°<α<45°
C.0°<α<60°
D.0°<α<90°
15.⊙O的半径为R,点O到直线l的距离为d,R,d是方程x2-4x+m=0的两根,当直线l与⊙O相切时,m的值为4.
16.已知直线y=kx(k≠0)经过点(12,-5),将直线向上平移m(m>0)个单位长度.若平移后得到的直线与半径为6的⊙O相交(点O为坐标原点),则m的取值范围为0
17.如图,给定一个半径长为2的圆,圆心O到水平直线l的距离为d,即OM=d.我们把圆上到直线l的距离等于1的点的个数记为m.如d=0时,l为经过圆心O的一条直线,此时圆上有四个到直线l的距离等于1的点,即m=4,由此可知:
(1)当d=3时,m=1;
(2)当m=2时,d的取值范围是1<d<3.
18.如图,在Rt△ABC中,∠C=90°,∠A=30°,O为AB上一点,BO=x,⊙O的半径为2.
(1)当x为何值时,直线BC与⊙O相切?
(2)当x分别在什么范围内取值时,直线BC与⊙O相离、相交?
解:(1)作OD∥AC,交BC于点D,
∵∠C=90°,∠A=30°,
∴∠ODB=90°,∠DOB=30°.
∵BO=x,OD=2,
∴cos30°=.
解得x=.
∴当x=时,直线BC与⊙O相切.
(2)①若⊙O与直线BC相离,则x>;
②若⊙O与直线BC相交,则x<.
综合题
19.如图,已知在?ABCD中,AB=5,BC=8,cosB=,点E是BC边上的动点,当以CE为半径的⊙C与边AD不相交时,求半径CE的取值范围.
解:过点A作AM⊥BC于点M,过点C作CN⊥AD于点N,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD=5.∴AM=CN.
∵AB=5,cosB==,∴BM=4.
在Rt△ABM中,由勾股定理,得
AM=CN==3.
∵BC=8,BM=4,
∴CM=4.
∴在Rt△ACM中,AC==5.
∴当以CE为半径的⊙C与边AD不相交时,半径CE的取值范围是0<CE<3或5<CE≤8.
基础题
知识点 直线与圆的位置关系
1.已知⊙O的半径是5 cm,点O到同一平面内直线l的距离为5 cm,则直线l与⊙O的位置关系是( )
A.相交 B.相切
C.相离 D.无法确定
2.已知⊙O的半径为5,圆心O到直线l的距离为3,则反映直线l与⊙O的位置关系的图形是( )
3.已知一条直线与圆有公共点,则这条直线与圆的位置关系是( )
A.相离 B.相切
C.相交 D.相切或相交
4.直线l与半径为r的⊙O相交,且点O到直线l的距离为5,则半径r的取值范围是( )
A.r>5 B.r=5
C.0
A.与x轴相交,与y轴相切
B.与x轴相离,与y轴相交
C.与x轴相切,与y轴相交
D.与x轴相切,与y轴相离
6.已知圆的直径为10 cm,圆心到直线l的距离为5 cm,那么l和这个圆有 个公共点.
7.如图,若把太阳看成一个圆,则太阳与地平线l的位置关系是 .
8.如图,已知∠BOA=30°,M为OB边上一点,以M为圆心,2 cm为半径作⊙M.点M在射线OB上运动,当OM=5 cm时,⊙M与直线OA的位置关系是 .
9.(教材P50例1变式)如图,在Rt△ABC中,∠C=90°,AB=4 cm,BC=2 cm,以C为圆心,r为半径的圆与直线AB有何种位置关系?请你写出判断过程.
(1)r=1.5 cm;(2)r= cm;(3)r=2 cm.
10.如图,已知在△ABC中,∠BAC=120°,AB=AC,BC=4.
(1)过点A作线段AH⊥BC,垂足为H,求出AH的长;
(2)以A为圆心,2为半径作⊙A,试问:直线BC与⊙A的位置关系如何?
易错点 OP与直线l的位置关系未考虑全面而漏解
11.已知⊙O的半径为2,直线l上有一点P满足PO=2,则直线l与⊙O的位置关系是 .
中档题
12.如图,已知点A,B在半径为1的⊙O上,∠AOB=60°,延长OB至点C,过点C作直线OA的垂线记为l,则下列说法正确的是( )
A.当BC等于0.5时,l与⊙O相离
B.当BC等于2时,l与⊙O相切
C.当BC等于1时,l与⊙O相交
D.当BC不为1时,l与⊙O不相切
13.如图,在平面直角坐标系中,半径为2的⊙P的圆心P的坐标为(-3,0),将⊙P沿x轴的正方向平移,使得⊙P与y轴相切,则平移的距离为( )
A.1 B.3
C.5 D.1或5
14.如图,点P为⊙O外一点,连结OP交⊙O于点Q,且PQ=OQ,经过点P的直线l1,l2都与⊙O相交,则l1与l2所成的锐角α的取值范围是( )
A.0°<α<30°
B.0°<α<45°
C.0°<α<60°
D.0°<α<90°
15.⊙O的半径为R,点O到直线l的距离为d,R,d是方程x2-4x+m=0的两根,当直线l与⊙O相切时,m的值为 .
16.已知直线y=kx(k≠0)经过点(12,-5),将直线向上平移m(m>0)个单位长度.若平移后得到的直线与半径为6的⊙O相交(点O为坐标原点),则m的取值范围为 .
17.如图,给定一个半径长为2的圆,圆心O到水平直线l的距离为d,即OM=d.我们把圆上到直线l的距离等于1的点的个数记为m.如d=0时,l为经过圆心O的一条直线,此时圆上有四个到直线l的距离等于1的点,即m=4,由此可知:
(1)当d=3时,m= ;
(2)当m=2时,d的取值范围是 .
18.如图,在Rt△ABC中,∠C=90°,∠A=30°,O为AB上一点,BO=x,⊙O的半径为2.
(1)当x为何值时,直线BC与⊙O相切?
(2)当x分别在什么范围内取值时,直线BC与⊙O相离、相交?
综合题
19.如图,已知在?ABCD中,AB=5,BC=8,cosB=,点E是BC边上的动点,当以CE为半径的⊙C与边AD不相交时,求半径CE的取值范围.
2020春华师大版九下数学27.2.2直线与圆的位置关系同步课堂练习(教师版)
基础题
知识点 直线与圆的位置关系
1.已知⊙O的半径是5 cm,点O到同一平面内直线l的距离为5 cm,则直线l与⊙O的位置关系是(B)
A.相交 B.相切
C.相离 D.无法确定
2.已知⊙O的半径为5,圆心O到直线l的距离为3,则反映直线l与⊙O的位置关系的图形是(B)
3.已知一条直线与圆有公共点,则这条直线与圆的位置关系是(D)
A.相离 B.相切
C.相交 D.相切或相交
4.直线l与半径为r的⊙O相交,且点O到直线l的距离为5,则半径r的取值范围是(A)
A.r>5 B.r=5
C.0
A.与x轴相交,与y轴相切
B.与x轴相离,与y轴相交
C.与x轴相切,与y轴相交
D.与x轴相切,与y轴相离
6.已知圆的直径为10 cm,圆心到直线l的距离为5 cm,那么l和这个圆有1个公共点.
7.如图,若把太阳看成一个圆,则太阳与地平线l的位置关系是相离.
8.如图,已知∠BOA=30°,M为OB边上一点,以M为圆心,2 cm为半径作⊙M.点M在射线OB上运动,当OM=5 cm时,⊙M与直线OA的位置关系是相离.
9.(教材P50例1变式)如图,在Rt△ABC中,∠C=90°,AB=4 cm,BC=2 cm,以C为圆心,r为半径的圆与直线AB有何种位置关系?请你写出判断过程.
(1)r=1.5 cm;(2)r= cm;(3)r=2 cm.
解:过点C作CD⊥AB,垂足为D.
∵AB=4 cm,BC=2 cm,
∴AC=2 cm.
又∵S△ABC=AB·CD=BC·AC,∴CD== cm.
(1)r=1.5 cm时,相离;
(2)r= cm时,相切;
(3)r=2 cm时,相交.
10.如图,已知在△ABC中,∠BAC=120°,AB=AC,BC=4.
(1)过点A作线段AH⊥BC,垂足为H,求出AH的长;
(2)以A为圆心,2为半径作⊙A,试问:直线BC与⊙A的位置关系如何?
解:(1)∵∠BAC=120°,AB=AC,AH⊥BC,BC=4,
∴∠AHB=90°,∠B=30°,BH=2.
在Rt△AHB中,tanB==,
∴AH=2.
(2)由(1)知AH=2,
∵⊙A以A为圆心,2为半径,
∴直线BC与⊙A相切.
易错点 OP与直线l的位置关系未考虑全面而漏解
11.已知⊙O的半径为2,直线l上有一点P满足PO=2,则直线l与⊙O的位置关系是相切或相交.
中档题
12.如图,已知点A,B在半径为1的⊙O上,∠AOB=60°,延长OB至点C,过点C作直线OA的垂线记为l,则下列说法正确的是(D)
A.当BC等于0.5时,l与⊙O相离
B.当BC等于2时,l与⊙O相切
C.当BC等于1时,l与⊙O相交
D.当BC不为1时,l与⊙O不相切
13.如图,在平面直角坐标系中,半径为2的⊙P的圆心P的坐标为(-3,0),将⊙P沿x轴的正方向平移,使得⊙P与y轴相切,则平移的距离为(D)
A.1 B.3
C.5 D.1或5
14.如图,点P为⊙O外一点,连结OP交⊙O于点Q,且PQ=OQ,经过点P的直线l1,l2都与⊙O相交,则l1与l2所成的锐角α的取值范围是(C)
A.0°<α<30°
B.0°<α<45°
C.0°<α<60°
D.0°<α<90°
15.⊙O的半径为R,点O到直线l的距离为d,R,d是方程x2-4x+m=0的两根,当直线l与⊙O相切时,m的值为4.
16.已知直线y=kx(k≠0)经过点(12,-5),将直线向上平移m(m>0)个单位长度.若平移后得到的直线与半径为6的⊙O相交(点O为坐标原点),则m的取值范围为0
17.如图,给定一个半径长为2的圆,圆心O到水平直线l的距离为d,即OM=d.我们把圆上到直线l的距离等于1的点的个数记为m.如d=0时,l为经过圆心O的一条直线,此时圆上有四个到直线l的距离等于1的点,即m=4,由此可知:
(1)当d=3时,m=1;
(2)当m=2时,d的取值范围是1<d<3.
18.如图,在Rt△ABC中,∠C=90°,∠A=30°,O为AB上一点,BO=x,⊙O的半径为2.
(1)当x为何值时,直线BC与⊙O相切?
(2)当x分别在什么范围内取值时,直线BC与⊙O相离、相交?
解:(1)作OD∥AC,交BC于点D,
∵∠C=90°,∠A=30°,
∴∠ODB=90°,∠DOB=30°.
∵BO=x,OD=2,
∴cos30°=.
解得x=.
∴当x=时,直线BC与⊙O相切.
(2)①若⊙O与直线BC相离,则x>;
②若⊙O与直线BC相交,则x<.
综合题
19.如图,已知在?ABCD中,AB=5,BC=8,cosB=,点E是BC边上的动点,当以CE为半径的⊙C与边AD不相交时,求半径CE的取值范围.
解:过点A作AM⊥BC于点M,过点C作CN⊥AD于点N,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD=5.∴AM=CN.
∵AB=5,cosB==,∴BM=4.
在Rt△ABM中,由勾股定理,得
AM=CN==3.
∵BC=8,BM=4,
∴CM=4.
∴在Rt△ACM中,AC==5.
∴当以CE为半径的⊙C与边AD不相交时,半径CE的取值范围是0<CE<3或5<CE≤8.
