2020春华师大版九下数学27.1.3圆周角第1课时圆周角定理同步课堂练习含答案
文档属性
| 名称 | 2020春华师大版九下数学27.1.3圆周角第1课时圆周角定理同步课堂练习含答案 |
|
|
| 格式 | zip | ||
| 文件大小 | 192.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-20 13:36:23 | ||
图片预览


文档简介
2020春华师大版九下数学27.1.3圆周角第1课时圆周角定理同步课堂练习(学生版)
基础题
知识点1 半圆或直径所对的圆周角都相等,都等于90°(直角)
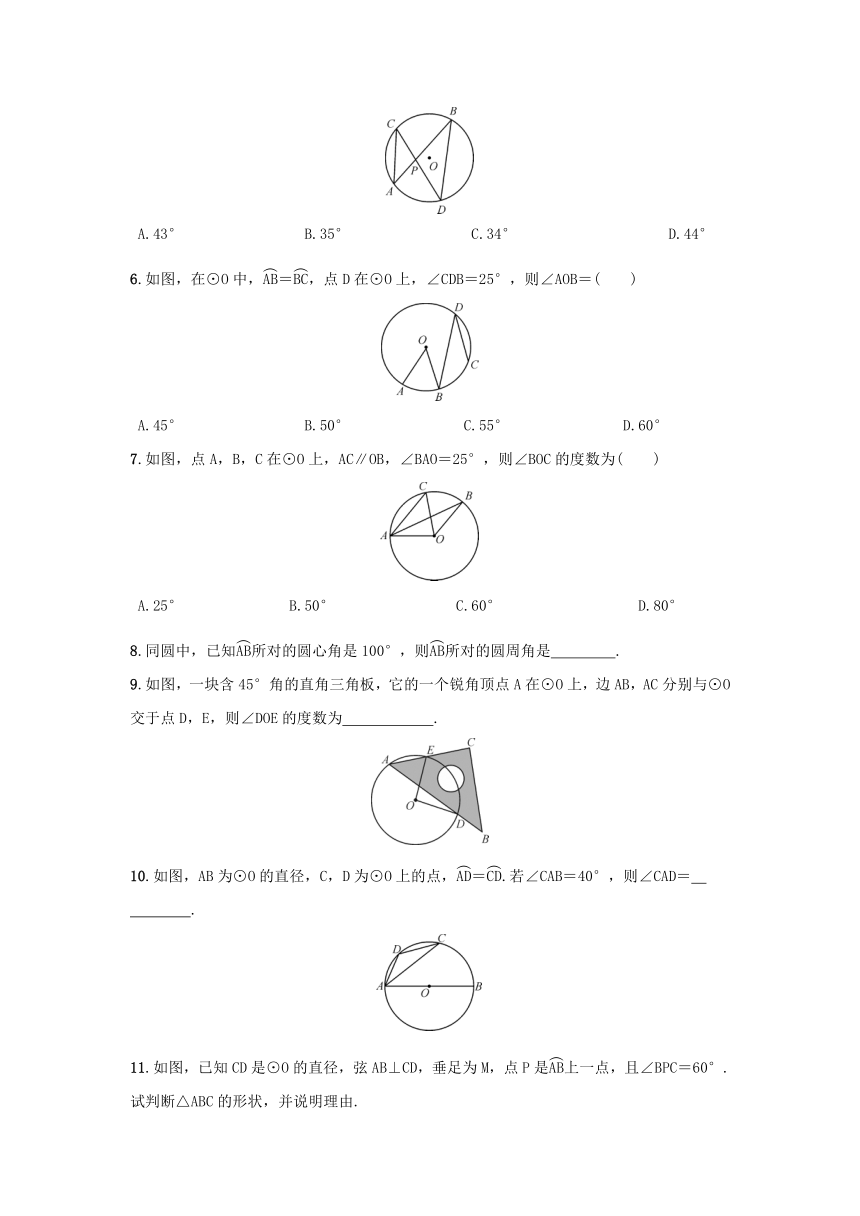
1.如图,BC是⊙O的直径,点A是⊙O上异于B,C的一点,则∠A的度数为( )
A.60° B.70° C.80° D.90°
2.如图,BC是⊙O的直径,A是⊙O上的一点,∠OAC=32°,则∠B的度数是( )
A.58° B.60° C.64° D.68°
3.如图,AB为⊙O的直径,点C,D在⊙O上,且BC=6 cm,AC=8 cm,∠ABD=45°.求BD的长.
知识点2 圆周角定理
4.如图,⊙O是△ABC的外接圆,∠BOC=120°,则∠BAC的度数是( )
A.120° B.80° C.60° D.30°
5.如图,在⊙O中,弦AB,CD相交于点P,∠A=42°,∠APD=77°,则∠B的大小是( )
A.43° B.35° C.34° D.44°
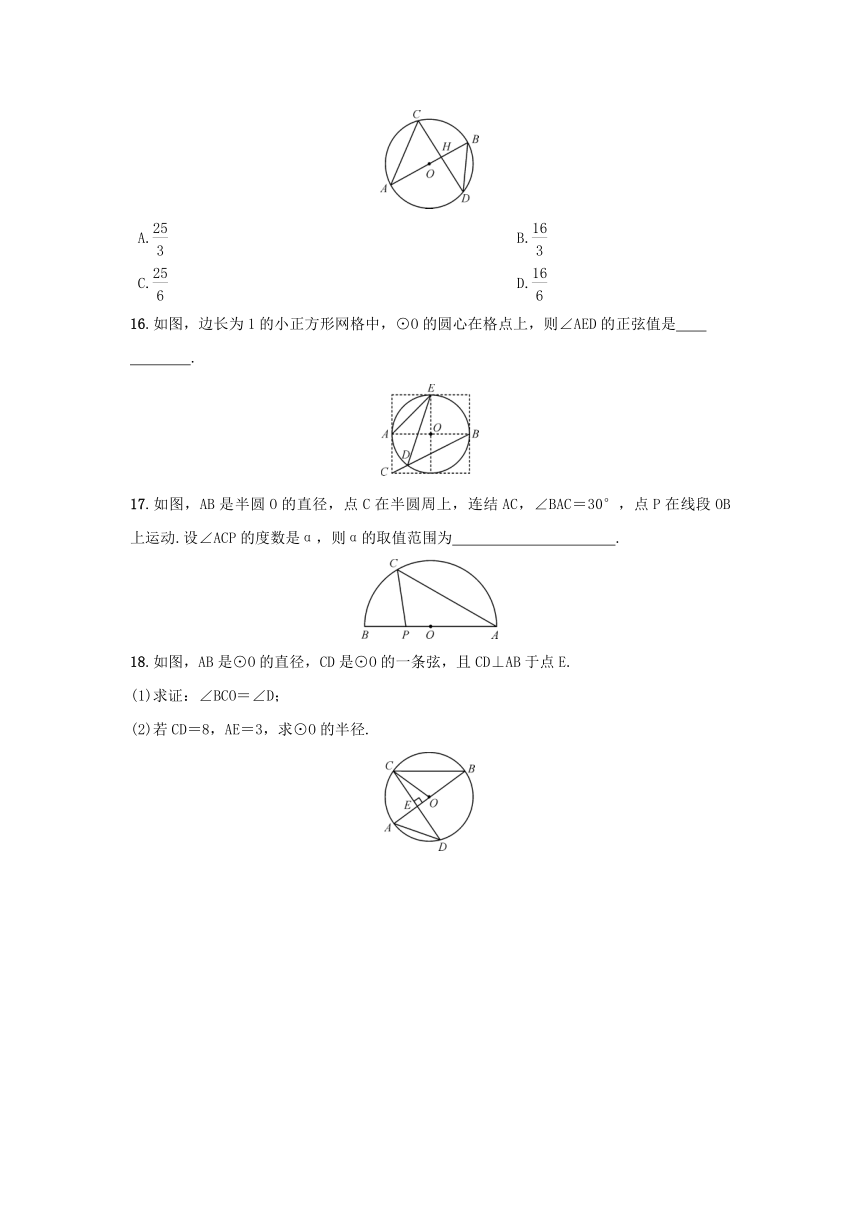
6.如图,在⊙O中,=,点D在⊙O上,∠CDB=25°,则∠AOB=( )
A.45° B.50° C.55° D.60°
7.如图,点A,B,C在⊙O上,AC∥OB,∠BAO=25°,则∠BOC的度数为( )
A.25° B.50° C.60° D.80°
8.同圆中,已知所对的圆心角是100°,则所对的圆周角是 .
9.如图,一块含45°角的直角三角板,它的一个锐角顶点A在⊙O上,边AB,AC分别与⊙O交于点D,E,则∠DOE的度数为 .
10.如图,AB为⊙O的直径,C,D为⊙O上的点,=.若∠CAB=40°,则∠CAD= .
11.如图,已知CD是⊙O的直径,弦AB⊥CD,垂足为M,点P是上一点,且∠BPC=60°.试判断△ABC的形状,并说明理由.
易错点 忽略弦所对的圆周角不唯一而致错
12.已知BC是半径为2 cm的圆内的一条弦,点A为圆上除点B,C外任意一点.若BC=2 cm,则∠BAC的度数为 .
中档题
13.如图,在⊙O中,AE是直径,半径OC垂直于弦AB于点D,连结BE.若AB=2,CD=1,则BE的长是( )
A.5 B.6
C.7 D.8
14.如图,⊙O是△ABC的外接圆,∠B=60°,OP⊥AC于点P,OP=4,则⊙O的半径为( )
A.8 B.12 C.8 D.12
15.如图,AB是⊙O的直径,且经过弦CD的中点H,已知sin∠CDB=,BD=5,则AH的长度为( )
A. B.
C. D.
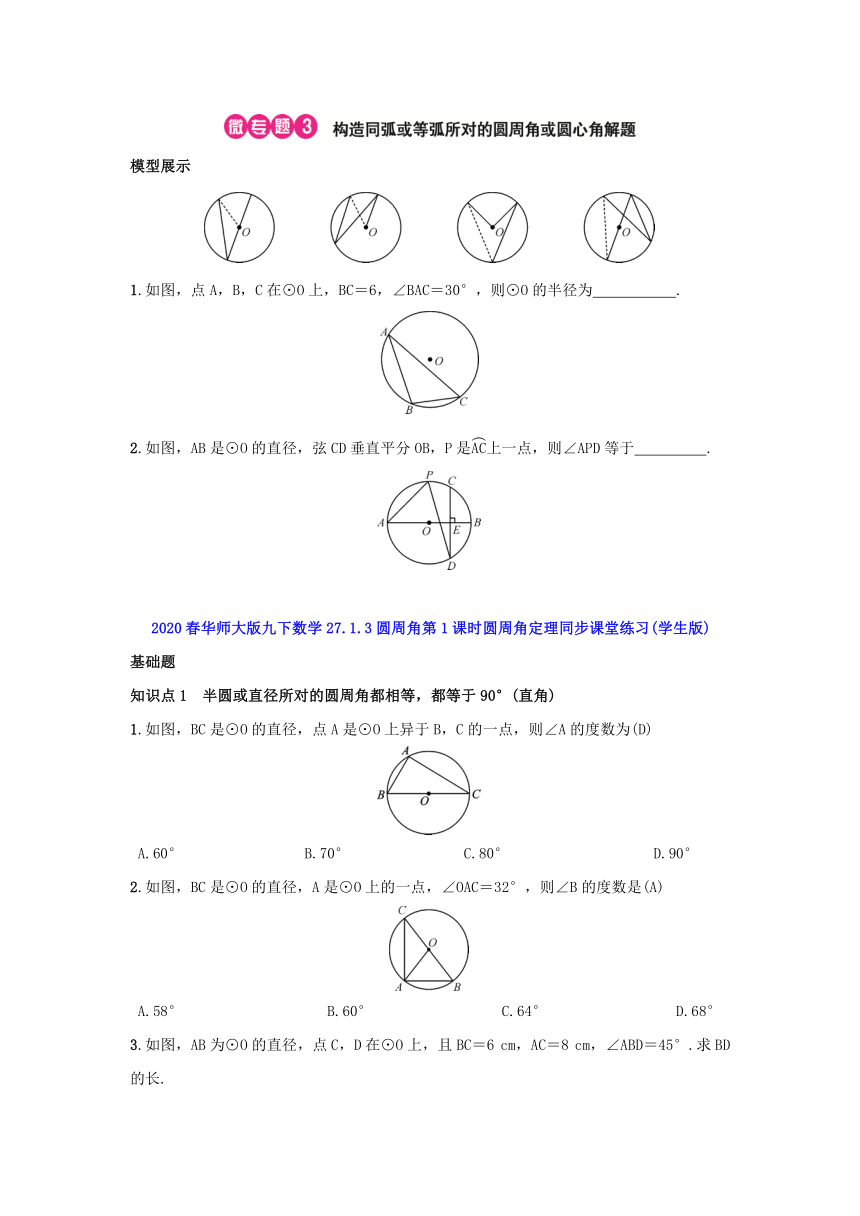
16.如图,边长为1的小正方形网格中,⊙O的圆心在格点上,则∠AED的正弦值是 .
17.如图,AB是半圆O的直径,点C在半圆周上,连结AC,∠BAC=30°,点P在线段OB上运动.设∠ACP的度数是α,则α的取值范围为 .
18.如图,AB是⊙O的直径,CD是⊙O的一条弦,且CD⊥AB于点E.
(1)求证:∠BCO=∠D;
(2)若CD=8,AE=3,求⊙O的半径.
模型展示
1.如图,点A,B,C在⊙O上,BC=6,∠BAC=30°,则⊙O的半径为 .
2.如图,AB是⊙O的直径,弦CD垂直平分OB,P是上一点,则∠APD等于 .
2020春华师大版九下数学27.1.3圆周角第1课时圆周角定理同步课堂练习(学生版)
基础题
知识点1 半圆或直径所对的圆周角都相等,都等于90°(直角)
1.如图,BC是⊙O的直径,点A是⊙O上异于B,C的一点,则∠A的度数为(D)
A.60° B.70° C.80° D.90°
2.如图,BC是⊙O的直径,A是⊙O上的一点,∠OAC=32°,则∠B的度数是(A)
A.58° B.60° C.64° D.68°
3.如图,AB为⊙O的直径,点C,D在⊙O上,且BC=6 cm,AC=8 cm,∠ABD=45°.求BD的长.
解:连结OD.
∵AB为⊙O的直径,
∴∠ACB=90°.
∵BC=6 cm,AC=8 cm,
∴AB=10 cm.
∴OB=5 cm.
∵OD=OB,
∴∠ODB=∠ABD=45°.
∴∠BOD=90°.
∴BD==5 cm.
知识点2 圆周角定理
4.如图,⊙O是△ABC的外接圆,∠BOC=120°,则∠BAC的度数是(C)
A.120° B.80° C.60° D.30°
5.如图,在⊙O中,弦AB,CD相交于点P,∠A=42°,∠APD=77°,则∠B的大小是(B)
A.43° B.35° C.34° D.44°
6.如图,在⊙O中,=,点D在⊙O上,∠CDB=25°,则∠AOB=(B)
A.45° B.50° C.55° D.60°
7.如图,点A,B,C在⊙O上,AC∥OB,∠BAO=25°,则∠BOC的度数为(B)
A.25° B.50° C.60° D.80°
8.同圆中,已知所对的圆心角是100°,则所对的圆周角是50°.
9.如图,一块含45°角的直角三角板,它的一个锐角顶点A在⊙O上,边AB,AC分别与⊙O交于点D,E,则∠DOE的度数为90°.
10.如图,AB为⊙O的直径,C,D为⊙O上的点,=.若∠CAB=40°,则∠CAD=25°.
11.如图,已知CD是⊙O的直径,弦AB⊥CD,垂足为M,点P是上一点,且∠BPC=60°.试判断△ABC的形状,并说明理由.
解:△ABC为等边三角形.
理由:∵AB⊥CD,CD为⊙O的直径,
∴=.
∴AC=BC.
又∵∠BPC=∠A=60°,
∴△ABC为等边三角形.
易错点 忽略弦所对的圆周角不唯一而致错
12.已知BC是半径为2 cm的圆内的一条弦,点A为圆上除点B,C外任意一点.若BC=2 cm,则∠BAC的度数为60°或120°.
中档题
13.如图,在⊙O中,AE是直径,半径OC垂直于弦AB于点D,连结BE.若AB=2,CD=1,则BE的长是(B)
A.5 B.6
C.7 D.8
14.如图,⊙O是△ABC的外接圆,∠B=60°,OP⊥AC于点P,OP=4,则⊙O的半径为(C)
A.8 B.12 C.8 D.12
15.如图,AB是⊙O的直径,且经过弦CD的中点H,已知sin∠CDB=,BD=5,则AH的长度为(B)
A. B.
C. D.
16.如图,边长为1的小正方形网格中,⊙O的圆心在格点上,则∠AED的正弦值是.
17.如图,AB是半圆O的直径,点C在半圆周上,连结AC,∠BAC=30°,点P在线段OB上运动.设∠ACP的度数是α,则α的取值范围为30°≤α≤90°.
18.如图,AB是⊙O的直径,CD是⊙O的一条弦,且CD⊥AB于点E.
(1)求证:∠BCO=∠D;
(2)若CD=8,AE=3,求⊙O的半径.
解:(1)证明:∵OB=OC,
∴∠BCO=∠B.
∵∠B=∠D,
∴∠BCO=∠D.
(2)∵AB是⊙O的直径,CD⊥AB,
∴CE=DE=CD=×8=4.
∵∠B=∠D,∠BEC=∠DEA,
∴△BCE∽△DAE.
∴AE∶CE=DE∶BE,即3∶4=4∶BE.
解得BE=.
∴AB=AE+BE=.∴⊙O的半径为.
模型展示
1.如图,点A,B,C在⊙O上,BC=6,∠BAC=30°,则⊙O的半径为6.
2.如图,AB是⊙O的直径,弦CD垂直平分OB,P是上一点,则∠APD等于60°.
基础题
知识点1 半圆或直径所对的圆周角都相等,都等于90°(直角)
1.如图,BC是⊙O的直径,点A是⊙O上异于B,C的一点,则∠A的度数为( )
A.60° B.70° C.80° D.90°
2.如图,BC是⊙O的直径,A是⊙O上的一点,∠OAC=32°,则∠B的度数是( )
A.58° B.60° C.64° D.68°
3.如图,AB为⊙O的直径,点C,D在⊙O上,且BC=6 cm,AC=8 cm,∠ABD=45°.求BD的长.
知识点2 圆周角定理
4.如图,⊙O是△ABC的外接圆,∠BOC=120°,则∠BAC的度数是( )
A.120° B.80° C.60° D.30°
5.如图,在⊙O中,弦AB,CD相交于点P,∠A=42°,∠APD=77°,则∠B的大小是( )
A.43° B.35° C.34° D.44°
6.如图,在⊙O中,=,点D在⊙O上,∠CDB=25°,则∠AOB=( )
A.45° B.50° C.55° D.60°
7.如图,点A,B,C在⊙O上,AC∥OB,∠BAO=25°,则∠BOC的度数为( )
A.25° B.50° C.60° D.80°
8.同圆中,已知所对的圆心角是100°,则所对的圆周角是 .
9.如图,一块含45°角的直角三角板,它的一个锐角顶点A在⊙O上,边AB,AC分别与⊙O交于点D,E,则∠DOE的度数为 .
10.如图,AB为⊙O的直径,C,D为⊙O上的点,=.若∠CAB=40°,则∠CAD= .
11.如图,已知CD是⊙O的直径,弦AB⊥CD,垂足为M,点P是上一点,且∠BPC=60°.试判断△ABC的形状,并说明理由.
易错点 忽略弦所对的圆周角不唯一而致错
12.已知BC是半径为2 cm的圆内的一条弦,点A为圆上除点B,C外任意一点.若BC=2 cm,则∠BAC的度数为 .
中档题
13.如图,在⊙O中,AE是直径,半径OC垂直于弦AB于点D,连结BE.若AB=2,CD=1,则BE的长是( )
A.5 B.6
C.7 D.8
14.如图,⊙O是△ABC的外接圆,∠B=60°,OP⊥AC于点P,OP=4,则⊙O的半径为( )
A.8 B.12 C.8 D.12
15.如图,AB是⊙O的直径,且经过弦CD的中点H,已知sin∠CDB=,BD=5,则AH的长度为( )
A. B.
C. D.
16.如图,边长为1的小正方形网格中,⊙O的圆心在格点上,则∠AED的正弦值是 .
17.如图,AB是半圆O的直径,点C在半圆周上,连结AC,∠BAC=30°,点P在线段OB上运动.设∠ACP的度数是α,则α的取值范围为 .
18.如图,AB是⊙O的直径,CD是⊙O的一条弦,且CD⊥AB于点E.
(1)求证:∠BCO=∠D;
(2)若CD=8,AE=3,求⊙O的半径.
模型展示
1.如图,点A,B,C在⊙O上,BC=6,∠BAC=30°,则⊙O的半径为 .
2.如图,AB是⊙O的直径,弦CD垂直平分OB,P是上一点,则∠APD等于 .
2020春华师大版九下数学27.1.3圆周角第1课时圆周角定理同步课堂练习(学生版)
基础题
知识点1 半圆或直径所对的圆周角都相等,都等于90°(直角)
1.如图,BC是⊙O的直径,点A是⊙O上异于B,C的一点,则∠A的度数为(D)
A.60° B.70° C.80° D.90°
2.如图,BC是⊙O的直径,A是⊙O上的一点,∠OAC=32°,则∠B的度数是(A)
A.58° B.60° C.64° D.68°
3.如图,AB为⊙O的直径,点C,D在⊙O上,且BC=6 cm,AC=8 cm,∠ABD=45°.求BD的长.
解:连结OD.
∵AB为⊙O的直径,
∴∠ACB=90°.
∵BC=6 cm,AC=8 cm,
∴AB=10 cm.
∴OB=5 cm.
∵OD=OB,
∴∠ODB=∠ABD=45°.
∴∠BOD=90°.
∴BD==5 cm.
知识点2 圆周角定理
4.如图,⊙O是△ABC的外接圆,∠BOC=120°,则∠BAC的度数是(C)
A.120° B.80° C.60° D.30°
5.如图,在⊙O中,弦AB,CD相交于点P,∠A=42°,∠APD=77°,则∠B的大小是(B)
A.43° B.35° C.34° D.44°
6.如图,在⊙O中,=,点D在⊙O上,∠CDB=25°,则∠AOB=(B)
A.45° B.50° C.55° D.60°
7.如图,点A,B,C在⊙O上,AC∥OB,∠BAO=25°,则∠BOC的度数为(B)
A.25° B.50° C.60° D.80°
8.同圆中,已知所对的圆心角是100°,则所对的圆周角是50°.
9.如图,一块含45°角的直角三角板,它的一个锐角顶点A在⊙O上,边AB,AC分别与⊙O交于点D,E,则∠DOE的度数为90°.
10.如图,AB为⊙O的直径,C,D为⊙O上的点,=.若∠CAB=40°,则∠CAD=25°.
11.如图,已知CD是⊙O的直径,弦AB⊥CD,垂足为M,点P是上一点,且∠BPC=60°.试判断△ABC的形状,并说明理由.
解:△ABC为等边三角形.
理由:∵AB⊥CD,CD为⊙O的直径,
∴=.
∴AC=BC.
又∵∠BPC=∠A=60°,
∴△ABC为等边三角形.
易错点 忽略弦所对的圆周角不唯一而致错
12.已知BC是半径为2 cm的圆内的一条弦,点A为圆上除点B,C外任意一点.若BC=2 cm,则∠BAC的度数为60°或120°.
中档题
13.如图,在⊙O中,AE是直径,半径OC垂直于弦AB于点D,连结BE.若AB=2,CD=1,则BE的长是(B)
A.5 B.6
C.7 D.8
14.如图,⊙O是△ABC的外接圆,∠B=60°,OP⊥AC于点P,OP=4,则⊙O的半径为(C)
A.8 B.12 C.8 D.12
15.如图,AB是⊙O的直径,且经过弦CD的中点H,已知sin∠CDB=,BD=5,则AH的长度为(B)
A. B.
C. D.
16.如图,边长为1的小正方形网格中,⊙O的圆心在格点上,则∠AED的正弦值是.
17.如图,AB是半圆O的直径,点C在半圆周上,连结AC,∠BAC=30°,点P在线段OB上运动.设∠ACP的度数是α,则α的取值范围为30°≤α≤90°.
18.如图,AB是⊙O的直径,CD是⊙O的一条弦,且CD⊥AB于点E.
(1)求证:∠BCO=∠D;
(2)若CD=8,AE=3,求⊙O的半径.
解:(1)证明:∵OB=OC,
∴∠BCO=∠B.
∵∠B=∠D,
∴∠BCO=∠D.
(2)∵AB是⊙O的直径,CD⊥AB,
∴CE=DE=CD=×8=4.
∵∠B=∠D,∠BEC=∠DEA,
∴△BCE∽△DAE.
∴AE∶CE=DE∶BE,即3∶4=4∶BE.
解得BE=.
∴AB=AE+BE=.∴⊙O的半径为.
模型展示
1.如图,点A,B,C在⊙O上,BC=6,∠BAC=30°,则⊙O的半径为6.
2.如图,AB是⊙O的直径,弦CD垂直平分OB,P是上一点,则∠APD等于60°.
