2020春华师大版九下数学27.2.1点与圆的位置关系同步课堂练习含答案
文档属性
| 名称 | 2020春华师大版九下数学27.2.1点与圆的位置关系同步课堂练习含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 146.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-20 13:35:47 | ||
图片预览


文档简介
2020春华师大版九下数学27.2.1点与圆的位置关系同步课堂练习(学生版)
基础题
知识点1 点与圆的位置关系
1.若⊙O的半径为5 cm,点A到圆心O的距离为4 cm,则点A与⊙O的位置关系是( )
A.点A在圆外 B.点A在圆上
C.点A在圆内 D.不能确定
2.若⊙P的半径为13,圆心P的坐标为(5,12),则平面直角坐标系的原点O与⊙P的位置关系是( )
A.在⊙P内 B.在⊙P上
C.在⊙P外 D.无法确定
3.已知⊙O的半径为7 cm,点A为线段OP的中点,当OP满足下列条件时,分别指出点A与⊙O的位置关系.
(1)OP=8 cm;(2)OP=14 cm;(3)OP=16 cm.
知识点2 过不在同一直线上的三点作圆
4.下列条件,可以画出圆的是( )
A.已知圆心
B.已知半径
C.已知不在同一直线上的三点
D.已知直径
5.如图,在5×5的正方形网格中,一条圆弧经过A,B,C三点,那么这条圆弧所在的圆心是( )
A.点P B.点Q C.点R D.点M
6.如图,点A,B,C在同一条直线上,点D在直线AB外,过这四点中的任意3个点,能画圆的个数是( )
A.1个 B.2个 C.3个 D.4个
7.经过A,B两点的圆有 个,圆心在 .
知识点3 三角形的外接圆
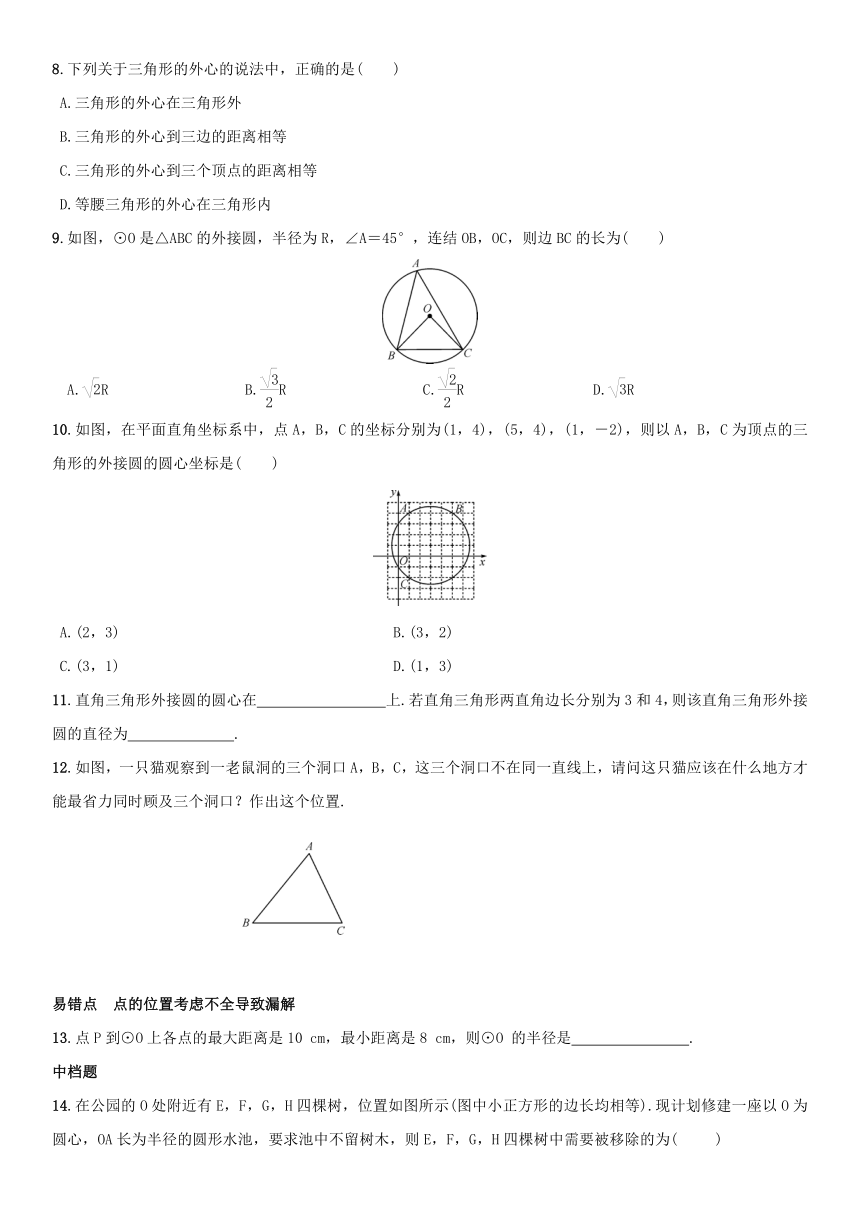
8.下列关于三角形的外心的说法中,正确的是( )
A.三角形的外心在三角形外
B.三角形的外心到三边的距离相等
C.三角形的外心到三个顶点的距离相等
D.等腰三角形的外心在三角形内
9.如图,⊙O是△ABC的外接圆,半径为R,∠A=45°,连结OB,OC,则边BC的长为( )
A.R B.R C.R D.R
10.如图,在平面直角坐标系中,点A,B,C的坐标分别为(1,4),(5,4),(1,-2),则以A,B,C为顶点的三角形的外接圆的圆心坐标是( )
A.(2,3) B.(3,2)
C.(3,1) D.(1,3)
11.直角三角形外接圆的圆心在 上.若直角三角形两直角边长分别为3和4,则该直角三角形外接圆的直径为 .
12.如图,一只猫观察到一老鼠洞的三个洞口A,B,C,这三个洞口不在同一直线上,请问这只猫应该在什么地方才能最省力同时顾及三个洞口?作出这个位置.
易错点 点的位置考虑不全导致漏解
13.点P到⊙O上各点的最大距离是10 cm,最小距离是8 cm,则⊙O 的半径是 .
中档题
14.在公园的O处附近有E,F,G,H四棵树,位置如图所示(图中小正方形的边长均相等).现计划修建一座以O为圆心,OA长为半径的圆形水池,要求池中不留树木,则E,F,G,H四棵树中需要被移除的为( )
A.E,F,G
B.F,G,H
C.G,H,E
D.H,E,F
15.小明不慎把家里的圆形镜子打碎了,其中四块碎片如图所示,为了配到与原来大小一样的圆形镜子,小明带到商店去的一块碎片应该是( )
A.① B.② C.③ D.④
16.如图,在△ABC中,∠A=60°,BC=5 cm.能够将△ABC完全覆盖的最小圆形纸片的直径是 cm.
17.小明家的房前有一块矩形的空地,空地上有三棵树A,B,C,小明想建一个圆形花坛,使三棵树都在花坛的边上.
(1)请你帮小明把花坛的位置画出来(尺规作图,不写作法,保留作图痕迹);
(2)若在△ABC中,AB=8米,AC=6米,∠BAC=90°,试求小明家圆形花坛的面积.
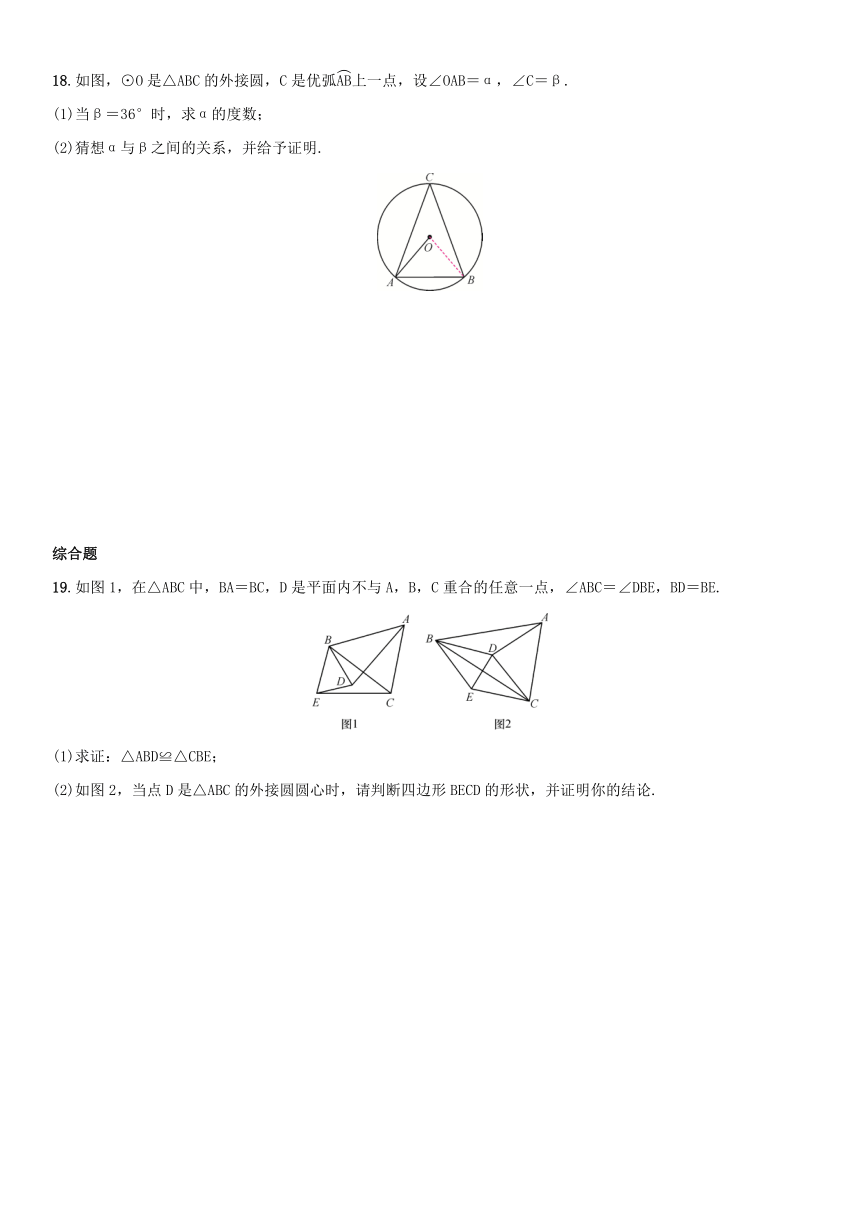
18.如图,⊙O是△ABC的外接圆,C是优弧上一点,设∠OAB=α,∠C=β.
(1)当β=36°时,求α的度数;
(2)猜想α与β之间的关系,并给予证明.
综合题
19.如图1,在△ABC中,BA=BC,D是平面内不与A,B,C重合的任意一点,∠ABC=∠DBE,BD=BE.
(1)求证:△ABD≌△CBE;
(2)如图2,当点D是△ABC的外接圆圆心时,请判断四边形BECD的形状,并证明你的结论.
2020春华师大版九下数学27.2.1点与圆的位置关系同步课堂练习(教师版)
基础题
知识点1 点与圆的位置关系
1.若⊙O的半径为5 cm,点A到圆心O的距离为4 cm,则点A与⊙O的位置关系是(C)
A.点A在圆外 B.点A在圆上
C.点A在圆内 D.不能确定
2.若⊙P的半径为13,圆心P的坐标为(5,12),则平面直角坐标系的原点O与⊙P的位置关系是(B)
A.在⊙P内 B.在⊙P上
C.在⊙P外 D.无法确定
3.已知⊙O的半径为7 cm,点A为线段OP的中点,当OP满足下列条件时,分别指出点A与⊙O的位置关系.
(1)OP=8 cm;(2)OP=14 cm;(3)OP=16 cm.
解:(1)在圆内;(2)在圆上;(3)在圆外.
知识点2 过不在同一直线上的三点作圆
4.下列条件,可以画出圆的是(C)
A.已知圆心
B.已知半径
C.已知不在同一直线上的三点
D.已知直径
5.如图,在5×5的正方形网格中,一条圆弧经过A,B,C三点,那么这条圆弧所在的圆心是(B)
A.点P B.点Q C.点R D.点M
6.如图,点A,B,C在同一条直线上,点D在直线AB外,过这四点中的任意3个点,能画圆的个数是(C)
A.1个 B.2个 C.3个 D.4个
7.经过A,B两点的圆有无数个,圆心在线段AB的垂直平分线上.
知识点3 三角形的外接圆
8.下列关于三角形的外心的说法中,正确的是(C)
A.三角形的外心在三角形外
B.三角形的外心到三边的距离相等
C.三角形的外心到三个顶点的距离相等
D.等腰三角形的外心在三角形内
9.如图,⊙O是△ABC的外接圆,半径为R,∠A=45°,连结OB,OC,则边BC的长为(A)
A.R B.R C.R D.R
10.如图,在平面直角坐标系中,点A,B,C的坐标分别为(1,4),(5,4),(1,-2),则以A,B,C为顶点的三角形的外接圆的圆心坐标是(C)
A.(2,3) B.(3,2)
C.(3,1) D.(1,3)
11.直角三角形外接圆的圆心在斜边的中点上.若直角三角形两直角边长分别为3和4,则该直角三角形外接圆的直径为5.
12.如图,一只猫观察到一老鼠洞的三个洞口A,B,C,这三个洞口不在同一直线上,请问这只猫应该在什么地方才能最省力同时顾及三个洞口?作出这个位置.
解:如图,连结AB,BC,分别作线段AB,BC的垂直平分线,且相交于点O,点O即为所求.
易错点 点的位置考虑不全导致漏解
13.点P到⊙O上各点的最大距离是10 cm,最小距离是8 cm,则⊙O 的半径是1或9cm.
中档题
14.在公园的O处附近有E,F,G,H四棵树,位置如图所示(图中小正方形的边长均相等).现计划修建一座以O为圆心,OA长为半径的圆形水池,要求池中不留树木,则E,F,G,H四棵树中需要被移除的为(A)
A.E,F,G
B.F,G,H
C.G,H,E
D.H,E,F
15.小明不慎把家里的圆形镜子打碎了,其中四块碎片如图所示,为了配到与原来大小一样的圆形镜子,小明带到商店去的一块碎片应该是(A)
A.① B.② C.③ D.④
16.如图,在△ABC中,∠A=60°,BC=5 cm.能够将△ABC完全覆盖的最小圆形纸片的直径是cm.
17.小明家的房前有一块矩形的空地,空地上有三棵树A,B,C,小明想建一个圆形花坛,使三棵树都在花坛的边上.
(1)请你帮小明把花坛的位置画出来(尺规作图,不写作法,保留作图痕迹);
(2)若在△ABC中,AB=8米,AC=6米,∠BAC=90°,试求小明家圆形花坛的面积.
解:(1)用尺规作出△ABC中任意两边的垂直平分线,交于O点,以O为圆心,OA长为半径作出⊙O,⊙O即为所求作的花坛的位置.图略.
(2)∵∠BAC=90°,AB=8米,AC=6米,
∴在Rt△ABC中,由勾股定理,得BC=10米.
∴△ABC外接圆的半径为5米.
∴小明家圆形花坛的面积为25π平方米.
18.如图,⊙O是△ABC的外接圆,C是优弧上一点,设∠OAB=α,∠C=β.
(1)当β=36°时,求α的度数;
(2)猜想α与β之间的关系,并给予证明.
解:(1)连结OB,则OA=OB,
∴∠OAB=∠OBA.
∵∠C=36°,
∴∠AOB=72°.
∴∠OAB=×(180°-∠AOB)=54°,即α=54°.
(2)α与β之间的关系是α+β=90°.
证明:∵∠OBA=∠OAB=α,
∴∠AOB=180°-2α.
∵∠AOB=2β,
∴180°-2α=2β.
∴α+β=90°.
综合题
19.如图1,在△ABC中,BA=BC,D是平面内不与A,B,C重合的任意一点,∠ABC=∠DBE,BD=BE.
(1)求证:△ABD≌△CBE;
(2)如图2,当点D是△ABC的外接圆圆心时,请判断四边形BECD的形状,并证明你的结论.
解:(1)证明:∵∠ABC=∠DBE,
∴∠ABD=∠CBE.
又∵BA=BC,BD=BE,
∴△ABD≌△CBE(SAS).
(2)四边形BECD是菱形.
证明:∵△ABD≌△CBE,∴AD=CE.
∵点D是△ABC的外接圆圆心,
∴AD=BD=CD.
又∵BD=BE,∴BD=BE=EC=CD.
∴四边形BECD是菱形.
基础题
知识点1 点与圆的位置关系
1.若⊙O的半径为5 cm,点A到圆心O的距离为4 cm,则点A与⊙O的位置关系是( )
A.点A在圆外 B.点A在圆上
C.点A在圆内 D.不能确定
2.若⊙P的半径为13,圆心P的坐标为(5,12),则平面直角坐标系的原点O与⊙P的位置关系是( )
A.在⊙P内 B.在⊙P上
C.在⊙P外 D.无法确定
3.已知⊙O的半径为7 cm,点A为线段OP的中点,当OP满足下列条件时,分别指出点A与⊙O的位置关系.
(1)OP=8 cm;(2)OP=14 cm;(3)OP=16 cm.
知识点2 过不在同一直线上的三点作圆
4.下列条件,可以画出圆的是( )
A.已知圆心
B.已知半径
C.已知不在同一直线上的三点
D.已知直径
5.如图,在5×5的正方形网格中,一条圆弧经过A,B,C三点,那么这条圆弧所在的圆心是( )
A.点P B.点Q C.点R D.点M
6.如图,点A,B,C在同一条直线上,点D在直线AB外,过这四点中的任意3个点,能画圆的个数是( )
A.1个 B.2个 C.3个 D.4个
7.经过A,B两点的圆有 个,圆心在 .
知识点3 三角形的外接圆
8.下列关于三角形的外心的说法中,正确的是( )
A.三角形的外心在三角形外
B.三角形的外心到三边的距离相等
C.三角形的外心到三个顶点的距离相等
D.等腰三角形的外心在三角形内
9.如图,⊙O是△ABC的外接圆,半径为R,∠A=45°,连结OB,OC,则边BC的长为( )
A.R B.R C.R D.R
10.如图,在平面直角坐标系中,点A,B,C的坐标分别为(1,4),(5,4),(1,-2),则以A,B,C为顶点的三角形的外接圆的圆心坐标是( )
A.(2,3) B.(3,2)
C.(3,1) D.(1,3)
11.直角三角形外接圆的圆心在 上.若直角三角形两直角边长分别为3和4,则该直角三角形外接圆的直径为 .
12.如图,一只猫观察到一老鼠洞的三个洞口A,B,C,这三个洞口不在同一直线上,请问这只猫应该在什么地方才能最省力同时顾及三个洞口?作出这个位置.
易错点 点的位置考虑不全导致漏解
13.点P到⊙O上各点的最大距离是10 cm,最小距离是8 cm,则⊙O 的半径是 .
中档题
14.在公园的O处附近有E,F,G,H四棵树,位置如图所示(图中小正方形的边长均相等).现计划修建一座以O为圆心,OA长为半径的圆形水池,要求池中不留树木,则E,F,G,H四棵树中需要被移除的为( )
A.E,F,G
B.F,G,H
C.G,H,E
D.H,E,F
15.小明不慎把家里的圆形镜子打碎了,其中四块碎片如图所示,为了配到与原来大小一样的圆形镜子,小明带到商店去的一块碎片应该是( )
A.① B.② C.③ D.④
16.如图,在△ABC中,∠A=60°,BC=5 cm.能够将△ABC完全覆盖的最小圆形纸片的直径是 cm.
17.小明家的房前有一块矩形的空地,空地上有三棵树A,B,C,小明想建一个圆形花坛,使三棵树都在花坛的边上.
(1)请你帮小明把花坛的位置画出来(尺规作图,不写作法,保留作图痕迹);
(2)若在△ABC中,AB=8米,AC=6米,∠BAC=90°,试求小明家圆形花坛的面积.
18.如图,⊙O是△ABC的外接圆,C是优弧上一点,设∠OAB=α,∠C=β.
(1)当β=36°时,求α的度数;
(2)猜想α与β之间的关系,并给予证明.
综合题
19.如图1,在△ABC中,BA=BC,D是平面内不与A,B,C重合的任意一点,∠ABC=∠DBE,BD=BE.
(1)求证:△ABD≌△CBE;
(2)如图2,当点D是△ABC的外接圆圆心时,请判断四边形BECD的形状,并证明你的结论.
2020春华师大版九下数学27.2.1点与圆的位置关系同步课堂练习(教师版)
基础题
知识点1 点与圆的位置关系
1.若⊙O的半径为5 cm,点A到圆心O的距离为4 cm,则点A与⊙O的位置关系是(C)
A.点A在圆外 B.点A在圆上
C.点A在圆内 D.不能确定
2.若⊙P的半径为13,圆心P的坐标为(5,12),则平面直角坐标系的原点O与⊙P的位置关系是(B)
A.在⊙P内 B.在⊙P上
C.在⊙P外 D.无法确定
3.已知⊙O的半径为7 cm,点A为线段OP的中点,当OP满足下列条件时,分别指出点A与⊙O的位置关系.
(1)OP=8 cm;(2)OP=14 cm;(3)OP=16 cm.
解:(1)在圆内;(2)在圆上;(3)在圆外.
知识点2 过不在同一直线上的三点作圆
4.下列条件,可以画出圆的是(C)
A.已知圆心
B.已知半径
C.已知不在同一直线上的三点
D.已知直径
5.如图,在5×5的正方形网格中,一条圆弧经过A,B,C三点,那么这条圆弧所在的圆心是(B)
A.点P B.点Q C.点R D.点M
6.如图,点A,B,C在同一条直线上,点D在直线AB外,过这四点中的任意3个点,能画圆的个数是(C)
A.1个 B.2个 C.3个 D.4个
7.经过A,B两点的圆有无数个,圆心在线段AB的垂直平分线上.
知识点3 三角形的外接圆
8.下列关于三角形的外心的说法中,正确的是(C)
A.三角形的外心在三角形外
B.三角形的外心到三边的距离相等
C.三角形的外心到三个顶点的距离相等
D.等腰三角形的外心在三角形内
9.如图,⊙O是△ABC的外接圆,半径为R,∠A=45°,连结OB,OC,则边BC的长为(A)
A.R B.R C.R D.R
10.如图,在平面直角坐标系中,点A,B,C的坐标分别为(1,4),(5,4),(1,-2),则以A,B,C为顶点的三角形的外接圆的圆心坐标是(C)
A.(2,3) B.(3,2)
C.(3,1) D.(1,3)
11.直角三角形外接圆的圆心在斜边的中点上.若直角三角形两直角边长分别为3和4,则该直角三角形外接圆的直径为5.
12.如图,一只猫观察到一老鼠洞的三个洞口A,B,C,这三个洞口不在同一直线上,请问这只猫应该在什么地方才能最省力同时顾及三个洞口?作出这个位置.
解:如图,连结AB,BC,分别作线段AB,BC的垂直平分线,且相交于点O,点O即为所求.
易错点 点的位置考虑不全导致漏解
13.点P到⊙O上各点的最大距离是10 cm,最小距离是8 cm,则⊙O 的半径是1或9cm.
中档题
14.在公园的O处附近有E,F,G,H四棵树,位置如图所示(图中小正方形的边长均相等).现计划修建一座以O为圆心,OA长为半径的圆形水池,要求池中不留树木,则E,F,G,H四棵树中需要被移除的为(A)
A.E,F,G
B.F,G,H
C.G,H,E
D.H,E,F
15.小明不慎把家里的圆形镜子打碎了,其中四块碎片如图所示,为了配到与原来大小一样的圆形镜子,小明带到商店去的一块碎片应该是(A)
A.① B.② C.③ D.④
16.如图,在△ABC中,∠A=60°,BC=5 cm.能够将△ABC完全覆盖的最小圆形纸片的直径是cm.
17.小明家的房前有一块矩形的空地,空地上有三棵树A,B,C,小明想建一个圆形花坛,使三棵树都在花坛的边上.
(1)请你帮小明把花坛的位置画出来(尺规作图,不写作法,保留作图痕迹);
(2)若在△ABC中,AB=8米,AC=6米,∠BAC=90°,试求小明家圆形花坛的面积.
解:(1)用尺规作出△ABC中任意两边的垂直平分线,交于O点,以O为圆心,OA长为半径作出⊙O,⊙O即为所求作的花坛的位置.图略.
(2)∵∠BAC=90°,AB=8米,AC=6米,
∴在Rt△ABC中,由勾股定理,得BC=10米.
∴△ABC外接圆的半径为5米.
∴小明家圆形花坛的面积为25π平方米.
18.如图,⊙O是△ABC的外接圆,C是优弧上一点,设∠OAB=α,∠C=β.
(1)当β=36°时,求α的度数;
(2)猜想α与β之间的关系,并给予证明.
解:(1)连结OB,则OA=OB,
∴∠OAB=∠OBA.
∵∠C=36°,
∴∠AOB=72°.
∴∠OAB=×(180°-∠AOB)=54°,即α=54°.
(2)α与β之间的关系是α+β=90°.
证明:∵∠OBA=∠OAB=α,
∴∠AOB=180°-2α.
∵∠AOB=2β,
∴180°-2α=2β.
∴α+β=90°.
综合题
19.如图1,在△ABC中,BA=BC,D是平面内不与A,B,C重合的任意一点,∠ABC=∠DBE,BD=BE.
(1)求证:△ABD≌△CBE;
(2)如图2,当点D是△ABC的外接圆圆心时,请判断四边形BECD的形状,并证明你的结论.
解:(1)证明:∵∠ABC=∠DBE,
∴∠ABD=∠CBE.
又∵BA=BC,BD=BE,
∴△ABD≌△CBE(SAS).
(2)四边形BECD是菱形.
证明:∵△ABD≌△CBE,∴AD=CE.
∵点D是△ABC的外接圆圆心,
∴AD=BD=CD.
又∵BD=BE,∴BD=BE=EC=CD.
∴四边形BECD是菱形.
