2020春华师大版九下数学27.2.3切线第2课时切线长定理和三角形的内切圆同步课堂练习含答案
文档属性
| 名称 | 2020春华师大版九下数学27.2.3切线第2课时切线长定理和三角形的内切圆同步课堂练习含答案 |
|
|
| 格式 | zip | ||
| 文件大小 | 211.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-20 00:00:00 | ||
图片预览



文档简介
2020春华师大版九下数学27.2.3切线第2课时切线长定理和三角形的内切圆同步课堂练习(学生版)
基础题
知识点1 切线长定理
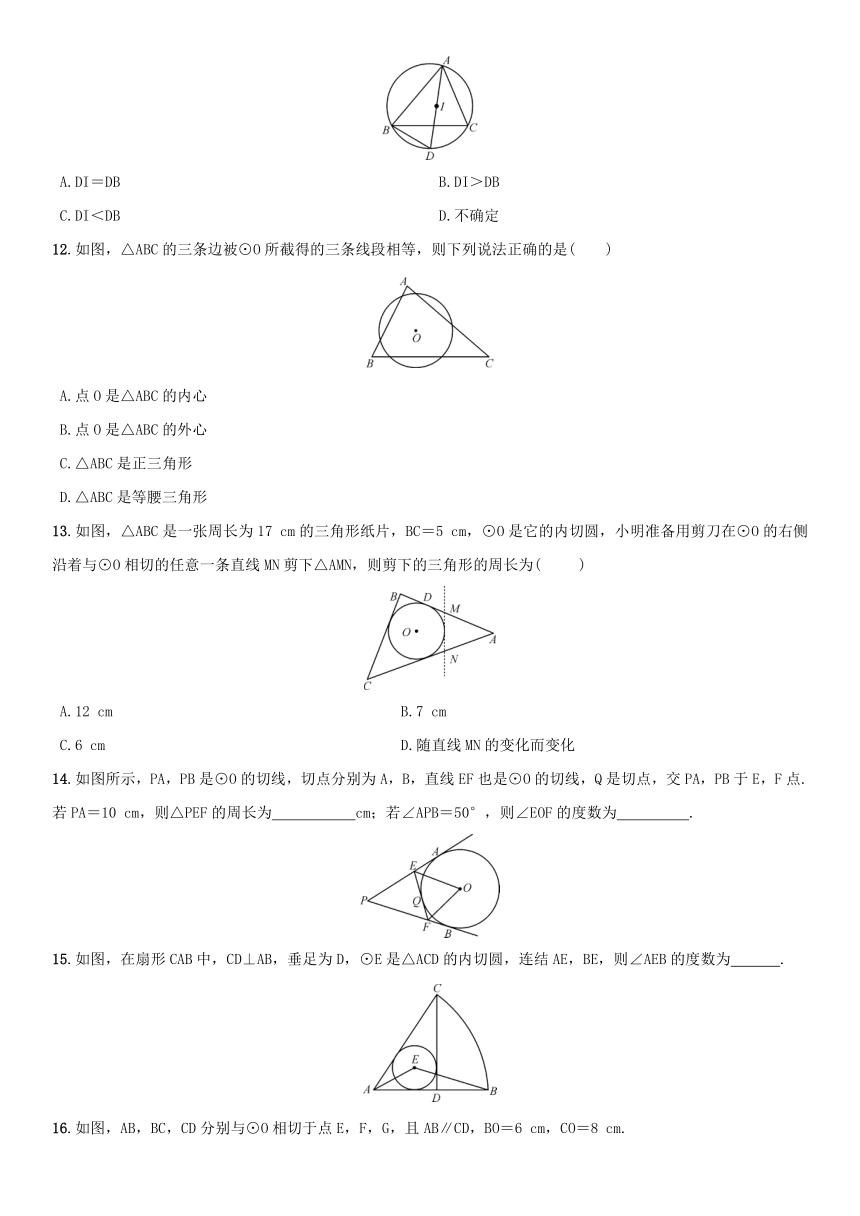
1.如图,P为⊙O外一点,PA,PB分别切⊙O于A,B两点.若PA=3,则PB=( )
A.2 B.3 C.4 D.5
2.如图,PA,PB是⊙O的两条切线,切点分别是A,B.如果OP=4,PA=2,那么∠APB等于( )
A.45° B.60° C.75° D.90°
3.如图,已知以直角梯形ABCD的腰CD为直径的半圆O与梯形上底AD,下底BC以及腰AB均相切,切点分别是D,C,E.若半圆O的半径为2,梯形的腰AB为5,则该梯形的周长是( )
A.9 B.10 C.12 D.14
4.如图,AB,AC,BD是⊙O的切线,P,C,D为切点.若AB=5,AC=3,则BD的长为 .
5.为了测量一个圆形铁环的半径,某同学采用了如下办法:将铁环平放在水平桌面上,用一个锐角为30°的三角板和一个刻度尺,按如图所示的方法得到相关数据,进而可求得铁环的半径.若三角板与圆相切且测得PA=5 cm,求铁环的半径.
知识点2 三角形的内切圆
6.如图,⊙O是△ABC的内切圆,则点O是△ABC的( )
A.三条边的垂直平分线的交点
B.三条角平分线的交点
C.三条中线的交点
D.三条高的交点
7.如图,△ABC的内切圆的三个切点分别为D,E,F,∠A=75°,∠B=45°,则圆心角∠EOF= 度.
8.《九章算术》是东方数学思想之源,该书中记载:“今有勾八步,股一十五步,问勾中容圆径几何?”其意思为:“今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形内切圆的直径是多少步?”该问题的答案是 步.
9.如图,△ABC的内切圆⊙O与BC,CA,AB分别相切于点D,E,F,且AB=18 cm,BC=28 cm,CA=26 cm,求AF,BD,CE的长.
易错点 内心与外心概念混淆不清
10.如图,△ABC是圆的内接三角形,点P是△ABC的内心,∠A=50°,则∠BPC的度数是 .
中档题
11.如图,△ABC的内心为I,连结AI并延长交△ABC的外接圆于D,则线段DI与DB的关系是( )
A.DI=DB B.DI>DB
C.DI<DB D.不确定
12.如图,△ABC的三条边被⊙O所截得的三条线段相等,则下列说法正确的是( )
A.点O是△ABC的内心
B.点O是△ABC的外心
C.△ABC是正三角形
D.△ABC是等腰三角形
13.如图,△ABC是一张周长为17 cm的三角形纸片,BC=5 cm,⊙O是它的内切圆,小明准备用剪刀在⊙O的右侧沿着与⊙O相切的任意一条直线MN剪下△AMN,则剪下的三角形的周长为( )
A.12 cm B.7 cm
C.6 cm D.随直线MN的变化而变化
14.如图所示,PA,PB是⊙O的切线,切点分别为A,B,直线EF也是⊙O的切线,Q是切点,交PA,PB于E,F点.若PA=10 cm,则△PEF的周长为 cm;若∠APB=50°,则∠EOF的度数为 .
15.如图,在扇形CAB中,CD⊥AB,垂足为D,⊙E是△ACD的内切圆,连结AE,BE,则∠AEB的度数为 .
16.如图,AB,BC,CD分别与⊙O相切于点E,F,G,且AB∥CD,BO=6 cm,CO=8 cm.
(1)求证:BO⊥CO;
(2)求BE和CG的长.
综合题
17.如图,PA,PB切⊙O于A,B两点,CD切⊙O于点E,交PA,PB于点C,D.若⊙O的半径为r,△PCD的周长等于3r,则tan∠APB的值是( )
A. B.
C. D.
2020春华师大版九下数学27.2.3切线第2课时切线长定理和三角形的内切圆同步课堂练习(教师版)
基础题
知识点1 切线长定理
1.如图,P为⊙O外一点,PA,PB分别切⊙O于A,B两点.若PA=3,则PB=(B)
A.2 B.3 C.4 D.5
2.如图,PA,PB是⊙O的两条切线,切点分别是A,B.如果OP=4,PA=2,那么∠APB等于(B)
A.45° B.60° C.75° D.90°
3.如图,已知以直角梯形ABCD的腰CD为直径的半圆O与梯形上底AD,下底BC以及腰AB均相切,切点分别是D,C,E.若半圆O的半径为2,梯形的腰AB为5,则该梯形的周长是(D)
A.9 B.10 C.12 D.14
4.如图,AB,AC,BD是⊙O的切线,P,C,D为切点.若AB=5,AC=3,则BD的长为2.
5.为了测量一个圆形铁环的半径,某同学采用了如下办法:将铁环平放在水平桌面上,用一个锐角为30°的三角板和一个刻度尺,按如图所示的方法得到相关数据,进而可求得铁环的半径.若三角板与圆相切且测得PA=5 cm,求铁环的半径.
解:设圆心为O,连结OA,OP.
∵三角板有一个锐角为30°,
∴∠PAO=60°.
又∵PA与⊙O相切,
∴∠OPA=90°.
∴∠POA=30°.
∵PA=5 cm,
∴OA=10 cm,OP=5 cm.
∴铁环的半径为5 cm.
知识点2 三角形的内切圆
6.如图,⊙O是△ABC的内切圆,则点O是△ABC的(B)
A.三条边的垂直平分线的交点
B.三条角平分线的交点
C.三条中线的交点
D.三条高的交点
7.如图,△ABC的内切圆的三个切点分别为D,E,F,∠A=75°,∠B=45°,则圆心角∠EOF=120度.
8.《九章算术》是东方数学思想之源,该书中记载:“今有勾八步,股一十五步,问勾中容圆径几何?”其意思为:“今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形内切圆的直径是多少步?”该问题的答案是6步.
9.如图,△ABC的内切圆⊙O与BC,CA,AB分别相切于点D,E,F,且AB=18 cm,BC=28 cm,CA=26 cm,求AF,BD,CE的长.
解:根据切线长定理,得
AE=AF,BF=BD,CE=CD.
设AF=AE=x cm,
则CE=CD=(26-x)cm,
BF=BD=(18-x)cm.
∵BC=28 cm,
∴(18-x)+(26-x)=28.解得x=8.
∴AF=8 cm,BD=10 cm,CE=18 cm.
易错点 内心与外心概念混淆不清
10.如图,△ABC是圆的内接三角形,点P是△ABC的内心,∠A=50°,则∠BPC的度数是115°.
中档题
11.如图,△ABC的内心为I,连结AI并延长交△ABC的外接圆于D,则线段DI与DB的关系是(A)
A.DI=DB B.DI>DB
C.DI<DB D.不确定
12.如图,△ABC的三条边被⊙O所截得的三条线段相等,则下列说法正确的是(A)
A.点O是△ABC的内心
B.点O是△ABC的外心
C.△ABC是正三角形
D.△ABC是等腰三角形
13.如图,△ABC是一张周长为17 cm的三角形纸片,BC=5 cm,⊙O是它的内切圆,小明准备用剪刀在⊙O的右侧沿着与⊙O相切的任意一条直线MN剪下△AMN,则剪下的三角形的周长为(B)
A.12 cm B.7 cm
C.6 cm D.随直线MN的变化而变化
14.如图所示,PA,PB是⊙O的切线,切点分别为A,B,直线EF也是⊙O的切线,Q是切点,交PA,PB于E,F点.若PA=10 cm,则△PEF的周长为20cm;若∠APB=50°,则∠EOF的度数为65°.
15.如图,在扇形CAB中,CD⊥AB,垂足为D,⊙E是△ACD的内切圆,连结AE,BE,则∠AEB的度数为135°.
16.如图,AB,BC,CD分别与⊙O相切于点E,F,G,且AB∥CD,BO=6 cm,CO=8 cm.
(1)求证:BO⊥CO;(2)求BE和CG的长.
解:(1)证明:∵AB∥CD,
∴∠ABC+∠DCB=180°.
∵AB,BC,CD分别与⊙O相切于点E,F,G,
∴BO平分∠ABC,CO平分∠DCB.
∴∠OBC=∠ABC,∠OCB=∠DCB.
∴∠OBC+∠OCB=(∠ABC+∠DCB)
=×180°=90°.
∴∠BOC=90°.∴BO⊥CO.
(2)连结OF,则OF⊥BC,
∴Rt△BOF∽Rt△BCO.∴=.
∵在Rt△BOC中,BO=6 cm,CO=8 cm,
∴BC==10(cm).
∴=.∴BF=3.6 cm.
∵AB,BC,CD分别与⊙O相切,
∴BE=BF=3.6 cm,CG=CF.
∵CF=BC-BF=10-3.6=6.4(cm),
∴CG=CF=6.4 cm.
综合题
17.如图,PA,PB切⊙O于A,B两点,CD切⊙O于点E,交PA,PB于点C,D.若⊙O的半径为r,△PCD的周长等于3r,则tan∠APB的值是(B)
A. B.
C. D.
基础题
知识点1 切线长定理
1.如图,P为⊙O外一点,PA,PB分别切⊙O于A,B两点.若PA=3,则PB=( )
A.2 B.3 C.4 D.5
2.如图,PA,PB是⊙O的两条切线,切点分别是A,B.如果OP=4,PA=2,那么∠APB等于( )
A.45° B.60° C.75° D.90°
3.如图,已知以直角梯形ABCD的腰CD为直径的半圆O与梯形上底AD,下底BC以及腰AB均相切,切点分别是D,C,E.若半圆O的半径为2,梯形的腰AB为5,则该梯形的周长是( )
A.9 B.10 C.12 D.14
4.如图,AB,AC,BD是⊙O的切线,P,C,D为切点.若AB=5,AC=3,则BD的长为 .
5.为了测量一个圆形铁环的半径,某同学采用了如下办法:将铁环平放在水平桌面上,用一个锐角为30°的三角板和一个刻度尺,按如图所示的方法得到相关数据,进而可求得铁环的半径.若三角板与圆相切且测得PA=5 cm,求铁环的半径.
知识点2 三角形的内切圆
6.如图,⊙O是△ABC的内切圆,则点O是△ABC的( )
A.三条边的垂直平分线的交点
B.三条角平分线的交点
C.三条中线的交点
D.三条高的交点
7.如图,△ABC的内切圆的三个切点分别为D,E,F,∠A=75°,∠B=45°,则圆心角∠EOF= 度.
8.《九章算术》是东方数学思想之源,该书中记载:“今有勾八步,股一十五步,问勾中容圆径几何?”其意思为:“今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形内切圆的直径是多少步?”该问题的答案是 步.
9.如图,△ABC的内切圆⊙O与BC,CA,AB分别相切于点D,E,F,且AB=18 cm,BC=28 cm,CA=26 cm,求AF,BD,CE的长.
易错点 内心与外心概念混淆不清
10.如图,△ABC是圆的内接三角形,点P是△ABC的内心,∠A=50°,则∠BPC的度数是 .
中档题
11.如图,△ABC的内心为I,连结AI并延长交△ABC的外接圆于D,则线段DI与DB的关系是( )
A.DI=DB B.DI>DB
C.DI<DB D.不确定
12.如图,△ABC的三条边被⊙O所截得的三条线段相等,则下列说法正确的是( )
A.点O是△ABC的内心
B.点O是△ABC的外心
C.△ABC是正三角形
D.△ABC是等腰三角形
13.如图,△ABC是一张周长为17 cm的三角形纸片,BC=5 cm,⊙O是它的内切圆,小明准备用剪刀在⊙O的右侧沿着与⊙O相切的任意一条直线MN剪下△AMN,则剪下的三角形的周长为( )
A.12 cm B.7 cm
C.6 cm D.随直线MN的变化而变化
14.如图所示,PA,PB是⊙O的切线,切点分别为A,B,直线EF也是⊙O的切线,Q是切点,交PA,PB于E,F点.若PA=10 cm,则△PEF的周长为 cm;若∠APB=50°,则∠EOF的度数为 .
15.如图,在扇形CAB中,CD⊥AB,垂足为D,⊙E是△ACD的内切圆,连结AE,BE,则∠AEB的度数为 .
16.如图,AB,BC,CD分别与⊙O相切于点E,F,G,且AB∥CD,BO=6 cm,CO=8 cm.
(1)求证:BO⊥CO;
(2)求BE和CG的长.
综合题
17.如图,PA,PB切⊙O于A,B两点,CD切⊙O于点E,交PA,PB于点C,D.若⊙O的半径为r,△PCD的周长等于3r,则tan∠APB的值是( )
A. B.
C. D.
2020春华师大版九下数学27.2.3切线第2课时切线长定理和三角形的内切圆同步课堂练习(教师版)
基础题
知识点1 切线长定理
1.如图,P为⊙O外一点,PA,PB分别切⊙O于A,B两点.若PA=3,则PB=(B)
A.2 B.3 C.4 D.5
2.如图,PA,PB是⊙O的两条切线,切点分别是A,B.如果OP=4,PA=2,那么∠APB等于(B)
A.45° B.60° C.75° D.90°
3.如图,已知以直角梯形ABCD的腰CD为直径的半圆O与梯形上底AD,下底BC以及腰AB均相切,切点分别是D,C,E.若半圆O的半径为2,梯形的腰AB为5,则该梯形的周长是(D)
A.9 B.10 C.12 D.14
4.如图,AB,AC,BD是⊙O的切线,P,C,D为切点.若AB=5,AC=3,则BD的长为2.
5.为了测量一个圆形铁环的半径,某同学采用了如下办法:将铁环平放在水平桌面上,用一个锐角为30°的三角板和一个刻度尺,按如图所示的方法得到相关数据,进而可求得铁环的半径.若三角板与圆相切且测得PA=5 cm,求铁环的半径.
解:设圆心为O,连结OA,OP.
∵三角板有一个锐角为30°,
∴∠PAO=60°.
又∵PA与⊙O相切,
∴∠OPA=90°.
∴∠POA=30°.
∵PA=5 cm,
∴OA=10 cm,OP=5 cm.
∴铁环的半径为5 cm.
知识点2 三角形的内切圆
6.如图,⊙O是△ABC的内切圆,则点O是△ABC的(B)
A.三条边的垂直平分线的交点
B.三条角平分线的交点
C.三条中线的交点
D.三条高的交点
7.如图,△ABC的内切圆的三个切点分别为D,E,F,∠A=75°,∠B=45°,则圆心角∠EOF=120度.
8.《九章算术》是东方数学思想之源,该书中记载:“今有勾八步,股一十五步,问勾中容圆径几何?”其意思为:“今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形内切圆的直径是多少步?”该问题的答案是6步.
9.如图,△ABC的内切圆⊙O与BC,CA,AB分别相切于点D,E,F,且AB=18 cm,BC=28 cm,CA=26 cm,求AF,BD,CE的长.
解:根据切线长定理,得
AE=AF,BF=BD,CE=CD.
设AF=AE=x cm,
则CE=CD=(26-x)cm,
BF=BD=(18-x)cm.
∵BC=28 cm,
∴(18-x)+(26-x)=28.解得x=8.
∴AF=8 cm,BD=10 cm,CE=18 cm.
易错点 内心与外心概念混淆不清
10.如图,△ABC是圆的内接三角形,点P是△ABC的内心,∠A=50°,则∠BPC的度数是115°.
中档题
11.如图,△ABC的内心为I,连结AI并延长交△ABC的外接圆于D,则线段DI与DB的关系是(A)
A.DI=DB B.DI>DB
C.DI<DB D.不确定
12.如图,△ABC的三条边被⊙O所截得的三条线段相等,则下列说法正确的是(A)
A.点O是△ABC的内心
B.点O是△ABC的外心
C.△ABC是正三角形
D.△ABC是等腰三角形
13.如图,△ABC是一张周长为17 cm的三角形纸片,BC=5 cm,⊙O是它的内切圆,小明准备用剪刀在⊙O的右侧沿着与⊙O相切的任意一条直线MN剪下△AMN,则剪下的三角形的周长为(B)
A.12 cm B.7 cm
C.6 cm D.随直线MN的变化而变化
14.如图所示,PA,PB是⊙O的切线,切点分别为A,B,直线EF也是⊙O的切线,Q是切点,交PA,PB于E,F点.若PA=10 cm,则△PEF的周长为20cm;若∠APB=50°,则∠EOF的度数为65°.
15.如图,在扇形CAB中,CD⊥AB,垂足为D,⊙E是△ACD的内切圆,连结AE,BE,则∠AEB的度数为135°.
16.如图,AB,BC,CD分别与⊙O相切于点E,F,G,且AB∥CD,BO=6 cm,CO=8 cm.
(1)求证:BO⊥CO;(2)求BE和CG的长.
解:(1)证明:∵AB∥CD,
∴∠ABC+∠DCB=180°.
∵AB,BC,CD分别与⊙O相切于点E,F,G,
∴BO平分∠ABC,CO平分∠DCB.
∴∠OBC=∠ABC,∠OCB=∠DCB.
∴∠OBC+∠OCB=(∠ABC+∠DCB)
=×180°=90°.
∴∠BOC=90°.∴BO⊥CO.
(2)连结OF,则OF⊥BC,
∴Rt△BOF∽Rt△BCO.∴=.
∵在Rt△BOC中,BO=6 cm,CO=8 cm,
∴BC==10(cm).
∴=.∴BF=3.6 cm.
∵AB,BC,CD分别与⊙O相切,
∴BE=BF=3.6 cm,CG=CF.
∵CF=BC-BF=10-3.6=6.4(cm),
∴CG=CF=6.4 cm.
综合题
17.如图,PA,PB切⊙O于A,B两点,CD切⊙O于点E,交PA,PB于点C,D.若⊙O的半径为r,△PCD的周长等于3r,则tan∠APB的值是(B)
A. B.
C. D.
