沪教版高中物理选修3-3课件 2.4理想气体状态方程30张PPT
文档属性
| 名称 | 沪教版高中物理选修3-3课件 2.4理想气体状态方程30张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 827.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-03-20 16:17:47 | ||
图片预览










文档简介
课件30张PPT。理想气体状态方程[自学教材]1.定义
在 温度、 压强下都严格遵从气体实验定律的气体。
2.理想气体与实际气体
如图所示。任何任何[重点诠释] (1)从宏观上讲,理想气体是指在任何条件下始终遵守气体实验定律的气体,实际气体在压强不太大、温度不太低的条件下,都可视为理想气体。
(2)从微观上讲,理想气体应有如下性质:分子间除碰撞外无其他作用力;分子本身虽然有体积,但相对于分子所占空间,分子大小可忽略,即它所占据的空间认为都是可以被压缩的空间。显然这样的气体是不存在的,只是实际气体在一定程度上的近似。 (3)理想气体的微观本质是忽略了分子力,所以其状态无论怎么变化都没有分子力做功,即没有分子势能的变化,于是理想气体的内能只有分子动能,即一定质量的理想气体的内能完全由温度决定。
理想气体实际上是不存在的,它只是为了研究问题的方便,突出事物的主要因素,忽略次要因素而引入的一种理想化模型,就像力学中引入质点、电学中引入点电荷模型一样,这些理想化模型的引入使我们对物体规律的研究大大简化。1.关于理想气体,下面说法哪些是正确的 ( )
A.理想气体是严格遵守气体实验定律的气体模型
B.理想气体的分子没有体积
C.理想气体是一种理想模型,没有实际意义
D.实际气体在温度不太低、压强不太大的情况下,可
当成理想气体解析:理想气体是指严格遵守气体三定律的气体,实际的气体在压强不太高、温度不太低时可以认为是理想气体,A、D对。理想气体分子间没有分子力,但分子有大小,B错。
答案:AD[自学教材]乘积比值质量[重点诠释]2.应用状态方程解题的一般步骤
(1)明确研究对象,即一定质量的理想气体;
(2)确定气体在始末状态的参量p1、V1、T1及p2、V2、T2;
(3)由状态方程列式求解;
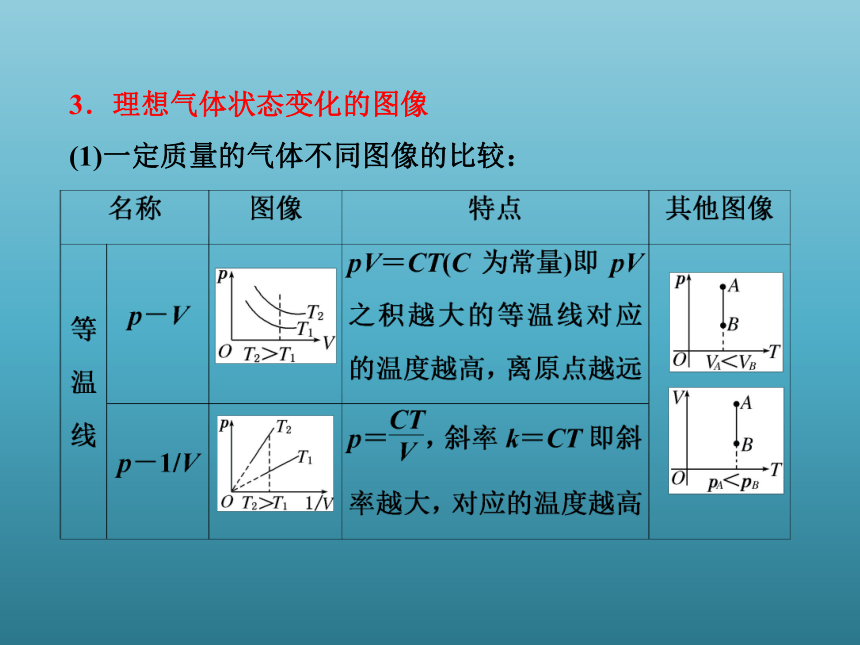
(4)讨论结果的合理性。3.理想气体状态变化的图像
(1)一定质量的气体不同图像的比较: (2)一般状态变化图像的处理方法:
基本方法,化“一般”为“特殊”,如图是一定质量的某种气体的状态变化过程A→B→C→A。 在V-T图线上,等压线是一簇延长线过原点的直线,过A、B、C三点作三条等压线分别表示三个等压过程pA′端封闭一端开口的U形玻璃管,当t1=31 ℃,
大气压强p0=76 cmHg时,两管水银面相平,
这时左管被封闭的气柱长L1=8 cm,则:
(1)当温度t2是多少时,左管气柱L2为9 cm?
(2)当温度达到上问中的温度t2时,为使左管气柱长L为
8 cm,应在右管中加入多长的水银柱? [思路点拨] 水银柱封闭气体的情况,压强的单位直接用cmHg表示,封闭气体是气柱,体积用气柱的长度与面积S来表示,这样做的目的是简化计算。[答案] (1)78 ℃ (2)11.75 cm1.为了测定湖的深度,将一根试管开口向下缓缓压至湖底,
测得进入管中的水的高度为管长的3/4,湖底水温为4 ℃,湖面水温为10 ℃,大气压强76 cmHg。求湖深多少?答案:30.1 m [例2] 房间的容积为20 m3,在温度为7 ℃、大气压强为9.8×104 Pa时,室内空气质量是25 kg。当温度升高到27 ℃,大气压强变为1.0×105 Pa时,室内空气的质量是多少?
[思路点拨] 室内气体的温度、压强均发生了变化,后来气体的体积不一定再是20 m3,可能增大,即有气体从房间内跑出,可能减小,即有气体流入房间内,因此仍以原25 kg气体,通过计算体积确定20 m3的体积中还有多少气体,再计算气体的质量。[答案] 23.8 kg [借题发挥]
本题是变质量问题,如果我们通过恰当地选取研究对象,可以使变质量问题转化为定质量问题,运用理想气体状态方程求解。2.钢筒内装有3 kg气体,当温度为-23 ℃时,压强为4 atm,
如果用掉1 kg气体后温度升高到27 ℃,求筒内气体压强?答案:3.2 atm [例3] 使一定质量的理想气体按图甲中箭头所示的顺序变化,图中BC段是以纵轴和横轴为渐近线的双曲线。 (1)已知气体在状态A的温度TA=300 K,求气体在状态B、C和D的温度各是多少。
(2)将上述状态变化过程在图乙中画成用体积V和温度T表示的图线(图中要标明A、B、C、D四点,并且要画箭头表示变化的方向),且说明每段图线各表示什么过程。
[思路点拨] 解答本题可按以下思路分析:[答案] (1)600 K 600 K 300 K (2)见解析在如图所示的p-T图中画出A→B→C→D状态变化图像。解析:由以上计算可知:
pA=4 atm,TA=300 K,
pB=4 atm,TB=600 K,
pC=2 atm,TC=600 K,
pD=2 atm,TD=300 K,所以其状态变化过程的p-T图线如图所示:答案:见解析图
在 温度、 压强下都严格遵从气体实验定律的气体。
2.理想气体与实际气体
如图所示。任何任何[重点诠释] (1)从宏观上讲,理想气体是指在任何条件下始终遵守气体实验定律的气体,实际气体在压强不太大、温度不太低的条件下,都可视为理想气体。
(2)从微观上讲,理想气体应有如下性质:分子间除碰撞外无其他作用力;分子本身虽然有体积,但相对于分子所占空间,分子大小可忽略,即它所占据的空间认为都是可以被压缩的空间。显然这样的气体是不存在的,只是实际气体在一定程度上的近似。 (3)理想气体的微观本质是忽略了分子力,所以其状态无论怎么变化都没有分子力做功,即没有分子势能的变化,于是理想气体的内能只有分子动能,即一定质量的理想气体的内能完全由温度决定。
理想气体实际上是不存在的,它只是为了研究问题的方便,突出事物的主要因素,忽略次要因素而引入的一种理想化模型,就像力学中引入质点、电学中引入点电荷模型一样,这些理想化模型的引入使我们对物体规律的研究大大简化。1.关于理想气体,下面说法哪些是正确的 ( )
A.理想气体是严格遵守气体实验定律的气体模型
B.理想气体的分子没有体积
C.理想气体是一种理想模型,没有实际意义
D.实际气体在温度不太低、压强不太大的情况下,可
当成理想气体解析:理想气体是指严格遵守气体三定律的气体,实际的气体在压强不太高、温度不太低时可以认为是理想气体,A、D对。理想气体分子间没有分子力,但分子有大小,B错。
答案:AD[自学教材]乘积比值质量[重点诠释]2.应用状态方程解题的一般步骤
(1)明确研究对象,即一定质量的理想气体;
(2)确定气体在始末状态的参量p1、V1、T1及p2、V2、T2;
(3)由状态方程列式求解;
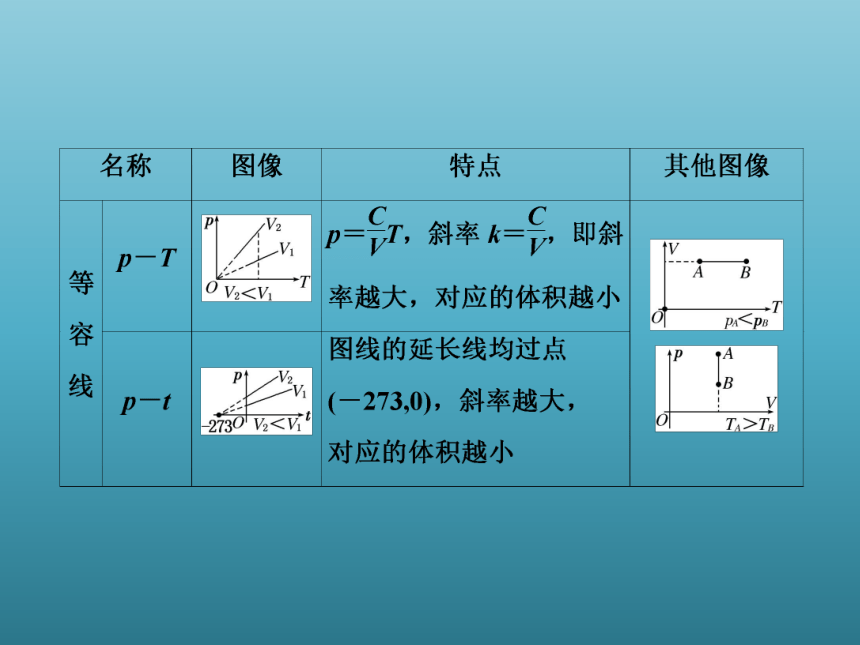
(4)讨论结果的合理性。3.理想气体状态变化的图像
(1)一定质量的气体不同图像的比较: (2)一般状态变化图像的处理方法:
基本方法,化“一般”为“特殊”,如图是一定质量的某种气体的状态变化过程A→B→C→A。 在V-T图线上,等压线是一簇延长线过原点的直线,过A、B、C三点作三条等压线分别表示三个等压过程pA′
大气压强p0=76 cmHg时,两管水银面相平,
这时左管被封闭的气柱长L1=8 cm,则:
(1)当温度t2是多少时,左管气柱L2为9 cm?
(2)当温度达到上问中的温度t2时,为使左管气柱长L为
8 cm,应在右管中加入多长的水银柱? [思路点拨] 水银柱封闭气体的情况,压强的单位直接用cmHg表示,封闭气体是气柱,体积用气柱的长度与面积S来表示,这样做的目的是简化计算。[答案] (1)78 ℃ (2)11.75 cm1.为了测定湖的深度,将一根试管开口向下缓缓压至湖底,
测得进入管中的水的高度为管长的3/4,湖底水温为4 ℃,湖面水温为10 ℃,大气压强76 cmHg。求湖深多少?答案:30.1 m [例2] 房间的容积为20 m3,在温度为7 ℃、大气压强为9.8×104 Pa时,室内空气质量是25 kg。当温度升高到27 ℃,大气压强变为1.0×105 Pa时,室内空气的质量是多少?
[思路点拨] 室内气体的温度、压强均发生了变化,后来气体的体积不一定再是20 m3,可能增大,即有气体从房间内跑出,可能减小,即有气体流入房间内,因此仍以原25 kg气体,通过计算体积确定20 m3的体积中还有多少气体,再计算气体的质量。[答案] 23.8 kg [借题发挥]
本题是变质量问题,如果我们通过恰当地选取研究对象,可以使变质量问题转化为定质量问题,运用理想气体状态方程求解。2.钢筒内装有3 kg气体,当温度为-23 ℃时,压强为4 atm,
如果用掉1 kg气体后温度升高到27 ℃,求筒内气体压强?答案:3.2 atm [例3] 使一定质量的理想气体按图甲中箭头所示的顺序变化,图中BC段是以纵轴和横轴为渐近线的双曲线。 (1)已知气体在状态A的温度TA=300 K,求气体在状态B、C和D的温度各是多少。
(2)将上述状态变化过程在图乙中画成用体积V和温度T表示的图线(图中要标明A、B、C、D四点,并且要画箭头表示变化的方向),且说明每段图线各表示什么过程。
[思路点拨] 解答本题可按以下思路分析:[答案] (1)600 K 600 K 300 K (2)见解析在如图所示的p-T图中画出A→B→C→D状态变化图像。解析:由以上计算可知:
pA=4 atm,TA=300 K,
pB=4 atm,TB=600 K,
pC=2 atm,TC=600 K,
pD=2 atm,TD=300 K,所以其状态变化过程的p-T图线如图所示:答案:见解析图
同课章节目录
- 第一章用统计思想研究分子运动
- 1.1一种新的研究方法
- 1.2走过分子世界
- 1.3 分子热运动
- 1.4无序中的有序
- 1.5用统计思想解释分子运动的宏观表现
- 1.6物体的内能
- 第二章气体定律与人类生活
- 2.1气体的状态
- 2.2玻意耳定律
- 2.3查理定律和盖·吕萨克定律
- 2.4 理想气体状态方程
- 2.5空气的湿度与人类生活
- 第三章固体、液体与新材料
- 3.1研究固体的性质
- 3.2研究液体的表面性质
- 3.3液晶与显示器
- 3.4半导体材料和纳米材料
- 第四章热力学定律与能量守恒
- 4.1热力学第一定律
- 4.2能量守恒定律的发现历程
- 4.3热力学第二定律
- 4.4描述无序程度的物理量
- 第五章能源与可持续发展
- 5.1能源利用与环境污染
- 5.2能源开发与环境保护
- 5.3节约能源、保护资源与可持续发展
