2020春华师大版九下数学27.2与圆有关的位置关系同步测试含答案
文档属性
| 名称 | 2020春华师大版九下数学27.2与圆有关的位置关系同步测试含答案 |
|
|
| 格式 | zip | ||
| 文件大小 | 219.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-20 00:00:00 | ||
图片预览



文档简介
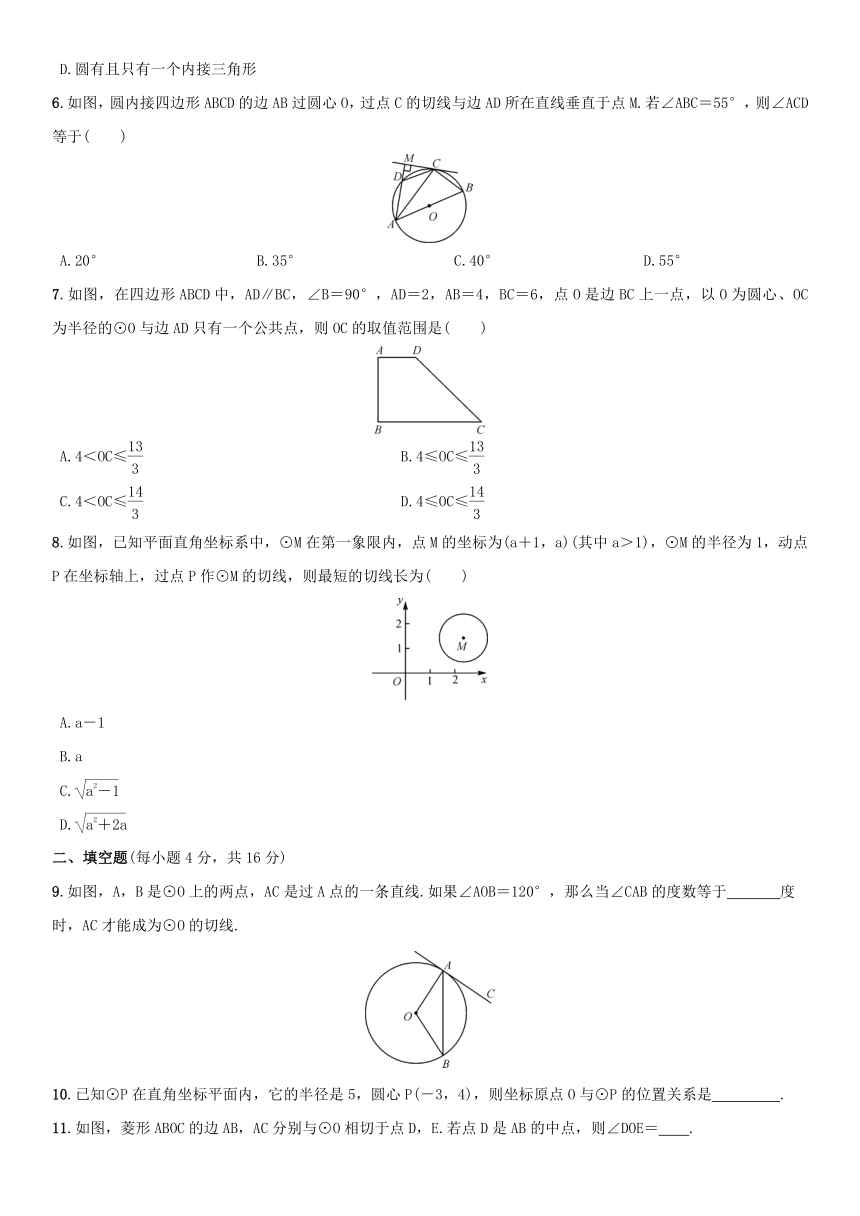
2020春华师大版九下数学27.2与圆有关的位置关系同步测试(学生版)
(时间:40分钟 满分:100分)
一、选择题(每小题4分,共32分)
1.圆的半径为5 cm,圆心到一条直线的距离是7 cm,则直线与圆( )
A.相交 B.相切
C.相离 D.无法确定
2.如图,已知⊙O的半径为5,直线EF经过⊙O上一点P(点E,F在点P的两旁),下列条件能判定直线EF与⊙O相切的是( )
A.OP=5
B.OE=OF
C.O到直线EF的距离是4
D.OP⊥EF
3.如图,AB是⊙O的直径,AC是⊙O的切线,A为切点,BC与⊙O交于点D,连结OD.若∠C=50°,则∠AOD的度数为( )
A.40° B.50° C.80° D.100°
4.如图所示,PA,PB是⊙O的切线,且∠APB=40°,下列说法不正确的是( )
A.PA=PB B.∠APO=20°
C.∠OBP=70° D.∠AOP=70°
5.下列说法中,正确的是( )
A.三点确定一个圆
B.三角形有且只有一个外接圆
C.四边形都有一个外接圆
D.圆有且只有一个内接三角形
6.如图,圆内接四边形ABCD的边AB过圆心O,过点C的切线与边AD所在直线垂直于点M.若∠ABC=55°,则∠ACD等于( )
A.20° B.35° C.40° D.55°
7.如图,在四边形ABCD中,AD∥BC,∠B=90°,AD=2,AB=4,BC=6,点O是边BC上一点,以O为圆心、OC为半径的⊙O与边AD只有一个公共点,则OC的取值范围是( )
A.4<OC≤ B.4≤OC≤
C.4<OC≤ D.4≤OC≤
8.如图,已知平面直角坐标系中,⊙M在第一象限内,点M的坐标为(a+1,a)(其中a>1),⊙M的半径为1,动点P在坐标轴上,过点P作⊙M的切线,则最短的切线长为( )
A.a-1
B.a
C.
D.
二、填空题(每小题4分,共16分)
9.如图,A,B是⊙O上的两点,AC是过A点的一条直线.如果∠AOB=120°,那么当∠CAB的度数等于 度时,AC才能成为⊙O的切线.
10.已知⊙P在直角坐标平面内,它的半径是5,圆心P(-3,4),则坐标原点O与⊙P的位置关系是 .
11.如图,菱形ABOC的边AB,AC分别与⊙O相切于点D,E.若点D是AB的中点,则∠DOE= .
12.如图,在Rt△ABC中,∠ACB=90°,I为Rt△ABC的内心,过点I作ID∥BC,交斜边AB于点D,连结CI,则∠CID= °.
三、解答题(共52分)
13.(10分)设⊙O的半径为r,圆心O到直线的距离为d,且直线与⊙O相切.d,r是一元二次方程(m+9)x2-(m+6)x+1=0的两根,求m的值.
14.(12分)如图,在△ABC中,∠C=90°.尺规作图:作⊙O,使⊙O与AB,BC都相切,且圆心O在AC边上;设⊙O与AB的切点为D,⊙O的半径为3,且=,求AB的长.
15.(14分)如图,AB是⊙O的直径,点C在AB的延长线上,AD平分∠CAE交⊙O于点D,且AE⊥CD,垂足为E.
(1)求证:直线CE是⊙O的切线;
(2)若BC=3,CD=3,求弦AD的长.
16.(16分)如图,AB是半圆O的直径,点P是半圆上不与点A,B重合的动点,PC∥AB,点M是OP中点.
(1)求证:四边形OBCP是平行四边形;
(2)填空:
①当∠BOP= 时,四边形AOCP是菱形;
②连结BP,当∠ABP= 时,PC是⊙O的切线.
2020春华师大版九下数学27.2与圆有关的位置关系同步测试(教师版)
(时间:40分钟 满分:100分)
一、选择题(每小题4分,共32分)
1.圆的半径为5 cm,圆心到一条直线的距离是7 cm,则直线与圆(C)
A.相交 B.相切
C.相离 D.无法确定
2.如图,已知⊙O的半径为5,直线EF经过⊙O上一点P(点E,F在点P的两旁),下列条件能判定直线EF与⊙O相切的是(D)
A.OP=5
B.OE=OF
C.O到直线EF的距离是4
D.OP⊥EF
3.如图,AB是⊙O的直径,AC是⊙O的切线,A为切点,BC与⊙O交于点D,连结OD.若∠C=50°,则∠AOD的度数为(C)
A.40° B.50° C.80° D.100°
4.如图所示,PA,PB是⊙O的切线,且∠APB=40°,下列说法不正确的是(C)
A.PA=PB B.∠APO=20°
C.∠OBP=70° D.∠AOP=70°
5.下列说法中,正确的是(B)
A.三点确定一个圆
B.三角形有且只有一个外接圆
C.四边形都有一个外接圆
D.圆有且只有一个内接三角形
6.如图,圆内接四边形ABCD的边AB过圆心O,过点C的切线与边AD所在直线垂直于点M.若∠ABC=55°,则∠ACD等于(A)
A.20° B.35° C.40° D.55°
7.如图,在四边形ABCD中,AD∥BC,∠B=90°,AD=2,AB=4,BC=6,点O是边BC上一点,以O为圆心、OC为半径的⊙O与边AD只有一个公共点,则OC的取值范围是(B)
A.4<OC≤ B.4≤OC≤
C.4<OC≤ D.4≤OC≤
8.如图,已知平面直角坐标系中,⊙M在第一象限内,点M的坐标为(a+1,a)(其中a>1),⊙M的半径为1,动点P在坐标轴上,过点P作⊙M的切线,则最短的切线长为(C)
A.a-1
B.a
C.
D.
二、填空题(每小题4分,共16分)
9.如图,A,B是⊙O上的两点,AC是过A点的一条直线.如果∠AOB=120°,那么当∠CAB的度数等于60度时,AC才能成为⊙O的切线.
10.已知⊙P在直角坐标平面内,它的半径是5,圆心P(-3,4),则坐标原点O与⊙P的位置关系是点O在⊙P上.
11.如图,菱形ABOC的边AB,AC分别与⊙O相切于点D,E.若点D是AB的中点,则∠DOE=60°.
12.如图,在Rt△ABC中,∠ACB=90°,I为Rt△ABC的内心,过点I作ID∥BC,交斜边AB于点D,连结CI,则∠CID=135°.
三、解答题(共52分)
13.(10分)设⊙O的半径为r,圆心O到直线的距离为d,且直线与⊙O相切.d,r是一元二次方程(m+9)x2-(m+6)x+1=0的两根,求m的值.
解:∵⊙O的半径为r,圆心O到直线的距离为d,且直线与⊙O相切,
∴d=r.
∵d,r是一元二次方程(m+9)x2-(m+6)x+1=0的两根,
∴Δ=0,
即[-(m+6)]2-4(m+9)·1=0.
解得m=0或m=-8.
当m=-8时,x=-1,不符合题意,舍去.
故m=0.
14.(12分)如图,在△ABC中,∠C=90°.尺规作图:作⊙O,使⊙O与AB,BC都相切,且圆心O在AC边上;设⊙O与AB的切点为D,⊙O的半径为3,且=,求AB的长.
解:(1)作∠ABC的平分线BP,交AC于点O,以O为圆心,OC的长为半径作圆,则⊙O即是所求图形.
(2)设AD=2x,BD=3x,则BC=3x,AB=5x,
在Rt△ABC中,AC==4x.
∵DO=CO=3,∴AO=4x-3.
在Rt△AOD中,AD2+DO2=AO2,
即(2x)2+32=(4x-3)2.
解得x=2或x=0(舍去).
∴AB=5×2=10.
15.(14分)如图,AB是⊙O的直径,点C在AB的延长线上,AD平分∠CAE交⊙O于点D,且AE⊥CD,垂足为E.
(1)求证:直线CE是⊙O的切线;
(2)若BC=3,CD=3,求弦AD的长.
解:(1)证明:连结OD.
∵AD平分∠CAE,
∴∠CAD=∠EAD.
∵OA=OD,
∴∠CAD=∠ODA.
∴∠EAD=∠ODA.
∴OD∥AE.
∵AE⊥DC,
∴OD⊥CE.
又∵OD是⊙O的半径,
∴CE是⊙O的切线.
(2)连结BD.∵∠CDO=∠ADB=90°,
∴∠ODA=∠CDB=∠CAD.
∵∠C=∠C,
∴△CDB∽△CAD.
∴==,即==.
∴CA=6,BD=AD.
∴AB=CA-BC=3.
在Rt△ADB中,AD2+BD2=AB2,即AD2+(AD)2=32,
∴AD=(负值舍去).
16.(16分)如图,AB是半圆O的直径,点P是半圆上不与点A,B重合的动点,PC∥AB,点M是OP中点.
(1)求证:四边形OBCP是平行四边形;
(2)填空:
①当∠BOP=120°时,四边形AOCP是菱形;
②连结BP,当∠ABP=45°时,PC是⊙O的切线.
证明:∵PC∥AB,
∴∠PCM=∠OAM,∠CPM=∠AOM.
∵点M是OP的中点,∴OM=PM.
在△CPM和△AOM中,
∴△CPM≌△AOM(AAS).
∴PC=OA.
∵AB是半圆O的直径,
∴OA=OB.
∴PC=OB.
又∵PC∥AB,
∴四边形OBCP是平行四边形.
(时间:40分钟 满分:100分)
一、选择题(每小题4分,共32分)
1.圆的半径为5 cm,圆心到一条直线的距离是7 cm,则直线与圆( )
A.相交 B.相切
C.相离 D.无法确定
2.如图,已知⊙O的半径为5,直线EF经过⊙O上一点P(点E,F在点P的两旁),下列条件能判定直线EF与⊙O相切的是( )
A.OP=5
B.OE=OF
C.O到直线EF的距离是4
D.OP⊥EF
3.如图,AB是⊙O的直径,AC是⊙O的切线,A为切点,BC与⊙O交于点D,连结OD.若∠C=50°,则∠AOD的度数为( )
A.40° B.50° C.80° D.100°
4.如图所示,PA,PB是⊙O的切线,且∠APB=40°,下列说法不正确的是( )
A.PA=PB B.∠APO=20°
C.∠OBP=70° D.∠AOP=70°
5.下列说法中,正确的是( )
A.三点确定一个圆
B.三角形有且只有一个外接圆
C.四边形都有一个外接圆
D.圆有且只有一个内接三角形
6.如图,圆内接四边形ABCD的边AB过圆心O,过点C的切线与边AD所在直线垂直于点M.若∠ABC=55°,则∠ACD等于( )
A.20° B.35° C.40° D.55°
7.如图,在四边形ABCD中,AD∥BC,∠B=90°,AD=2,AB=4,BC=6,点O是边BC上一点,以O为圆心、OC为半径的⊙O与边AD只有一个公共点,则OC的取值范围是( )
A.4<OC≤ B.4≤OC≤
C.4<OC≤ D.4≤OC≤
8.如图,已知平面直角坐标系中,⊙M在第一象限内,点M的坐标为(a+1,a)(其中a>1),⊙M的半径为1,动点P在坐标轴上,过点P作⊙M的切线,则最短的切线长为( )
A.a-1
B.a
C.
D.
二、填空题(每小题4分,共16分)
9.如图,A,B是⊙O上的两点,AC是过A点的一条直线.如果∠AOB=120°,那么当∠CAB的度数等于 度时,AC才能成为⊙O的切线.
10.已知⊙P在直角坐标平面内,它的半径是5,圆心P(-3,4),则坐标原点O与⊙P的位置关系是 .
11.如图,菱形ABOC的边AB,AC分别与⊙O相切于点D,E.若点D是AB的中点,则∠DOE= .
12.如图,在Rt△ABC中,∠ACB=90°,I为Rt△ABC的内心,过点I作ID∥BC,交斜边AB于点D,连结CI,则∠CID= °.
三、解答题(共52分)
13.(10分)设⊙O的半径为r,圆心O到直线的距离为d,且直线与⊙O相切.d,r是一元二次方程(m+9)x2-(m+6)x+1=0的两根,求m的值.
14.(12分)如图,在△ABC中,∠C=90°.尺规作图:作⊙O,使⊙O与AB,BC都相切,且圆心O在AC边上;设⊙O与AB的切点为D,⊙O的半径为3,且=,求AB的长.
15.(14分)如图,AB是⊙O的直径,点C在AB的延长线上,AD平分∠CAE交⊙O于点D,且AE⊥CD,垂足为E.
(1)求证:直线CE是⊙O的切线;
(2)若BC=3,CD=3,求弦AD的长.
16.(16分)如图,AB是半圆O的直径,点P是半圆上不与点A,B重合的动点,PC∥AB,点M是OP中点.
(1)求证:四边形OBCP是平行四边形;
(2)填空:
①当∠BOP= 时,四边形AOCP是菱形;
②连结BP,当∠ABP= 时,PC是⊙O的切线.
2020春华师大版九下数学27.2与圆有关的位置关系同步测试(教师版)
(时间:40分钟 满分:100分)
一、选择题(每小题4分,共32分)
1.圆的半径为5 cm,圆心到一条直线的距离是7 cm,则直线与圆(C)
A.相交 B.相切
C.相离 D.无法确定
2.如图,已知⊙O的半径为5,直线EF经过⊙O上一点P(点E,F在点P的两旁),下列条件能判定直线EF与⊙O相切的是(D)
A.OP=5
B.OE=OF
C.O到直线EF的距离是4
D.OP⊥EF
3.如图,AB是⊙O的直径,AC是⊙O的切线,A为切点,BC与⊙O交于点D,连结OD.若∠C=50°,则∠AOD的度数为(C)
A.40° B.50° C.80° D.100°
4.如图所示,PA,PB是⊙O的切线,且∠APB=40°,下列说法不正确的是(C)
A.PA=PB B.∠APO=20°
C.∠OBP=70° D.∠AOP=70°
5.下列说法中,正确的是(B)
A.三点确定一个圆
B.三角形有且只有一个外接圆
C.四边形都有一个外接圆
D.圆有且只有一个内接三角形
6.如图,圆内接四边形ABCD的边AB过圆心O,过点C的切线与边AD所在直线垂直于点M.若∠ABC=55°,则∠ACD等于(A)
A.20° B.35° C.40° D.55°
7.如图,在四边形ABCD中,AD∥BC,∠B=90°,AD=2,AB=4,BC=6,点O是边BC上一点,以O为圆心、OC为半径的⊙O与边AD只有一个公共点,则OC的取值范围是(B)
A.4<OC≤ B.4≤OC≤
C.4<OC≤ D.4≤OC≤
8.如图,已知平面直角坐标系中,⊙M在第一象限内,点M的坐标为(a+1,a)(其中a>1),⊙M的半径为1,动点P在坐标轴上,过点P作⊙M的切线,则最短的切线长为(C)
A.a-1
B.a
C.
D.
二、填空题(每小题4分,共16分)
9.如图,A,B是⊙O上的两点,AC是过A点的一条直线.如果∠AOB=120°,那么当∠CAB的度数等于60度时,AC才能成为⊙O的切线.
10.已知⊙P在直角坐标平面内,它的半径是5,圆心P(-3,4),则坐标原点O与⊙P的位置关系是点O在⊙P上.
11.如图,菱形ABOC的边AB,AC分别与⊙O相切于点D,E.若点D是AB的中点,则∠DOE=60°.
12.如图,在Rt△ABC中,∠ACB=90°,I为Rt△ABC的内心,过点I作ID∥BC,交斜边AB于点D,连结CI,则∠CID=135°.
三、解答题(共52分)
13.(10分)设⊙O的半径为r,圆心O到直线的距离为d,且直线与⊙O相切.d,r是一元二次方程(m+9)x2-(m+6)x+1=0的两根,求m的值.
解:∵⊙O的半径为r,圆心O到直线的距离为d,且直线与⊙O相切,
∴d=r.
∵d,r是一元二次方程(m+9)x2-(m+6)x+1=0的两根,
∴Δ=0,
即[-(m+6)]2-4(m+9)·1=0.
解得m=0或m=-8.
当m=-8时,x=-1,不符合题意,舍去.
故m=0.
14.(12分)如图,在△ABC中,∠C=90°.尺规作图:作⊙O,使⊙O与AB,BC都相切,且圆心O在AC边上;设⊙O与AB的切点为D,⊙O的半径为3,且=,求AB的长.
解:(1)作∠ABC的平分线BP,交AC于点O,以O为圆心,OC的长为半径作圆,则⊙O即是所求图形.
(2)设AD=2x,BD=3x,则BC=3x,AB=5x,
在Rt△ABC中,AC==4x.
∵DO=CO=3,∴AO=4x-3.
在Rt△AOD中,AD2+DO2=AO2,
即(2x)2+32=(4x-3)2.
解得x=2或x=0(舍去).
∴AB=5×2=10.
15.(14分)如图,AB是⊙O的直径,点C在AB的延长线上,AD平分∠CAE交⊙O于点D,且AE⊥CD,垂足为E.
(1)求证:直线CE是⊙O的切线;
(2)若BC=3,CD=3,求弦AD的长.
解:(1)证明:连结OD.
∵AD平分∠CAE,
∴∠CAD=∠EAD.
∵OA=OD,
∴∠CAD=∠ODA.
∴∠EAD=∠ODA.
∴OD∥AE.
∵AE⊥DC,
∴OD⊥CE.
又∵OD是⊙O的半径,
∴CE是⊙O的切线.
(2)连结BD.∵∠CDO=∠ADB=90°,
∴∠ODA=∠CDB=∠CAD.
∵∠C=∠C,
∴△CDB∽△CAD.
∴==,即==.
∴CA=6,BD=AD.
∴AB=CA-BC=3.
在Rt△ADB中,AD2+BD2=AB2,即AD2+(AD)2=32,
∴AD=(负值舍去).
16.(16分)如图,AB是半圆O的直径,点P是半圆上不与点A,B重合的动点,PC∥AB,点M是OP中点.
(1)求证:四边形OBCP是平行四边形;
(2)填空:
①当∠BOP=120°时,四边形AOCP是菱形;
②连结BP,当∠ABP=45°时,PC是⊙O的切线.
证明:∵PC∥AB,
∴∠PCM=∠OAM,∠CPM=∠AOM.
∵点M是OP的中点,∴OM=PM.
在△CPM和△AOM中,
∴△CPM≌△AOM(AAS).
∴PC=OA.
∵AB是半圆O的直径,
∴OA=OB.
∴PC=OB.
又∵PC∥AB,
∴四边形OBCP是平行四边形.
