沪教版高中物理选修3-5课件 第1章 碰撞与动量守恒 复习课件26张PPT
文档属性
| 名称 | 沪教版高中物理选修3-5课件 第1章 碰撞与动量守恒 复习课件26张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 400.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-03-20 17:58:41 | ||
图片预览

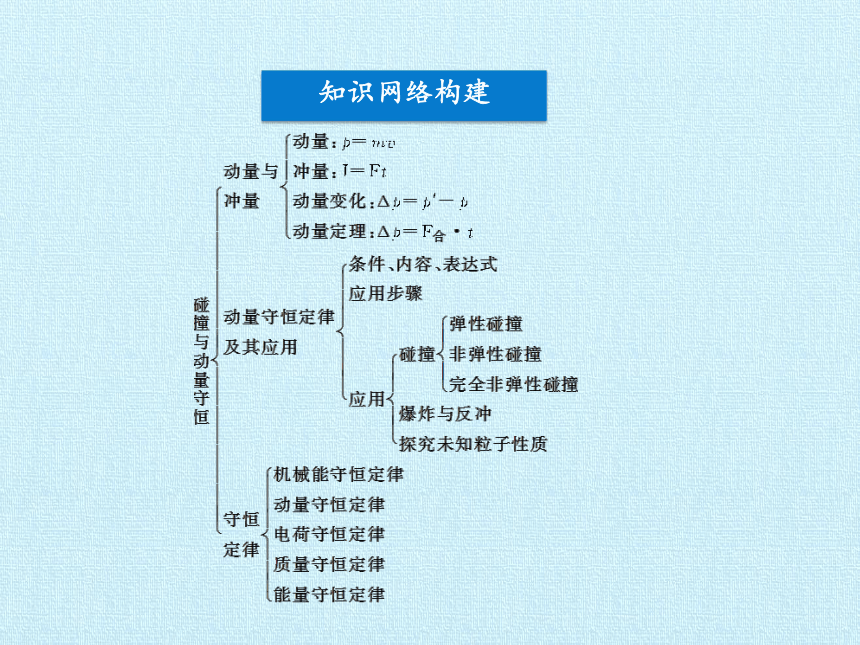







文档简介
课件26张PPT。第1章 碰撞与动量守恒
复习课件知识网络构建专题归纳总结 动量定理的典型应用分五个方面:第一,解释现象;第二,常规应用,牛顿定律能解决的问题动量定理均可,且简便;第三,解决变力问题;第四,应用于多过程问题;第五,应用于连续不断的流体. 一个人做“蹦极”运动,用原长为20 m的橡皮绳拴住身体,若此人质量为50 kg,从50 m高处由静止跳下,至运动停止瞬间所用时间为4 s,则橡皮绳对人的平均作用力约为________N(g取10 m/s2).【答案】 1000 对于两个以上的物体组成的物体系,由于物体较多,相互作用的情况也不尽相同,作用过程较为复杂,虽然仍可对初末状态建立动量守恒的关系式,但因未知条件多往往无法求解.这时往往要根据作用过程中的不同阶段,建立多个动量守恒定律方程,或将系统内的物体按作用的关系分成几个小系统,分别建立动量守恒定律方程. 解这类问题时应注意:①正确分析作用过程中各物体状态的变化情况,建立物理模型;②分清作用过程的各个阶段和联系各个阶段的状态量;③合理选取研究对象,既要符合动量守恒的条件,又要方便解题。 两只船平行逆向航行,航线邻近,当它们头尾相齐时,同时将每只船上质量为m=50 kg的麻袋垂直航行方向投到对面一只船上去,结果载重较小的一只船停了下来,另一只船则以v=8.5 m/s的速度沿原方向航行.设两只船及各自船上的货物总质量各为m1=500 kg,m2=1000 kg,则在交换麻袋前两只船的速度为多少?(不计水的阻力)【精讲精析】 设小船、大船原速度大小为v1、v2,选取小船和从大船上投过的麻袋为系统,如图1-1所示,并以小船的速度方向为正方向,根据动量守恒有:(m1-m)v1-mv2=0 ①:选取大船和从小船投过的麻袋为系统,有-(m2-m)v2+mv1=-m2v②:由①②式解得:v1=1 m/s,v2=9 m/s。图1-1【答案】 v小=1 m/s v大=9 m/s
【方法总结】 可见解此题的关键是正确选择研究系统,注意分析初、末状态. 动量守恒定律是力学中的一个重要规律,在运用动量守恒定律解题时,常会遇到相互作用的几个物体间的临界问题,求解这类问题要注意分析临界状态,把握相关的临界条件.现把与应用动量守恒定律解题相关的临界问题做初步的分析和讨论.1.涉及弹簧的临界问题
对于由弹簧组成的系统,在物体间发生相互作用的过程中,当弹簧被压缩到最短(或拉伸到最长)时,弹簧两端的两个物体的速度必相等。
2.涉及追碰的临界问题
两个在光滑水平面上做匀速直线运动的物体,甲物体追上乙物体的条件是甲物体的速度v甲必须大于乙物体的速度v乙,即v甲>v乙,而甲物体刚好追不上乙物体的临界条件是v甲=v乙。3.涉及子弹打木块的临界问题
子弹打木块是一种常见的模型.子弹刚好击穿木块的临界条件为子弹穿出时的速度与木块的速度相同. 甲、乙两个小孩各乘一辆冰车在水平冰面上游戏,甲和他的冰车的总质量为M=30 kg,乙和他的冰车的总质量也是30 kg.甲推着一个质量m=15 kg的箱子,和他一起以大小为v0=2 m/s的速度滑行,乙以同样大小的速度迎面滑来,为了避免相碰,甲突然将箱子沿冰面推给乙,箱子滑到乙处时乙迅速把它抓住.若不计冰面的摩擦力,求甲至少要以多大的速度(相对于冰面)将箱子推出,才能避免与乙相撞?【精讲精析】 当甲把箱子推出后,甲的运动存在三种可能:①继续向前,方向不变;②停止运动;③反向运动.由动量守恒定律可知,第一种可能若能实现目标,则箱子获得的速度最小.设箱子推出后的速度为v,取甲运动方向为正方向,则对甲和箱子在推出过程中运用动量守恒定律有(M+m)v0=Mv甲+mv箱子推出后,被乙抓住,为避免甲、乙相撞,则乙必须后退,对乙和箱子运用动量守恒定律得:
mv-Mv0=(M+m)v乙
要使甲、乙不相撞,并使推出箱子的速度最小的临界条件为v甲=v乙.
解以上三式得v=5.2 m/s.
【答案】 5.2 m/s【规律总结】 在处理碰撞中动量守恒的问题时,要抓住几个关键点,一是选取动量守恒的系统,二是弄清碰撞的类型,三是碰撞过程中存在的关系:能量转化关系、几何关系、速度关系等,如本题中的速度关系就是典型问题.碰撞问题是动量与能量结合求解的典型问题.应用动量和能量观点解决问题的优点都是不必过细分析物理过程的细节,但要明确指出所研究的过程和状态. 用轻弹簧相连的质量均为2 kg的A、B两物块都以v=6 m/s的速度在光滑的水平面上运动,弹簧处于原长,质量为4 kg的物块C在前方静止,如图1-2所示.B与C碰后二者粘在一起运动.在以后的运动中,求:图1-2(1)当弹簧的弹性势能最大时,物体A的速度是多大?
(2)弹性势能最大值是多少?
(3)A的速度可能向左吗?为什么?【精讲精析】 (1)设弹性势能最大时,A的速度为v1,
当A、B、C三个物块同速时,弹性势能最大,由动量守恒定律有:
(mA+mB)v=(mA+mB+mC)v1
解得:v1=3 m/s。【答案】 (1)3 m/s (2)12 J (3)见精讲精析
【规律总结】 弹簧类问题多数要出现“压缩到最短”“拉伸到最长”“最大弹性势能”等关键词,这种情况下一般都意味着系统速度相等.要善于理解、抓住这类隐含条件.谢 谢
复习课件知识网络构建专题归纳总结 动量定理的典型应用分五个方面:第一,解释现象;第二,常规应用,牛顿定律能解决的问题动量定理均可,且简便;第三,解决变力问题;第四,应用于多过程问题;第五,应用于连续不断的流体. 一个人做“蹦极”运动,用原长为20 m的橡皮绳拴住身体,若此人质量为50 kg,从50 m高处由静止跳下,至运动停止瞬间所用时间为4 s,则橡皮绳对人的平均作用力约为________N(g取10 m/s2).【答案】 1000 对于两个以上的物体组成的物体系,由于物体较多,相互作用的情况也不尽相同,作用过程较为复杂,虽然仍可对初末状态建立动量守恒的关系式,但因未知条件多往往无法求解.这时往往要根据作用过程中的不同阶段,建立多个动量守恒定律方程,或将系统内的物体按作用的关系分成几个小系统,分别建立动量守恒定律方程. 解这类问题时应注意:①正确分析作用过程中各物体状态的变化情况,建立物理模型;②分清作用过程的各个阶段和联系各个阶段的状态量;③合理选取研究对象,既要符合动量守恒的条件,又要方便解题。 两只船平行逆向航行,航线邻近,当它们头尾相齐时,同时将每只船上质量为m=50 kg的麻袋垂直航行方向投到对面一只船上去,结果载重较小的一只船停了下来,另一只船则以v=8.5 m/s的速度沿原方向航行.设两只船及各自船上的货物总质量各为m1=500 kg,m2=1000 kg,则在交换麻袋前两只船的速度为多少?(不计水的阻力)【精讲精析】 设小船、大船原速度大小为v1、v2,选取小船和从大船上投过的麻袋为系统,如图1-1所示,并以小船的速度方向为正方向,根据动量守恒有:(m1-m)v1-mv2=0 ①:选取大船和从小船投过的麻袋为系统,有-(m2-m)v2+mv1=-m2v②:由①②式解得:v1=1 m/s,v2=9 m/s。图1-1【答案】 v小=1 m/s v大=9 m/s
【方法总结】 可见解此题的关键是正确选择研究系统,注意分析初、末状态. 动量守恒定律是力学中的一个重要规律,在运用动量守恒定律解题时,常会遇到相互作用的几个物体间的临界问题,求解这类问题要注意分析临界状态,把握相关的临界条件.现把与应用动量守恒定律解题相关的临界问题做初步的分析和讨论.1.涉及弹簧的临界问题
对于由弹簧组成的系统,在物体间发生相互作用的过程中,当弹簧被压缩到最短(或拉伸到最长)时,弹簧两端的两个物体的速度必相等。
2.涉及追碰的临界问题
两个在光滑水平面上做匀速直线运动的物体,甲物体追上乙物体的条件是甲物体的速度v甲必须大于乙物体的速度v乙,即v甲>v乙,而甲物体刚好追不上乙物体的临界条件是v甲=v乙。3.涉及子弹打木块的临界问题
子弹打木块是一种常见的模型.子弹刚好击穿木块的临界条件为子弹穿出时的速度与木块的速度相同. 甲、乙两个小孩各乘一辆冰车在水平冰面上游戏,甲和他的冰车的总质量为M=30 kg,乙和他的冰车的总质量也是30 kg.甲推着一个质量m=15 kg的箱子,和他一起以大小为v0=2 m/s的速度滑行,乙以同样大小的速度迎面滑来,为了避免相碰,甲突然将箱子沿冰面推给乙,箱子滑到乙处时乙迅速把它抓住.若不计冰面的摩擦力,求甲至少要以多大的速度(相对于冰面)将箱子推出,才能避免与乙相撞?【精讲精析】 当甲把箱子推出后,甲的运动存在三种可能:①继续向前,方向不变;②停止运动;③反向运动.由动量守恒定律可知,第一种可能若能实现目标,则箱子获得的速度最小.设箱子推出后的速度为v,取甲运动方向为正方向,则对甲和箱子在推出过程中运用动量守恒定律有(M+m)v0=Mv甲+mv箱子推出后,被乙抓住,为避免甲、乙相撞,则乙必须后退,对乙和箱子运用动量守恒定律得:
mv-Mv0=(M+m)v乙
要使甲、乙不相撞,并使推出箱子的速度最小的临界条件为v甲=v乙.
解以上三式得v=5.2 m/s.
【答案】 5.2 m/s【规律总结】 在处理碰撞中动量守恒的问题时,要抓住几个关键点,一是选取动量守恒的系统,二是弄清碰撞的类型,三是碰撞过程中存在的关系:能量转化关系、几何关系、速度关系等,如本题中的速度关系就是典型问题.碰撞问题是动量与能量结合求解的典型问题.应用动量和能量观点解决问题的优点都是不必过细分析物理过程的细节,但要明确指出所研究的过程和状态. 用轻弹簧相连的质量均为2 kg的A、B两物块都以v=6 m/s的速度在光滑的水平面上运动,弹簧处于原长,质量为4 kg的物块C在前方静止,如图1-2所示.B与C碰后二者粘在一起运动.在以后的运动中,求:图1-2(1)当弹簧的弹性势能最大时,物体A的速度是多大?
(2)弹性势能最大值是多少?
(3)A的速度可能向左吗?为什么?【精讲精析】 (1)设弹性势能最大时,A的速度为v1,
当A、B、C三个物块同速时,弹性势能最大,由动量守恒定律有:
(mA+mB)v=(mA+mB+mC)v1
解得:v1=3 m/s。【答案】 (1)3 m/s (2)12 J (3)见精讲精析
【规律总结】 弹簧类问题多数要出现“压缩到最短”“拉伸到最长”“最大弹性势能”等关键词,这种情况下一般都意味着系统速度相等.要善于理解、抓住这类隐含条件.谢 谢
同课章节目录
