人教A版高中数学选修4-4第二讲第2节《圆锥曲线的参数方程》课件 (共37张PPT)
文档属性
| 名称 | 人教A版高中数学选修4-4第二讲第2节《圆锥曲线的参数方程》课件 (共37张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-22 18:44:22 | ||
图片预览








文档简介
(共37张PPT)
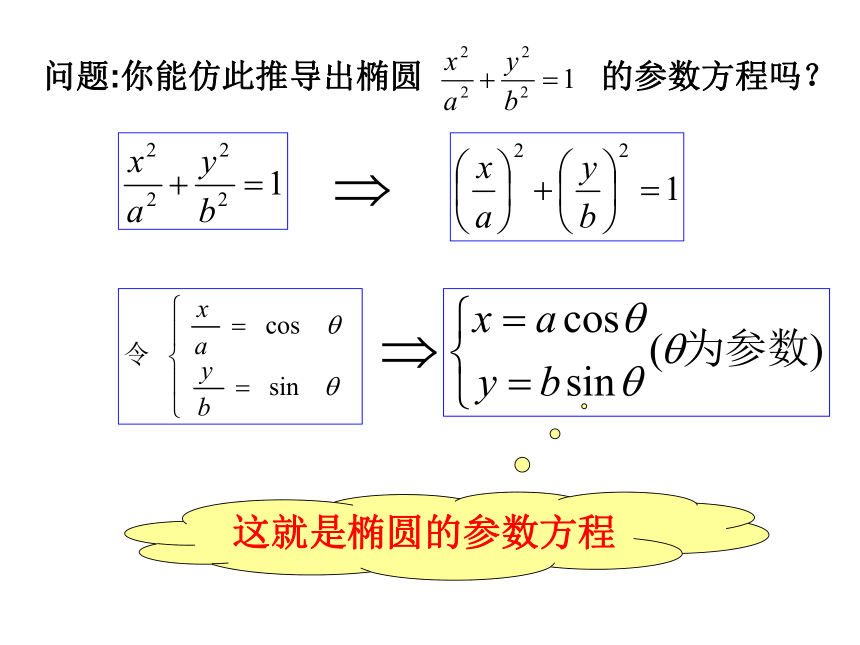
1.椭圆的参数方程
一、知识回顾
这就是椭圆的参数方程
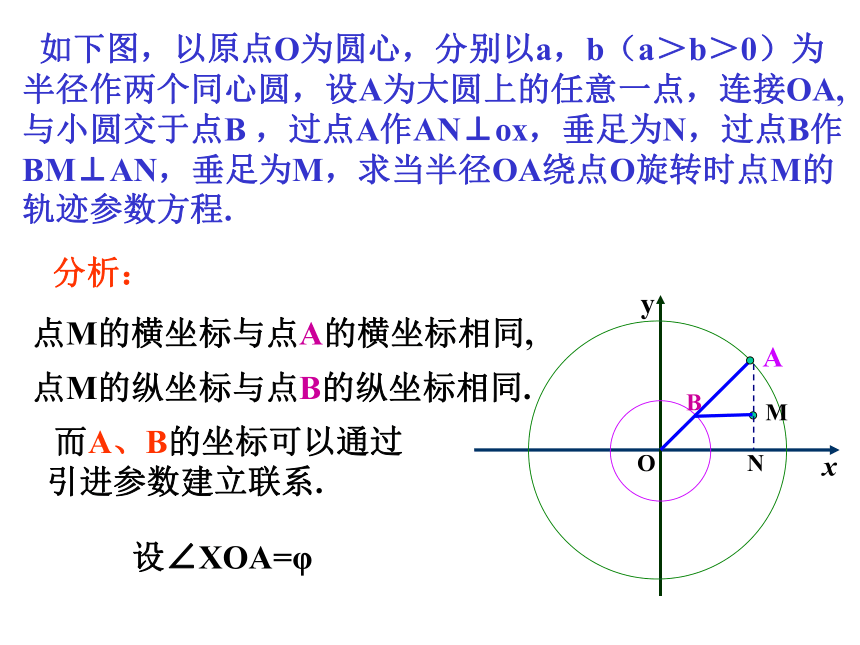
如下图,以原点O为圆心,分别以a,b(a>b>0)为半径作两个同心圆,设A为大圆上的任意一点,连接OA,与小圆交于点B ,过点A作AN⊥ox,垂足为N,过点B作BM⊥AN,垂足为M,求当半径OA绕点O旋转时点M的轨迹参数方程.
分析:
点M的横坐标与点A的横坐标相同,
点M的纵坐标与点B的纵坐标相同.
而A、B的坐标可以通过
引进参数建立联系.
设∠XOA=φ
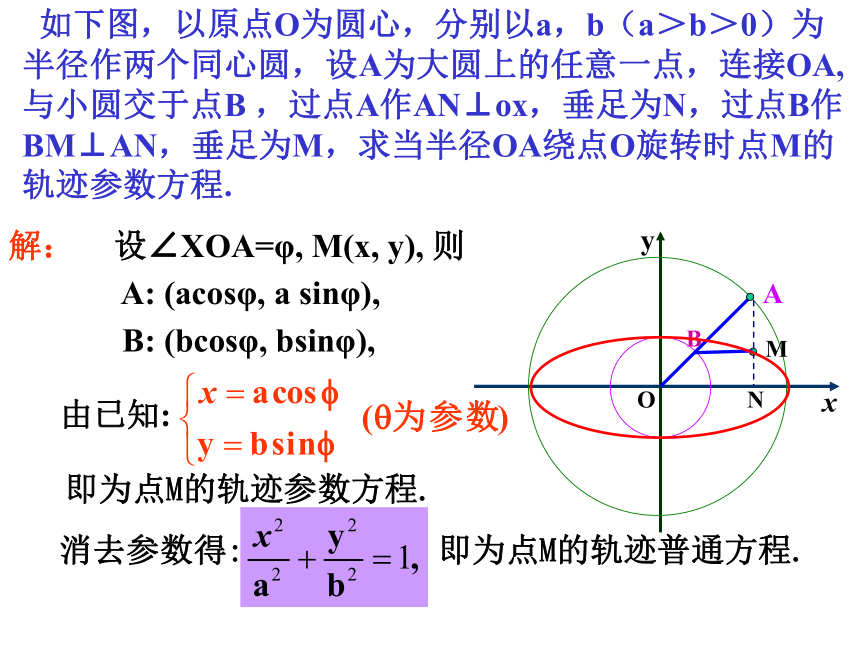
解:
设∠XOA=φ, M(x, y), 则
A: (acosφ, a sinφ),
B: (bcosφ, bsinφ),
由已知:
即为点M的轨迹参数方程.
消去参数得:
即为点M的轨迹普通方程.
如下图,以原点O为圆心,分别以a,b(a>b>0)为半径作两个同心圆,设A为大圆上的任意一点,连接OA,与小圆交于点B ,过点A作AN⊥ox,垂足为N,过点B作BM⊥AN,垂足为M,求当半径OA绕点O旋转时点M的轨迹参数方程.
2 .在椭圆的参数方程中,常数a、b分别是椭圆的长半轴长和短半轴长. a>b
知识归纳
椭圆的标准方程:
椭圆的参数方程中参数φ的几何意义:
圆的标准方程:
圆的参数方程:
x2+y2=r2
θ的几何意义是
∠AOP=θ
椭圆的参数方程:
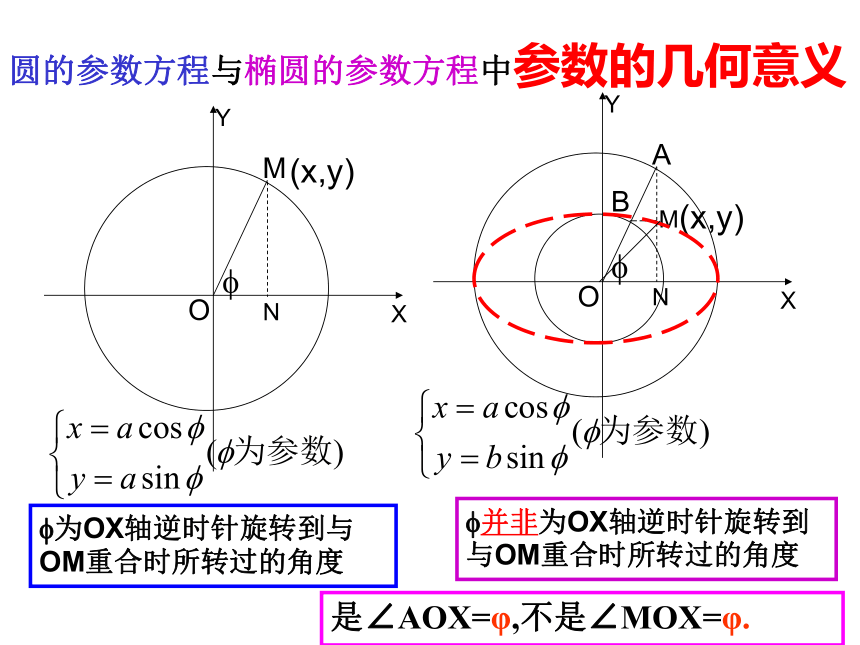
是∠AOX=φ,不是∠MOX=φ.
圆的参数方程与椭圆的参数方程中参数的几何意义
?为OX轴逆时针旋转到与OM重合时所转过的角度
?并非为OX轴逆时针旋转到与OM重合时所转过的角度
是∠AOX=φ,不是∠MOX=φ.
【练习1】把下列普通方程化为参数方程.
把下列参数方程化为普通方程
练习2:已知椭圆的参数方程为 ( 是参数) ,则此椭圆的长轴长为( ),短轴长为( ),焦点坐标是( ),离心率是( )。
4
2
例1、如图,在椭圆x2/9+y2/4=1上求一点M,使M到直线 l:x+2y-10=0的距离最小.
分析1
平移直线 l 至首次与椭圆相切,切点即为所求.
小结:借助椭圆的参数方程,可以将椭圆上的任意一点的坐标用三角函数表示,利用三角知识加以解决。
例1、如图,在椭圆x2/9+y2/4=1上求一点M,使M到直线 l:x+2y-10=0的距离最小.
分析2
例2.已知椭圆 ,求椭圆内接矩形面积的最大值.
解:设椭圆内接矩形的一个顶点坐标为
所以椭圆内接矩形面积的最大值为2ab.
例3:已知A,B两点是椭圆
与坐标轴正半轴的两个交点,在第一象限的椭圆弧上求一点P,使四边形OAPB的面积最大.
2.双曲线的参数方程
?
a
o
x
y
)
M
B
A
双曲线的参数方程
b
?
a
o
x
y
)
M
B
A
双曲线的参数方程
b
说明:
?
a
o
x
y
)
M
B
A
b
双曲线的参数方程
解:
双曲线的参数方程
注意:双曲线还有什么参数方程?
3.抛物线的参数方程
x
y
o
M(x,y)
抛物线的参数方程
B
A
M
c
练习:
练习:
练习4
2、θ取一切实数时,连接A(4sinθ,6cosθ)和B(-4cosθ,
6sinθ)两点的线段的中点轨迹是 .
A. 圆 B. 椭圆 C. 直线 D. 线段
B
设中点M (x, y)
x=2sinθ-2cosθ
y=3cosθ+3sinθ
它的焦距是多少?
B
练习5
小结
(1)椭圆的参数方程与应用
注意:椭圆参数与圆的参数方程中参数的几何意义不同。
(2)椭圆与直线相交问题
1.椭圆的参数方程
一、知识回顾
这就是椭圆的参数方程
如下图,以原点O为圆心,分别以a,b(a>b>0)为半径作两个同心圆,设A为大圆上的任意一点,连接OA,与小圆交于点B ,过点A作AN⊥ox,垂足为N,过点B作BM⊥AN,垂足为M,求当半径OA绕点O旋转时点M的轨迹参数方程.
分析:
点M的横坐标与点A的横坐标相同,
点M的纵坐标与点B的纵坐标相同.
而A、B的坐标可以通过
引进参数建立联系.
设∠XOA=φ
解:
设∠XOA=φ, M(x, y), 则
A: (acosφ, a sinφ),
B: (bcosφ, bsinφ),
由已知:
即为点M的轨迹参数方程.
消去参数得:
即为点M的轨迹普通方程.
如下图,以原点O为圆心,分别以a,b(a>b>0)为半径作两个同心圆,设A为大圆上的任意一点,连接OA,与小圆交于点B ,过点A作AN⊥ox,垂足为N,过点B作BM⊥AN,垂足为M,求当半径OA绕点O旋转时点M的轨迹参数方程.
2 .在椭圆的参数方程中,常数a、b分别是椭圆的长半轴长和短半轴长. a>b
知识归纳
椭圆的标准方程:
椭圆的参数方程中参数φ的几何意义:
圆的标准方程:
圆的参数方程:
x2+y2=r2
θ的几何意义是
∠AOP=θ
椭圆的参数方程:
是∠AOX=φ,不是∠MOX=φ.
圆的参数方程与椭圆的参数方程中参数的几何意义
?为OX轴逆时针旋转到与OM重合时所转过的角度
?并非为OX轴逆时针旋转到与OM重合时所转过的角度
是∠AOX=φ,不是∠MOX=φ.
【练习1】把下列普通方程化为参数方程.
把下列参数方程化为普通方程
练习2:已知椭圆的参数方程为 ( 是参数) ,则此椭圆的长轴长为( ),短轴长为( ),焦点坐标是( ),离心率是( )。
4
2
例1、如图,在椭圆x2/9+y2/4=1上求一点M,使M到直线 l:x+2y-10=0的距离最小.
分析1
平移直线 l 至首次与椭圆相切,切点即为所求.
小结:借助椭圆的参数方程,可以将椭圆上的任意一点的坐标用三角函数表示,利用三角知识加以解决。
例1、如图,在椭圆x2/9+y2/4=1上求一点M,使M到直线 l:x+2y-10=0的距离最小.
分析2
例2.已知椭圆 ,求椭圆内接矩形面积的最大值.
解:设椭圆内接矩形的一个顶点坐标为
所以椭圆内接矩形面积的最大值为2ab.
例3:已知A,B两点是椭圆
与坐标轴正半轴的两个交点,在第一象限的椭圆弧上求一点P,使四边形OAPB的面积最大.
2.双曲线的参数方程
?
a
o
x
y
)
M
B
A
双曲线的参数方程
b
?
a
o
x
y
)
M
B
A
双曲线的参数方程
b
说明:
?
a
o
x
y
)
M
B
A
b
双曲线的参数方程
解:
双曲线的参数方程
注意:双曲线还有什么参数方程?
3.抛物线的参数方程
x
y
o
M(x,y)
抛物线的参数方程
B
A
M
c
练习:
练习:
练习4
2、θ取一切实数时,连接A(4sinθ,6cosθ)和B(-4cosθ,
6sinθ)两点的线段的中点轨迹是 .
A. 圆 B. 椭圆 C. 直线 D. 线段
B
设中点M (x, y)
x=2sinθ-2cosθ
y=3cosθ+3sinθ
它的焦距是多少?
B
练习5
小结
(1)椭圆的参数方程与应用
注意:椭圆参数与圆的参数方程中参数的几何意义不同。
(2)椭圆与直线相交问题
