北师大版高中数学必修3第二章算法初步第二节算法框图的基本结构及设计2.2变量与赋值教学课件(共20张PPT)
文档属性
| 名称 | 北师大版高中数学必修3第二章算法初步第二节算法框图的基本结构及设计2.2变量与赋值教学课件(共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-22 18:49:13 | ||
图片预览







文档简介
(共20张PPT)
变量与赋值
i=2
输入n
示意图
顺序结构在程序框图中的体现就是用流程线将程序框自上而下地连接起来,按顺序执行算法步骤。如在示意图中,A框和B框是依次执行的,只有在执行完A框指定的操作后,才能接着执行B框所指定的操作。
选择结构是指在算法中通过对条件的判断,根据条件是否成立而选择不同流向的算法结构.
示意图
变量和函数是中学数学里最重要和最基本的概念.
在算法和程序设计中,它们仍然发挥着重要和基本的作用,它们会使算法的表述变得非常简洁、清楚.
变量
在研究问题的过程中可以取不同数值的量称为变量。
解:
例 设计一种算法,从5个实数中找出最大数,并用流程图表示.
设这5个数分别为:a1,a2,a3,a4,a5
1、将a1与a2比较,将较大的数记作b.
2、再将b与a3比较,将较大的数记作b.
3、再将b与a4比较,将较大的数记作b.
4、再将b与a5比较,将较大的数记作b.
5、输出b,b的值即为所求的最大数
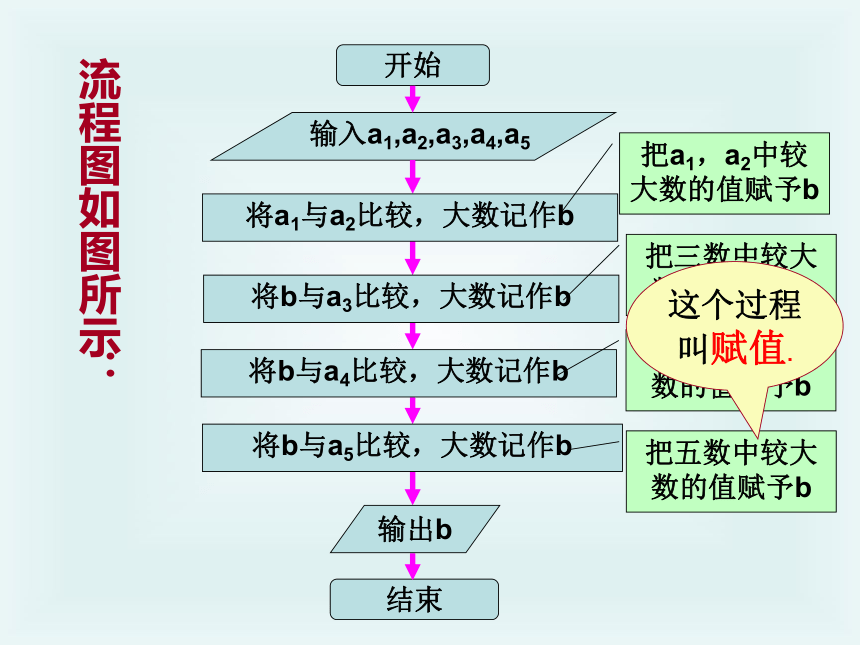
流程图如图所示:
开始
输入a1,a2,a3,a4,a5
结束
将a1与a2比较,大数记作b
将b与a3比较,大数记作b
将b与a4比较,大数记作b
将b与a5比较,大数记作b
输出b
把a1,a2中较大数的值赋予b
把三数中较大数的值赋予b
把四数中较大数的值赋予b
把五数中较大数的值赋予b
这个过程叫赋值.
变量名=表达式
1.在上例中每一步都要与上一步中的大数b比较,在将大数的值重新记作b,通常叫b为变量,这种将大数重新记作b的过程,我们叫赋值给b.
2.赋值语句的一般格式为:
例如: x=4
y=6
3.变量和赋值是算法的基本概念,变量就像一个盒子,赋值就像给盒子里放东西,但是每次只能装一个“数值”,放入新的数值后,原来的数值就被新的数值所取代。
开始
输入a1,a2,a3,a4,a5
b=a1
b否
是
b=a2
输出b
结束
b否
是
b=a3
b否
是
b=a4
b否
是
b=a5
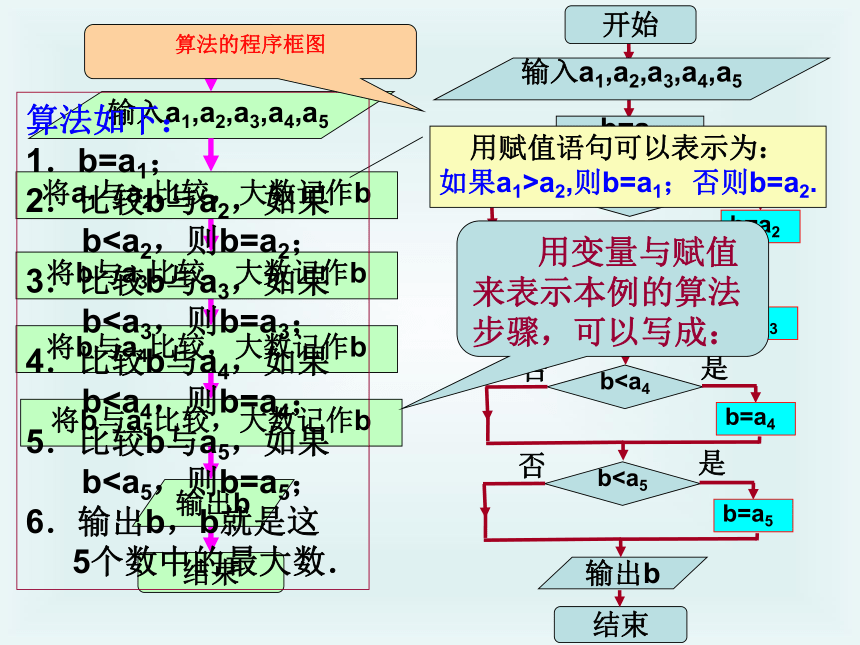
用赋值语句可以表示为:
如果a1>a2,则b=a1;否则b=a2.
用变量与赋值来表示本例的算法步骤,可以写成:
算法如下:
1.b=a1;
2.比较b与a2,如果
b3.比较b与a3,如果
b4.比较b与a4,如果
b5.比较b与a5,如果
b6.输出b,b就是这
5个数中的最大数.
算法的程序框图
注意:⑴赋值号左边只能是变量名字,而不是表达式。
问题1:
问题2:在数学中x=y与y=x的意义是一样的,那么在赋值语句中一样吗?
注意:⑵赋值号左右不能对换。赋值语句是将赋值号右边的表达式的值赋给赋值号左边的变量。
赋值号与数学中的等号意义不同:
Y=X,表示用X的值替代变量Y原先的取值。
X=Y,表示用Y的值替代变量X原先的取值。
故“Y=X与 X=Y”的含义运行结果是不同的。
注意:⑶不能利用赋值语句进行代数的演算(如化简、因式分解、解方程等)
例如:①x2+10x+16=0
(x+8)(x+2)=0
X=-8,x=-2
②y=x2-1=(x-1)(x+1)
这是不能实现的
问题3:我们知道a=a+1在数学中是不成立的,但在赋值语句中a=a+1成立吗?为什么?
答: 在赋值语句中是成立的,意思是将a的原值加1在赋给a,即a的值增加1。如果多次给一个变量赋值,则该变量的值取最后赋予的那个值。
思考: 下列程序运行后,结果分别是什么?
(1) a=1;
b=2a+1;
输出b
(2) i=2;
i=3i+1;
输出i
(3) i=1;
s=i;
i=i+3;
s=2s+3i;
输出s,i
(4) a=3;
b=-5;
c=8;
a=b;
b=c;
输出a,b,c
(5) a=3;
b=-5;
c=8;
a=b;
b=c;
c= a;
输出a,b,c
b=3
i=7
s=14,i=4
a=-5,b=8,c=8
a=-5,
b=8,
c=-5
问题4:如何交换两个变量x和y?
思考:现有两个粉笔盒,一个装满白色粉笔,一个装满红色粉笔,如何交换两个盒子所装的铅笔?
桥梁:空盒子
桥梁:中间变量
活动探究
已知 两个数 a 和 b , 设计一个算法使a 和 b 位置互换。
a
b
S
a
算法如下:
a
(a)
(b)
(1)S = a
(2)a = b
(3)b = S
(4)输出结果a,b.
练习.写出求1×2×3×4×5的一个算法.
开始
结束
输出S
S=1
S=2S
S=3S
S=4S
S=5S
金融作为现代生活中不可或缺的行业,与我们有着密切的关系,某人现有5000元人民币,他按照定期一年存款方式存入银行,到期自动转存,按复利计算,已知当前定期一年的利率为2.25%,试求5年后这个人连本带息可以取出多少钱?实际算法解决问题,画出流程图。
分析:设某年后可以支取p元,算法如下:
n年后本利和为:
p=5000(1+2.25%)n
解
设某年后可以支取p元,算法如下:
(1)一年后:p=5000(1+2.25%);
(2)二年后:
p=5000(1+2.25%)(1+2.25%)
(3)三年后:
p=5000(1+2.25%) ·
(1+2.25%)(1+2.25%)
(4)四年后:
p=5000(1+2.25%)(1+2.25%)
· (1+2.25%)(1+2.25%)
(5)五年后:
p=5000(1+2.25%)(1+2.25%) ·
(1+2.25%)(1+2.25%)(1+2.25%)
(6)输出p
开始
p=5000
p=p(1+2.25%)
p=p(1+2.25%)
p=p(1+2.25%)
p=p(1+2.25%)
p=p(1+2.25%)
输出p
结束
1.变量与赋值的概念
2.变量和赋值是算法中十分重要的概念,掌握将常数赋予变量,将其他变量的表达式赋予变量,将含有自身变量的表达式赋予变量,理解这些赋值方式的意义,切实学会通过赋值的方式改变变量的值,学会给变量赋值是构造算法的关键,也是算法的基本要求.
变量与赋值
i=2
输入n
示意图
顺序结构在程序框图中的体现就是用流程线将程序框自上而下地连接起来,按顺序执行算法步骤。如在示意图中,A框和B框是依次执行的,只有在执行完A框指定的操作后,才能接着执行B框所指定的操作。
选择结构是指在算法中通过对条件的判断,根据条件是否成立而选择不同流向的算法结构.
示意图
变量和函数是中学数学里最重要和最基本的概念.
在算法和程序设计中,它们仍然发挥着重要和基本的作用,它们会使算法的表述变得非常简洁、清楚.
变量
在研究问题的过程中可以取不同数值的量称为变量。
解:
例 设计一种算法,从5个实数中找出最大数,并用流程图表示.
设这5个数分别为:a1,a2,a3,a4,a5
1、将a1与a2比较,将较大的数记作b.
2、再将b与a3比较,将较大的数记作b.
3、再将b与a4比较,将较大的数记作b.
4、再将b与a5比较,将较大的数记作b.
5、输出b,b的值即为所求的最大数
流程图如图所示:
开始
输入a1,a2,a3,a4,a5
结束
将a1与a2比较,大数记作b
将b与a3比较,大数记作b
将b与a4比较,大数记作b
将b与a5比较,大数记作b
输出b
把a1,a2中较大数的值赋予b
把三数中较大数的值赋予b
把四数中较大数的值赋予b
把五数中较大数的值赋予b
这个过程叫赋值.
变量名=表达式
1.在上例中每一步都要与上一步中的大数b比较,在将大数的值重新记作b,通常叫b为变量,这种将大数重新记作b的过程,我们叫赋值给b.
2.赋值语句的一般格式为:
例如: x=4
y=6
3.变量和赋值是算法的基本概念,变量就像一个盒子,赋值就像给盒子里放东西,但是每次只能装一个“数值”,放入新的数值后,原来的数值就被新的数值所取代。
开始
输入a1,a2,a3,a4,a5
b=a1
b
是
b=a2
输出b
结束
b
是
b=a3
b
是
b=a4
b
是
b=a5
用赋值语句可以表示为:
如果a1>a2,则b=a1;否则b=a2.
用变量与赋值来表示本例的算法步骤,可以写成:
算法如下:
1.b=a1;
2.比较b与a2,如果
b
b
b
b
5个数中的最大数.
算法的程序框图
注意:⑴赋值号左边只能是变量名字,而不是表达式。
问题1:
问题2:在数学中x=y与y=x的意义是一样的,那么在赋值语句中一样吗?
注意:⑵赋值号左右不能对换。赋值语句是将赋值号右边的表达式的值赋给赋值号左边的变量。
赋值号与数学中的等号意义不同:
Y=X,表示用X的值替代变量Y原先的取值。
X=Y,表示用Y的值替代变量X原先的取值。
故“Y=X与 X=Y”的含义运行结果是不同的。
注意:⑶不能利用赋值语句进行代数的演算(如化简、因式分解、解方程等)
例如:①x2+10x+16=0
(x+8)(x+2)=0
X=-8,x=-2
②y=x2-1=(x-1)(x+1)
这是不能实现的
问题3:我们知道a=a+1在数学中是不成立的,但在赋值语句中a=a+1成立吗?为什么?
答: 在赋值语句中是成立的,意思是将a的原值加1在赋给a,即a的值增加1。如果多次给一个变量赋值,则该变量的值取最后赋予的那个值。
思考: 下列程序运行后,结果分别是什么?
(1) a=1;
b=2a+1;
输出b
(2) i=2;
i=3i+1;
输出i
(3) i=1;
s=i;
i=i+3;
s=2s+3i;
输出s,i
(4) a=3;
b=-5;
c=8;
a=b;
b=c;
输出a,b,c
(5) a=3;
b=-5;
c=8;
a=b;
b=c;
c= a;
输出a,b,c
b=3
i=7
s=14,i=4
a=-5,b=8,c=8
a=-5,
b=8,
c=-5
问题4:如何交换两个变量x和y?
思考:现有两个粉笔盒,一个装满白色粉笔,一个装满红色粉笔,如何交换两个盒子所装的铅笔?
桥梁:空盒子
桥梁:中间变量
活动探究
已知 两个数 a 和 b , 设计一个算法使a 和 b 位置互换。
a
b
S
a
算法如下:
a
(a)
(b)
(1)S = a
(2)a = b
(3)b = S
(4)输出结果a,b.
练习.写出求1×2×3×4×5的一个算法.
开始
结束
输出S
S=1
S=2S
S=3S
S=4S
S=5S
金融作为现代生活中不可或缺的行业,与我们有着密切的关系,某人现有5000元人民币,他按照定期一年存款方式存入银行,到期自动转存,按复利计算,已知当前定期一年的利率为2.25%,试求5年后这个人连本带息可以取出多少钱?实际算法解决问题,画出流程图。
分析:设某年后可以支取p元,算法如下:
n年后本利和为:
p=5000(1+2.25%)n
解
设某年后可以支取p元,算法如下:
(1)一年后:p=5000(1+2.25%);
(2)二年后:
p=5000(1+2.25%)(1+2.25%)
(3)三年后:
p=5000(1+2.25%) ·
(1+2.25%)(1+2.25%)
(4)四年后:
p=5000(1+2.25%)(1+2.25%)
· (1+2.25%)(1+2.25%)
(5)五年后:
p=5000(1+2.25%)(1+2.25%) ·
(1+2.25%)(1+2.25%)(1+2.25%)
(6)输出p
开始
p=5000
p=p(1+2.25%)
p=p(1+2.25%)
p=p(1+2.25%)
p=p(1+2.25%)
p=p(1+2.25%)
输出p
结束
1.变量与赋值的概念
2.变量和赋值是算法中十分重要的概念,掌握将常数赋予变量,将其他变量的表达式赋予变量,将含有自身变量的表达式赋予变量,理解这些赋值方式的意义,切实学会通过赋值的方式改变变量的值,学会给变量赋值是构造算法的关键,也是算法的基本要求.
