人教A版选修4-4第二讲2.1曲线的参数方程(共29张PPT)
文档属性
| 名称 | 人教A版选修4-4第二讲2.1曲线的参数方程(共29张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 977.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-22 18:46:38 | ||
图片预览







文档简介
(共29张PPT)
第二讲 参数方程
1.参数方程的概念
【教学目标】
1、弄清曲线参数方程的概念,能选取适当的参数,求简单曲线的参数方程 。掌握参数方程化为普通方程几种基本方法,选取适当的参数化普通方程为参数方程
2、会解决简单证明问题,能灵活选取适当的参数化普通方程为参数方程,培养学生的逻辑推理能力和思维能力。
3、通过学生的参与过程,培养他们手脑并用、多思勤练的良好学习习惯和勇于探索、锲而不舍的治学精神。
【重点与难点】
重点:曲线参数方程的定义及方法,参数方程与普通方程的等价性。
难点:曲线参数方程的定义及方法,参数方程与普通方程的等价性。
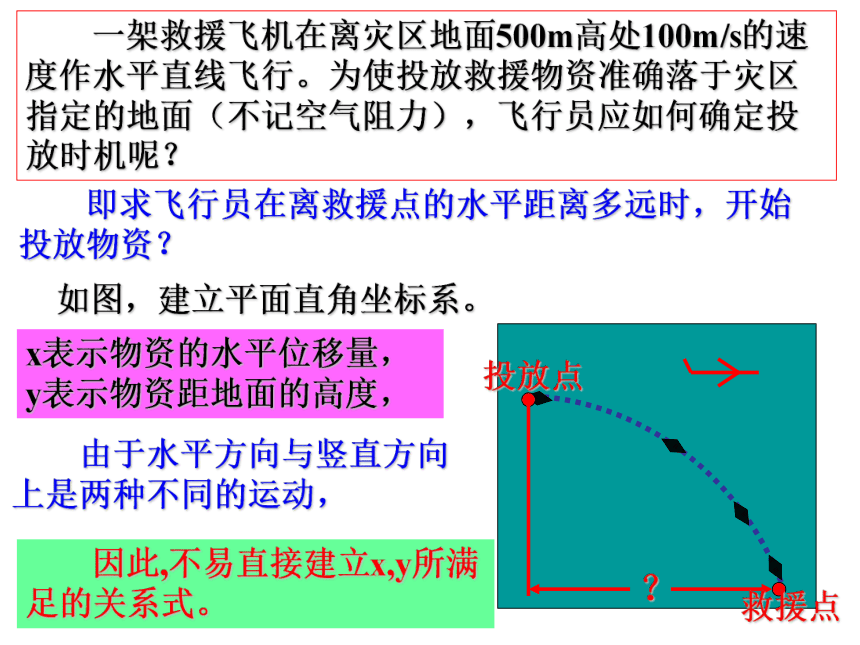
一架救援飞机在离灾区地面500m高处100m/s的速度作水平直线飞行。为使投放救援物资准确落于灾区指定的地面(不记空气阻力),飞行员应如何确定投放时机呢?
即求飞行员在离救援点的水平距离多远时,开始投放物资?
如图,建立平面直角坐标系。
因此,不易直接建立x,y所满足的关系式。
x表示物资的水平位移量,
y表示物资距地面的高度,
由于水平方向与竖直方向上是两种不同的运动,
物资投出机舱后,它的运动由下列两种运动合成:
(1)沿ox作初速为100m/s的匀速直线运动;
(2)沿oy反方向作自由落体运动。
在这个运动中涉及到哪几个变量?这些变量之间有什么关系?
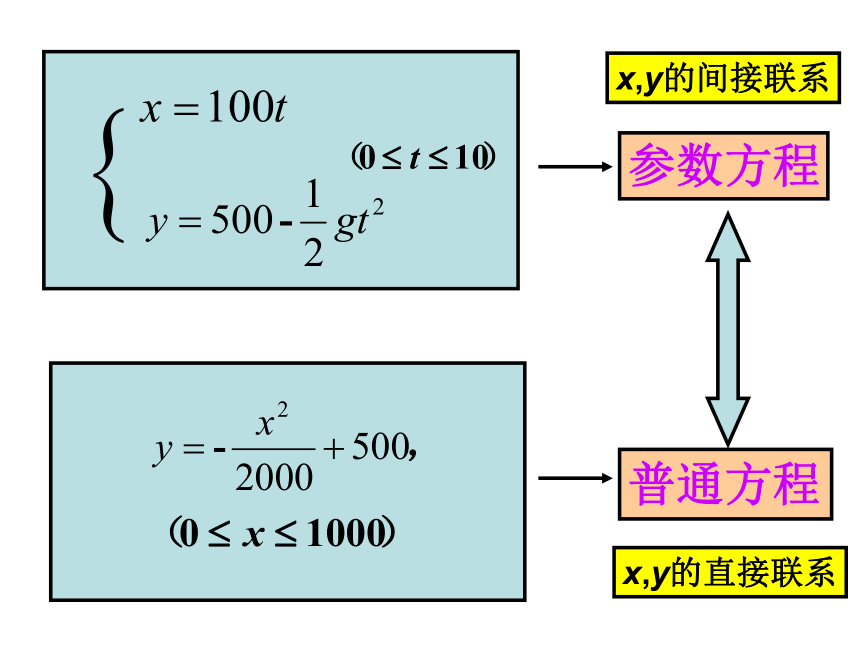
t时刻,水平位移为x=100t,离地面高度y,即:
y=500-gt2/2,
物资落地时,应有y=0,
得x≈10.10m;
即500-gt2/2=0,解得,t≈10.10s,
因此飞行员在距离救援点水平距离约为1010米时投放物资,可以使其准确落在指定位置。
参数方程的概念
一般地,在平面直角坐标系中,如果曲线C上任意一点P的坐标x,y都可以表示为某个变量t的函数
反过来,对于t的每一个允许值,由函数式 所确定的点P(x,y)都在曲线C上,
那么方程 叫做曲线C的参数方程,变量t是参变数,简称参数。
参数方程
普通方程
x,y的间接联系
x,y的直接联系
解:(1)把点M1的坐标(0,1)代入方程组,解得t=0,所以M1在曲线上.
这个方程无解,所以点M2不在曲线C上.
解得t=2, a=9 所以,a=9.
B
A(1,4); B (25/16, 0) C(1, -3) D(±25/16, 0)
D
A(2,7); B(1/3, 2/3) C(1/2, 1/2) D(1,0)
(1)由题意可知: 1+2t=5,at2=4;a=1,t=2;
代入第二个方程得: y=(x-1)2/4
4 动点M作等速直线运动, 它在x轴和y轴方向的速度分别为5和12 , 运动开始时位于点P(1,2), 求点M的轨迹参数方程.
解:设动点M (x,y) 运动时间为t,依题意,得
A 一个定点 B 一个椭圆
C 一条抛物线 D 一条直线
D
圆的参数方程
M(x, y)
圆周运动中,当物体绕定轴作匀速运动时,物体上的各个点都作匀速圆周运动,
怎样刻画运动中点的位置呢?
那么θ=ωt. 设|OM|=r,那么由三角函数定义,有
如果在时刻t,点M转过的角度是θ,坐标是M(x, y),
这就是圆心在原点O,半径为r 的圆的参数方程
参数 t 有物理意义(质点作匀速圆周运动的时刻)
考虑到θ=ωt,也可以取θ为参数,于是有
圆心为原点半径为r 的圆的参数方程.
其中参数θ的几何意义是OM0绕点O逆时针旋转到OM的位置时,OM0转过的角度
一般地,同一条曲线,可以选取不同的变数为参数,
另外,要注明参数及参数的取值范围。
解: x2+y2+2x-6y+9=0化为标准方程,为
(x+1)2+(y-3)2=1
∴参数方程为
(θ为参数)
例1 已知圆方程x2+y2+2x-6y+9=0,将它化为参数方程。
例2 如图,圆O的半径为2,P是圆上的动点,Q(6,0)是x轴上的定点,M是PQ的中点,当点P绕O作匀速圆周运动时,求点M的轨迹的参数方程。
解:设点M的坐标是(x, y),
则点P的坐标是(2cosθ,2sinθ).
由中点坐标公式可得
因此,点M的轨迹的参数方程是
练习
A
A.36 B.6 C.26 D.25
D
A
.
则点P的坐标是(4cosθ,4sinθ).
∵2|PM|=|MA|, ∴由题设
∴(x-12, y)=
因此,点M的轨迹的参数方程是
参数方程和
普通方程的互化
例1、把下列参数方程化为普通方程,并说明它们各表示什么曲线?
这是以(1,1)为端点的一条射线;
步骤:
(1)消参; (2)求定义域。
练习、将下列参数方程化为普通方程:
(1)(x-2)2+y2=9
(2)y=1- 2x2(- 1≤x≤1)
(3)x2- y=2(x≥2或x≤- 2)
注意:在参数方程与普通方程的互化中,必须使x,y的取值范围保持一致。否则,互化就是不等价的.
为什么两个参数方程合起来才是椭圆的参数方程?
解:
x,y范围与y=x2中x,y的范围相同,
代入y=x2后满足该方程,
1、曲线y=x2的一种参数方程是( ).
在y=x2中,x∈R, y≥0,
分析:
因而与 y=x2不等价;
在A、B、C中,x,y的范围都发生了变化,
而在D中,
且以
练习:
D
从而D是曲线y=x2的一种参数方程.
2、求参数方程
表示
( )
B
分析
一般思路是:化参数方程为普通方程
求出范围、判断。
解
?x2=
=1+sin?=2y,
?普通方程是x2=2y,为抛物线。
?
又0?0故应选 (B)
说明:
这里切不可轻易去绝对值讨论,平方法是最好的方法。
练习 把下列普通方程化为参数方程:
练习 把下列参数方程化为普通方程
小结
1. 参数方程的概念;
2. 圆的参数方程;
3. 参数方程与普通方程的互化.
第二讲 参数方程
1.参数方程的概念
【教学目标】
1、弄清曲线参数方程的概念,能选取适当的参数,求简单曲线的参数方程 。掌握参数方程化为普通方程几种基本方法,选取适当的参数化普通方程为参数方程
2、会解决简单证明问题,能灵活选取适当的参数化普通方程为参数方程,培养学生的逻辑推理能力和思维能力。
3、通过学生的参与过程,培养他们手脑并用、多思勤练的良好学习习惯和勇于探索、锲而不舍的治学精神。
【重点与难点】
重点:曲线参数方程的定义及方法,参数方程与普通方程的等价性。
难点:曲线参数方程的定义及方法,参数方程与普通方程的等价性。
一架救援飞机在离灾区地面500m高处100m/s的速度作水平直线飞行。为使投放救援物资准确落于灾区指定的地面(不记空气阻力),飞行员应如何确定投放时机呢?
即求飞行员在离救援点的水平距离多远时,开始投放物资?
如图,建立平面直角坐标系。
因此,不易直接建立x,y所满足的关系式。
x表示物资的水平位移量,
y表示物资距地面的高度,
由于水平方向与竖直方向上是两种不同的运动,
物资投出机舱后,它的运动由下列两种运动合成:
(1)沿ox作初速为100m/s的匀速直线运动;
(2)沿oy反方向作自由落体运动。
在这个运动中涉及到哪几个变量?这些变量之间有什么关系?
t时刻,水平位移为x=100t,离地面高度y,即:
y=500-gt2/2,
物资落地时,应有y=0,
得x≈10.10m;
即500-gt2/2=0,解得,t≈10.10s,
因此飞行员在距离救援点水平距离约为1010米时投放物资,可以使其准确落在指定位置。
参数方程的概念
一般地,在平面直角坐标系中,如果曲线C上任意一点P的坐标x,y都可以表示为某个变量t的函数
反过来,对于t的每一个允许值,由函数式 所确定的点P(x,y)都在曲线C上,
那么方程 叫做曲线C的参数方程,变量t是参变数,简称参数。
参数方程
普通方程
x,y的间接联系
x,y的直接联系
解:(1)把点M1的坐标(0,1)代入方程组,解得t=0,所以M1在曲线上.
这个方程无解,所以点M2不在曲线C上.
解得t=2, a=9 所以,a=9.
B
A(1,4); B (25/16, 0) C(1, -3) D(±25/16, 0)
D
A(2,7); B(1/3, 2/3) C(1/2, 1/2) D(1,0)
(1)由题意可知: 1+2t=5,at2=4;a=1,t=2;
代入第二个方程得: y=(x-1)2/4
4 动点M作等速直线运动, 它在x轴和y轴方向的速度分别为5和12 , 运动开始时位于点P(1,2), 求点M的轨迹参数方程.
解:设动点M (x,y) 运动时间为t,依题意,得
A 一个定点 B 一个椭圆
C 一条抛物线 D 一条直线
D
圆的参数方程
M(x, y)
圆周运动中,当物体绕定轴作匀速运动时,物体上的各个点都作匀速圆周运动,
怎样刻画运动中点的位置呢?
那么θ=ωt. 设|OM|=r,那么由三角函数定义,有
如果在时刻t,点M转过的角度是θ,坐标是M(x, y),
这就是圆心在原点O,半径为r 的圆的参数方程
参数 t 有物理意义(质点作匀速圆周运动的时刻)
考虑到θ=ωt,也可以取θ为参数,于是有
圆心为原点半径为r 的圆的参数方程.
其中参数θ的几何意义是OM0绕点O逆时针旋转到OM的位置时,OM0转过的角度
一般地,同一条曲线,可以选取不同的变数为参数,
另外,要注明参数及参数的取值范围。
解: x2+y2+2x-6y+9=0化为标准方程,为
(x+1)2+(y-3)2=1
∴参数方程为
(θ为参数)
例1 已知圆方程x2+y2+2x-6y+9=0,将它化为参数方程。
例2 如图,圆O的半径为2,P是圆上的动点,Q(6,0)是x轴上的定点,M是PQ的中点,当点P绕O作匀速圆周运动时,求点M的轨迹的参数方程。
解:设点M的坐标是(x, y),
则点P的坐标是(2cosθ,2sinθ).
由中点坐标公式可得
因此,点M的轨迹的参数方程是
练习
A
A.36 B.6 C.26 D.25
D
A
.
则点P的坐标是(4cosθ,4sinθ).
∵2|PM|=|MA|, ∴由题设
∴(x-12, y)=
因此,点M的轨迹的参数方程是
参数方程和
普通方程的互化
例1、把下列参数方程化为普通方程,并说明它们各表示什么曲线?
这是以(1,1)为端点的一条射线;
步骤:
(1)消参; (2)求定义域。
练习、将下列参数方程化为普通方程:
(1)(x-2)2+y2=9
(2)y=1- 2x2(- 1≤x≤1)
(3)x2- y=2(x≥2或x≤- 2)
注意:在参数方程与普通方程的互化中,必须使x,y的取值范围保持一致。否则,互化就是不等价的.
为什么两个参数方程合起来才是椭圆的参数方程?
解:
x,y范围与y=x2中x,y的范围相同,
代入y=x2后满足该方程,
1、曲线y=x2的一种参数方程是( ).
在y=x2中,x∈R, y≥0,
分析:
因而与 y=x2不等价;
在A、B、C中,x,y的范围都发生了变化,
而在D中,
且以
练习:
D
从而D是曲线y=x2的一种参数方程.
2、求参数方程
表示
( )
B
分析
一般思路是:化参数方程为普通方程
求出范围、判断。
解
?x2=
=1+sin?=2y,
?普通方程是x2=2y,为抛物线。
?
又0?0
说明:
这里切不可轻易去绝对值讨论,平方法是最好的方法。
练习 把下列普通方程化为参数方程:
练习 把下列参数方程化为普通方程
小结
1. 参数方程的概念;
2. 圆的参数方程;
3. 参数方程与普通方程的互化.
