上海市2019-2020学年度高二数学第二学期抛物线标准方程典例分析学案
文档属性
| 名称 | 上海市2019-2020学年度高二数学第二学期抛物线标准方程典例分析学案 |
|
|
| 格式 | zip | ||
| 文件大小 | 734.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-22 18:45:48 | ||
图片预览





文档简介
上海市2019-2020高二数学第二学期精品讲义
抛物线标准方程典例分析
【知识梳理】
1、抛物线的定义:平面内与一个定点F和一条定直线L的距离相等的点的轨迹叫做抛物线。
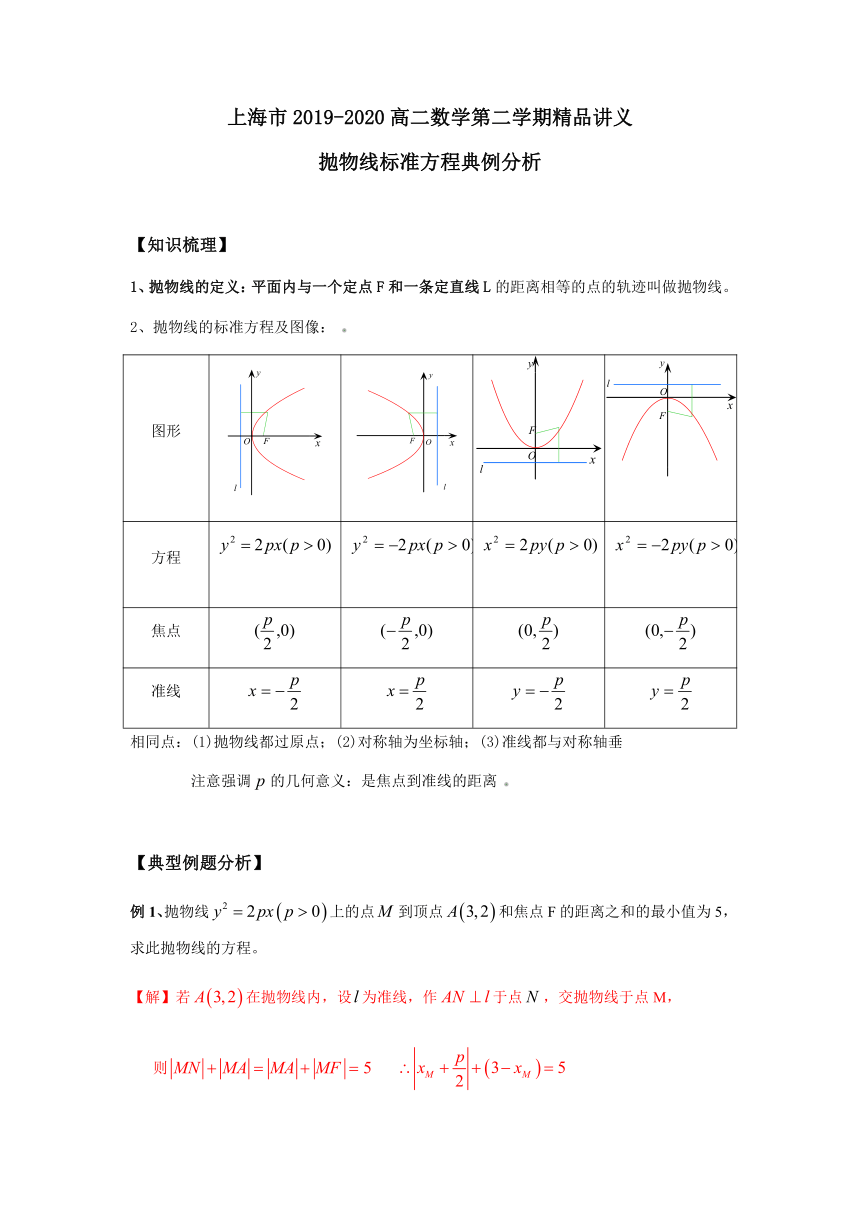
2、抛物线的标准方程及图像:
图形
方程
焦点
准线
相同点:(1)抛物线都过原点;(2)对称轴为坐标轴;(3)准线都与对称轴垂
注意强调的几何意义:是焦点到准线的距离
【典型例题分析】
例1、抛物线上的点到顶点和焦点F的距离之和的最小值为5,求此抛物线的方程。
【解】若在抛物线内,设为准线,作于点,交抛物线于点M,
则
所以
若在抛物线外,连接交抛物线于点M,则
又在抛物线外,
所以不合题意
综上,,所求抛物线方程为:
例2、定长为4的线段的端点在抛物线上移动且所在直线过焦点,求中点到轴距离的最小值,并求此时中点的坐标。
【解】设直线的方程为,代入中,整理得
因此,点到轴的距离的最小值是
例3、某抛物线形拱桥跨度是20,拱高4,在建桥时,每隔4需用一支柱支撑,求其中最长的支柱的长。
【解】以拱点为原点,水平线为轴,建立坐标系,有题意得坐标分别是
设抛物线方程为,将点的坐标代入,得
于是抛物线方程为
是的五等分点,,可得
因此最长的支柱应为3.84
例4、已知抛物线的焦点是坐标原点,则以抛物线与两坐标的三个交点为顶点的三角形面积为_________
【分析】把抛物线方程改写为得顶点,又因为原点为焦点
抛物线与轴交于
所以所求面积为
例5、已知抛物线的对称轴为轴,顶点在原点,焦点在直线,则此抛物线的方程是 ( )
A B C D
【分析】由题意知抛物线方程是标准形式,且焦点在轴上,在直线中,令 所以焦点坐标,所以抛物线方程为,选C
例6、直线过点,并且与抛物线只有一个公共点,求直线的方程。
【解】只有一个公共点有两种情况:
(1)当直线的斜率不存在时,,此时直线与抛物线相交,仅且只有一个公共点,成立;
(2)当只想斜率存在,则设联立得:
仅有一个交点,则:
所以,直线
综上,满足题意的直线为或
例7、一条隧道的横断面由抛物线弧及一个矩形的三边围成,一辆卡车空车时能通过此隧道,现载一集装箱,箱宽3,假设车与箱共高4.5,此车能否通过隧道?并说明理由。
【解】先建立直角坐标系,如图则
设抛物线方程为,将点坐标代入,得
因为车与箱共高4.5
所以集装箱上表面距抛物线型隧道拱顶0.5
设抛物线上点
代入求的
故此车不能通过隧道。
变式练习:学校科技小组在计算机上模拟航天器变轨返回试验,设计方案如图所示,航天器运行(按顺时针方向)的轨迹方程是,变轨(即航天器运行轨迹由椭圆变为抛物线)后返回的轨迹是以轴为对称轴,为顶点的抛物线的实线部分,降落点为,观测点为同时跟踪航天器。
(1)求航天器变轨后的运行轨迹所在的曲线方程;
(2)试问:当航天器在轴上方时,观测点测得离航天器的距离分别为多少时,应向航天器发出变轨指令?
【解】(1)设曲线方程为
由题意知,
所以曲线方程为
(2)设变轨点为,根据题意可知,
整理得,(舍去)
所以
(不合题意,舍去)
故当观测点测得离航天器的距离分别为,4时,
应向航天器发出变轨指令
【课堂小练】
1.以双曲线的中心为顶点,右焦点为焦点的抛物线方程为_________________
2.若抛物线C的顶点为坐标原点,焦点在坐标轴上,且经过点,则C的准线方程是___________________
3.若直线与抛物线交于两点,则线段的中点坐标是_________
4.过点且与抛物线只有一个交点的直线方程是___________________
5.对抛物线,下列说法正确的是 ( )
A 若,焦点为;若,焦点为
B若,焦点为;若,焦点为
C 不论还是,焦点都是
D不论还是,焦点都是
6.抛物线的准线方程是 ( )
A B C D
7.抛物线关于直线对称的曲线的方程是 ( )
A B C D
8.抛物线的焦点到准线的距离为 ( )
A 5 B C D
9.过点且与抛物线只有一个公共点的直线有 ( )
A 一条 B 两条 C 三条 D 由的值决定
10.过抛物线的焦点作倾斜角为的直线叫抛物线于,求的长。
11.抛物线的顶点在原点,对称轴与坐标轴重合,过两点,求抛物线方程。
12.已知顶点在原点,焦点在轴上的抛物线倍直线所截得的弦长为,求此抛物线的方程。
13.已知过抛物线的焦点F的直线与抛物线交于点A、B,求证:
答案:1. 2. 3. 4.
5.C 6.B 7. C 8.B 9.C 10. 11.
12. 13.略
【课后练习】
1.曲线的焦点坐标为_______
2.到点及到直线的距离相等的动点的轨迹方程为__________________
3.经过点的抛物线的标准方程为_________________
4.若点到抛物线的焦点的距离为5,则___________
5.到平面上的定点A和到直线距离相等的点的轨迹为 ( )
A 直线 B 抛物线 C 双曲线 D 椭圆
6.抛物线的准线方程为 ( )
A B C D
7.抛物线的焦点坐标为 ( )
A B C D
8.动圆M经过点,且与直线相切,则动圆圆心M的轨迹方程是 ( )
A B C D
9.若抛物线的焦点与椭圆的右焦点重合,则的值为 ( )
A B 2 C D 4
10.求满足下列条件的抛物线的标准方程:
(1)过点;
(2)焦点在直线
11.已知动圆M与圆外切,且与轴相切,求动圆圆心M的轨迹方程。
12.抛物线有一内接直角三角形,直角的顶点在原点,一直角边所在的直线的方程是,斜边长是,求此抛物线方程。
13.在抛物线上求一点P,使点P到焦点F与到点的距离之和最小。
答案:1. 2. 3. 4.
5.A 6.C 7.D 8.A 9.D
10.(1)
(2)
11. 12. 13.
