2020春华师大版九下数学27.3第1课时弧长与扇形的面积同步课堂练(学生版+教师版)
文档属性
| 名称 | 2020春华师大版九下数学27.3第1课时弧长与扇形的面积同步课堂练(学生版+教师版) |

|
|
| 格式 | zip | ||
| 文件大小 | 275.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-20 00:00:00 | ||
图片预览

文档简介
2020春华师大版九下数学27.3第1课时弧长与扇形的面积同步课堂练习(学生版)
基础题
知识点1 弧长的计算
1.若扇形的圆心角为90°,半径为6,则该扇形的弧长为( )
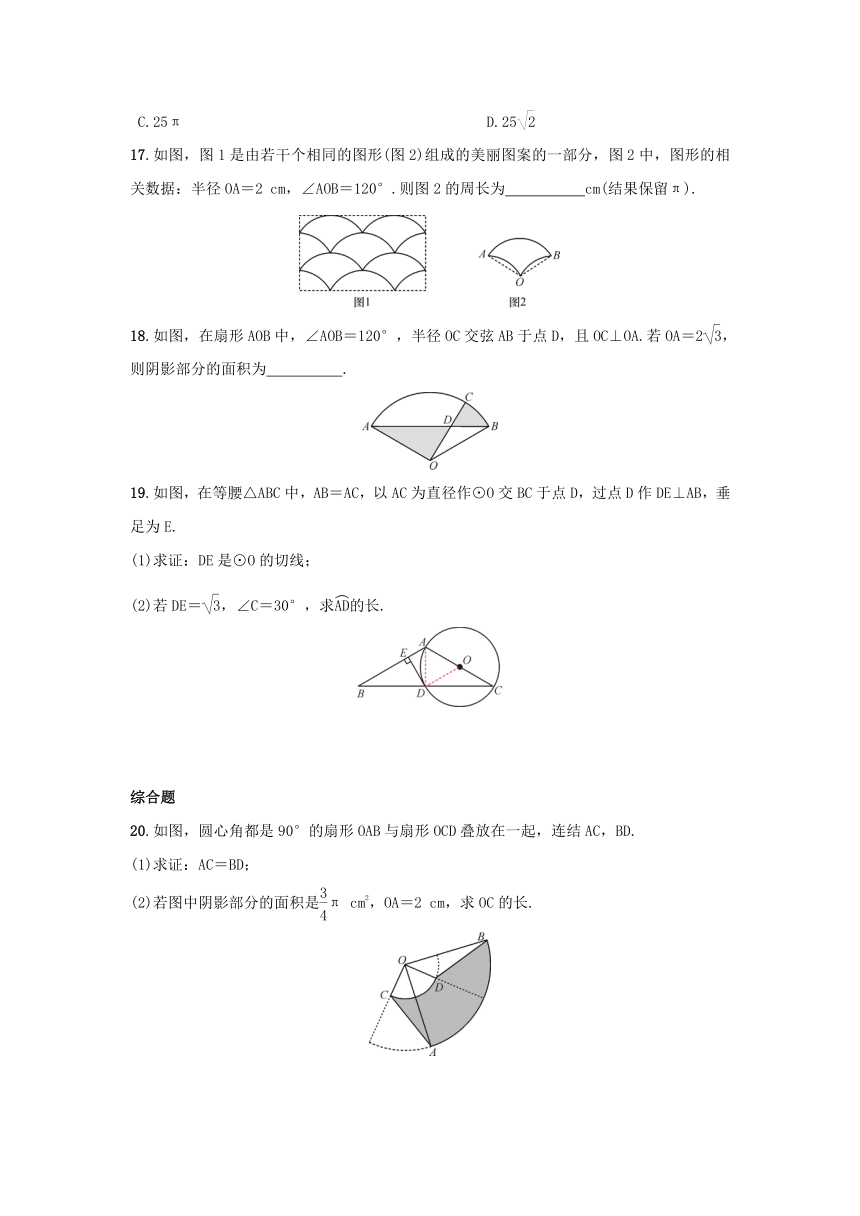
A.π B.2π
C.3π D.6π
2.一个扇形的半径为8 cm,弧长为π cm,则扇形的圆心角为( )
A.60° B.120°
C.150° D.180°
3.一个扇形的圆心角为120°,弧长为π cm,则该扇形的半径为( )
A.4 cm B.5 cm
C.8 cm D.10 cm
4.如图,用一个半径为5 cm的定滑轮带动重物上升,滑轮上一点P旋转了108°,假设绳索(粗细不计)与滑轮之间没有滑动,则重物上升了( )
A.π cm B.2π cm
C.3π cm D.5π cm
5.如图,PA,PB是⊙O的切线,切点分别为A,B.若OA=2,∠P=60°,则的长为( )
A.π B.π C.π D.π
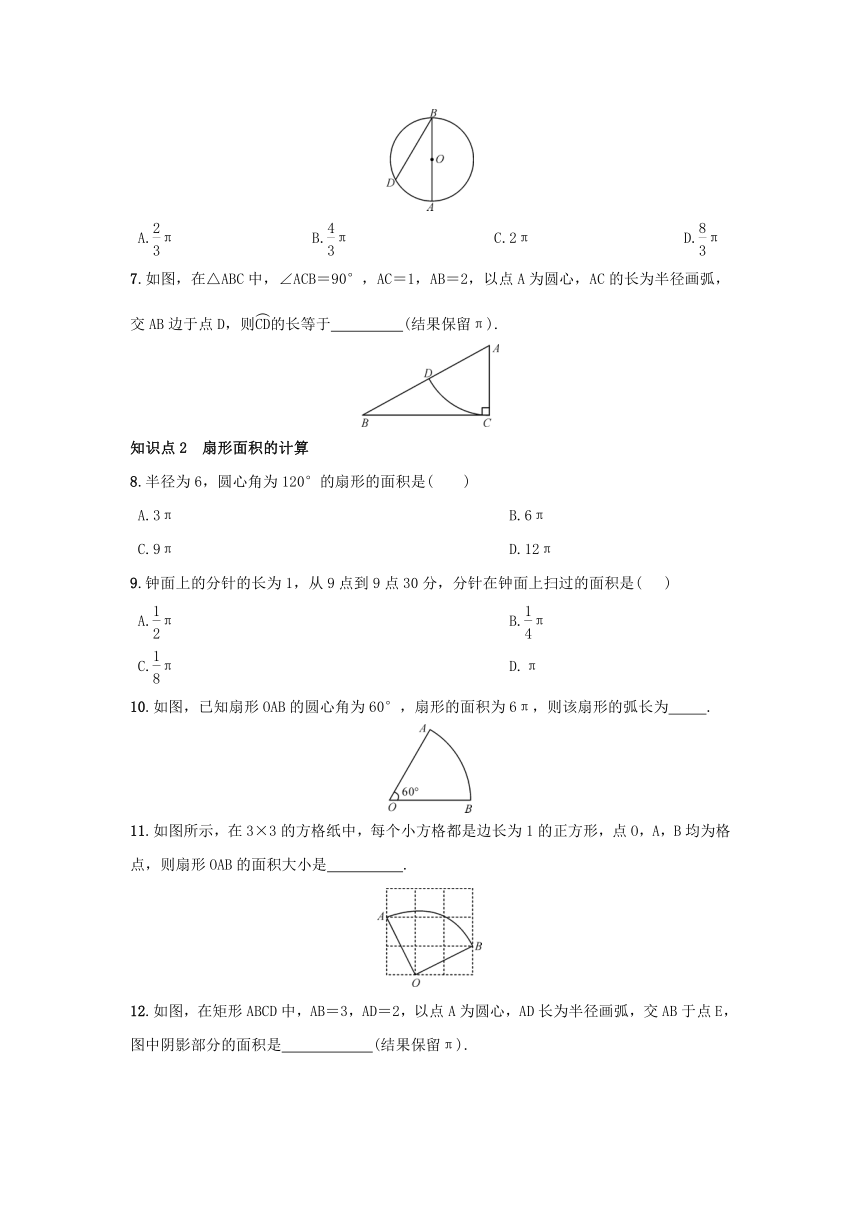
6.(2018·黄石)如图,AB是⊙O的直径,点D为⊙O上一点,且∠ABD=30°,BO=4,则的长为( )
A.π B.π C.2π D.π
7.如图,在△ABC中,∠ACB=90°,AC=1,AB=2,以点A为圆心,AC的长为半径画弧,交AB边于点D,则的长等于 (结果保留π).
知识点2 扇形面积的计算
8.半径为6,圆心角为120°的扇形的面积是( )
A.3π B.6π
C.9π D.12π
9.钟面上的分针的长为1,从9点到9点30分,分针在钟面上扫过的面积是( )
A.π B.π
C.π D.π
10.如图,已知扇形OAB的圆心角为60°,扇形的面积为6π,则该扇形的弧长为 .
11.如图所示,在3×3的方格纸中,每个小方格都是边长为1的正方形,点O,A,B均为格点,则扇形OAB的面积大小是 .
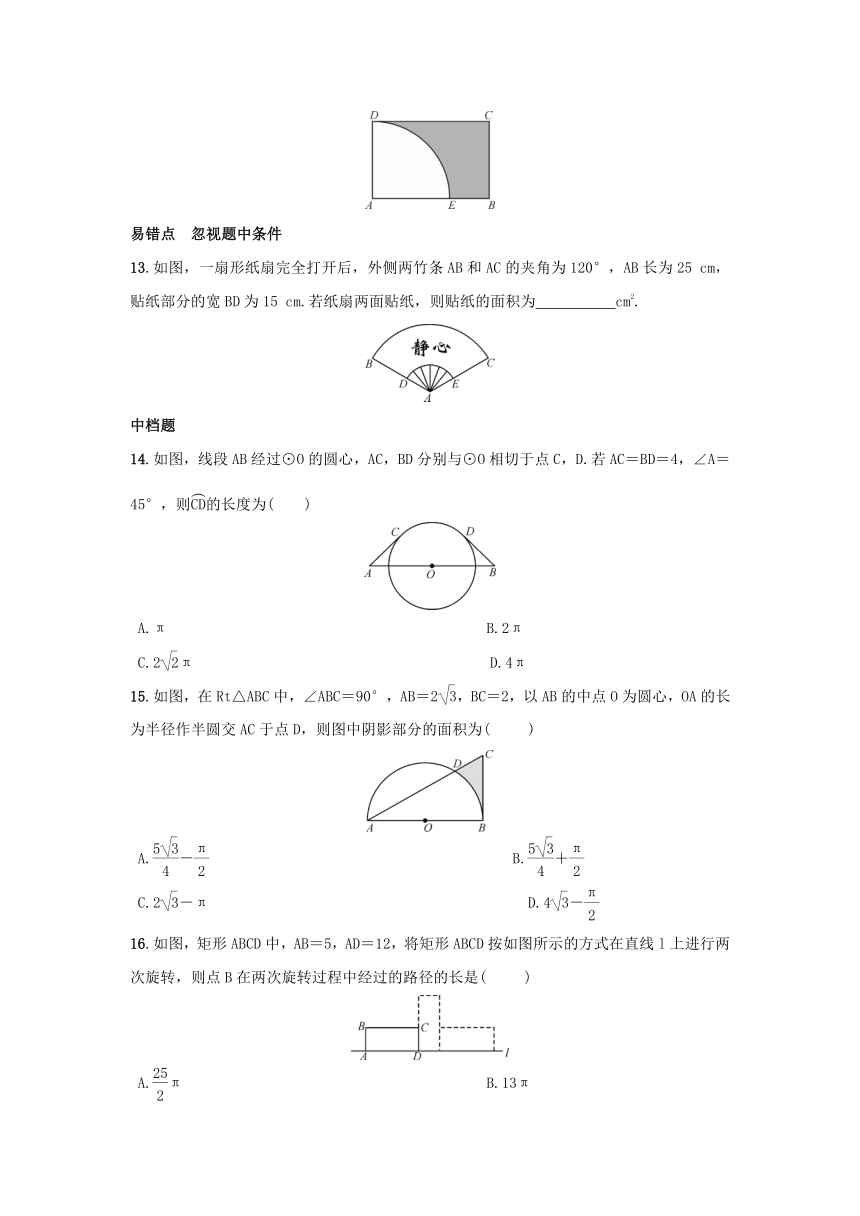
12.如图,在矩形ABCD中,AB=3,AD=2,以点A为圆心,AD长为半径画弧,交AB于点E,图中阴影部分的面积是 (结果保留π).
易错点 忽视题中条件
13.如图,一扇形纸扇完全打开后,外侧两竹条AB和AC的夹角为120°,AB长为25 cm,贴纸部分的宽BD为15 cm.若纸扇两面贴纸,则贴纸的面积为 cm2.
中档题
14.如图,线段AB经过⊙O的圆心,AC,BD分别与⊙O相切于点C,D.若AC=BD=4,∠A=45°,则的长度为( )
A.π B.2π
C.2π D.4π
15.如图,在Rt△ABC中,∠ABC=90°,AB=2,BC=2,以AB的中点O为圆心,OA的长为半径作半圆交AC于点D,则图中阴影部分的面积为( )
A.- B.+
C.2-π D.4-
16.如图,矩形ABCD中,AB=5,AD=12,将矩形ABCD按如图所示的方式在直线l上进行两次旋转,则点B在两次旋转过程中经过的路径的长是( )
A.π B.13π
C.25π D.25
17.如图,图1是由若干个相同的图形(图2)组成的美丽图案的一部分,图2中,图形的相关数据:半径OA=2 cm,∠AOB=120°.则图2的周长为 cm(结果保留π).
18.如图,在扇形AOB中,∠AOB=120°,半径OC交弦AB于点D,且OC⊥OA.若OA=2,则阴影部分的面积为 .
19.如图,在等腰△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作DE⊥AB,垂足为E.
(1)求证:DE是⊙O的切线;
(2)若DE=,∠C=30°,求的长.
综合题
20.如图,圆心角都是90°的扇形OAB与扇形OCD叠放在一起,连结AC,BD.
(1)求证:AC=BD;
(2)若图中阴影部分的面积是π cm2,OA=2 cm,求OC的长.
2020春华师大版九下数学27.3第1课时弧长与扇形的面积同步课堂练习(教师版)
基础题
知识点1 弧长的计算
1.若扇形的圆心角为90°,半径为6,则该扇形的弧长为(C)
A.π B.2π
C.3π D.6π
2.一个扇形的半径为8 cm,弧长为π cm,则扇形的圆心角为(B)
A.60° B.120°
C.150° D.180°
3.一个扇形的圆心角为120°,弧长为π cm,则该扇形的半径为(C)
A.4 cm B.5 cm
C.8 cm D.10 cm
4.如图,用一个半径为5 cm的定滑轮带动重物上升,滑轮上一点P旋转了108°,假设绳索(粗细不计)与滑轮之间没有滑动,则重物上升了(C)
A.π cm B.2π cm
C.3π cm D.5π cm
5.如图,PA,PB是⊙O的切线,切点分别为A,B.若OA=2,∠P=60°,则的长为(C)
A.π B.π C.π D.π
6.(2018·黄石)如图,AB是⊙O的直径,点D为⊙O上一点,且∠ABD=30°,BO=4,则的长为(D)
A.π B.π C.2π D.π
7.如图,在△ABC中,∠ACB=90°,AC=1,AB=2,以点A为圆心,AC的长为半径画弧,交AB边于点D,则的长等于(结果保留π).
知识点2 扇形面积的计算
8.半径为6,圆心角为120°的扇形的面积是(D)
A.3π B.6π
C.9π D.12π
9.钟面上的分针的长为1,从9点到9点30分,分针在钟面上扫过的面积是(A)
A.π B.π
C.π D.π
10.如图,已知扇形OAB的圆心角为60°,扇形的面积为6π,则该扇形的弧长为2π.
11.如图所示,在3×3的方格纸中,每个小方格都是边长为1的正方形,点O,A,B均为格点,则扇形OAB的面积大小是π.
12.如图,在矩形ABCD中,AB=3,AD=2,以点A为圆心,AD长为半径画弧,交AB于点E,图中阴影部分的面积是6-π(结果保留π).
易错点 忽视题中条件
13.如图,一扇形纸扇完全打开后,外侧两竹条AB和AC的夹角为120°,AB长为25 cm,贴纸部分的宽BD为15 cm.若纸扇两面贴纸,则贴纸的面积为350πcm2.
中档题
14.如图,线段AB经过⊙O的圆心,AC,BD分别与⊙O相切于点C,D.若AC=BD=4,∠A=45°,则的长度为(B)
A.π B.2π
C.2π D.4π
15.如图,在Rt△ABC中,∠ABC=90°,AB=2,BC=2,以AB的中点O为圆心,OA的长为半径作半圆交AC于点D,则图中阴影部分的面积为(A)
A.- B.+
C.2-π D.4-
16.如图,矩形ABCD中,AB=5,AD=12,将矩形ABCD按如图所示的方式在直线l上进行两次旋转,则点B在两次旋转过程中经过的路径的长是(A)
A.π B.13π
C.25π D.25
17.如图,图1是由若干个相同的图形(图2)组成的美丽图案的一部分,图2中,图形的相关数据:半径OA=2 cm,∠AOB=120°.则图2的周长为cm(结果保留π).
18.如图,在扇形AOB中,∠AOB=120°,半径OC交弦AB于点D,且OC⊥OA.若OA=2,则阴影部分的面积为+π.
19.如图,在等腰△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作DE⊥AB,垂足为E.
(1)求证:DE是⊙O的切线;
(2)若DE=,∠C=30°,求的长.
解:(1)证明:连结OD.
∵OC=OD,AB=AC,
∴∠ODC=∠C,∠C=∠B.
∴∠ODC=∠B.
∴OD∥AB.
∵DE⊥AB,
∴DE⊥OD.
又∵OD是⊙O的半径,
∴DE为⊙O的切线.
(2)连结AD.∵AC为⊙O的直径,
∴∠ADC=90°,即AD⊥BC.
∵AB=AC,
∴∠B=∠C=30°,BD=CD.
∵DE=,
∴BD=CD=2.
∴OA=AC=×=2.
∵∠AOD=∠ODC+∠C=2∠C=60°,
∴的长为=π.
综合题
20.如图,圆心角都是90°的扇形OAB与扇形OCD叠放在一起,连结AC,BD.
(1)求证:AC=BD;
(2)若图中阴影部分的面积是π cm2,OA=2 cm,求OC的长.
解:(1)证明:∵∠AOB=∠COD=90°,
∴∠AOC+∠AOD=∠BOD+∠AOD.
∴∠AOC=∠BOD.
又∵AO=BO,CO=DO,
∴△AOC≌△BOD(SAS).∴AC=BD.
(2)根据题意,得
S阴影=-
=,
∴π=,解得OC=1(负值舍去).
∴OC=1 cm.
基础题
知识点1 弧长的计算
1.若扇形的圆心角为90°,半径为6,则该扇形的弧长为( )
A.π B.2π
C.3π D.6π
2.一个扇形的半径为8 cm,弧长为π cm,则扇形的圆心角为( )
A.60° B.120°
C.150° D.180°
3.一个扇形的圆心角为120°,弧长为π cm,则该扇形的半径为( )
A.4 cm B.5 cm
C.8 cm D.10 cm
4.如图,用一个半径为5 cm的定滑轮带动重物上升,滑轮上一点P旋转了108°,假设绳索(粗细不计)与滑轮之间没有滑动,则重物上升了( )
A.π cm B.2π cm
C.3π cm D.5π cm
5.如图,PA,PB是⊙O的切线,切点分别为A,B.若OA=2,∠P=60°,则的长为( )
A.π B.π C.π D.π
6.(2018·黄石)如图,AB是⊙O的直径,点D为⊙O上一点,且∠ABD=30°,BO=4,则的长为( )
A.π B.π C.2π D.π
7.如图,在△ABC中,∠ACB=90°,AC=1,AB=2,以点A为圆心,AC的长为半径画弧,交AB边于点D,则的长等于 (结果保留π).
知识点2 扇形面积的计算
8.半径为6,圆心角为120°的扇形的面积是( )
A.3π B.6π
C.9π D.12π
9.钟面上的分针的长为1,从9点到9点30分,分针在钟面上扫过的面积是( )
A.π B.π
C.π D.π
10.如图,已知扇形OAB的圆心角为60°,扇形的面积为6π,则该扇形的弧长为 .
11.如图所示,在3×3的方格纸中,每个小方格都是边长为1的正方形,点O,A,B均为格点,则扇形OAB的面积大小是 .
12.如图,在矩形ABCD中,AB=3,AD=2,以点A为圆心,AD长为半径画弧,交AB于点E,图中阴影部分的面积是 (结果保留π).
易错点 忽视题中条件
13.如图,一扇形纸扇完全打开后,外侧两竹条AB和AC的夹角为120°,AB长为25 cm,贴纸部分的宽BD为15 cm.若纸扇两面贴纸,则贴纸的面积为 cm2.
中档题
14.如图,线段AB经过⊙O的圆心,AC,BD分别与⊙O相切于点C,D.若AC=BD=4,∠A=45°,则的长度为( )
A.π B.2π
C.2π D.4π
15.如图,在Rt△ABC中,∠ABC=90°,AB=2,BC=2,以AB的中点O为圆心,OA的长为半径作半圆交AC于点D,则图中阴影部分的面积为( )
A.- B.+
C.2-π D.4-
16.如图,矩形ABCD中,AB=5,AD=12,将矩形ABCD按如图所示的方式在直线l上进行两次旋转,则点B在两次旋转过程中经过的路径的长是( )
A.π B.13π
C.25π D.25
17.如图,图1是由若干个相同的图形(图2)组成的美丽图案的一部分,图2中,图形的相关数据:半径OA=2 cm,∠AOB=120°.则图2的周长为 cm(结果保留π).
18.如图,在扇形AOB中,∠AOB=120°,半径OC交弦AB于点D,且OC⊥OA.若OA=2,则阴影部分的面积为 .
19.如图,在等腰△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作DE⊥AB,垂足为E.
(1)求证:DE是⊙O的切线;
(2)若DE=,∠C=30°,求的长.
综合题
20.如图,圆心角都是90°的扇形OAB与扇形OCD叠放在一起,连结AC,BD.
(1)求证:AC=BD;
(2)若图中阴影部分的面积是π cm2,OA=2 cm,求OC的长.
2020春华师大版九下数学27.3第1课时弧长与扇形的面积同步课堂练习(教师版)
基础题
知识点1 弧长的计算
1.若扇形的圆心角为90°,半径为6,则该扇形的弧长为(C)
A.π B.2π
C.3π D.6π
2.一个扇形的半径为8 cm,弧长为π cm,则扇形的圆心角为(B)
A.60° B.120°
C.150° D.180°
3.一个扇形的圆心角为120°,弧长为π cm,则该扇形的半径为(C)
A.4 cm B.5 cm
C.8 cm D.10 cm
4.如图,用一个半径为5 cm的定滑轮带动重物上升,滑轮上一点P旋转了108°,假设绳索(粗细不计)与滑轮之间没有滑动,则重物上升了(C)
A.π cm B.2π cm
C.3π cm D.5π cm
5.如图,PA,PB是⊙O的切线,切点分别为A,B.若OA=2,∠P=60°,则的长为(C)
A.π B.π C.π D.π
6.(2018·黄石)如图,AB是⊙O的直径,点D为⊙O上一点,且∠ABD=30°,BO=4,则的长为(D)
A.π B.π C.2π D.π
7.如图,在△ABC中,∠ACB=90°,AC=1,AB=2,以点A为圆心,AC的长为半径画弧,交AB边于点D,则的长等于(结果保留π).
知识点2 扇形面积的计算
8.半径为6,圆心角为120°的扇形的面积是(D)
A.3π B.6π
C.9π D.12π
9.钟面上的分针的长为1,从9点到9点30分,分针在钟面上扫过的面积是(A)
A.π B.π
C.π D.π
10.如图,已知扇形OAB的圆心角为60°,扇形的面积为6π,则该扇形的弧长为2π.
11.如图所示,在3×3的方格纸中,每个小方格都是边长为1的正方形,点O,A,B均为格点,则扇形OAB的面积大小是π.
12.如图,在矩形ABCD中,AB=3,AD=2,以点A为圆心,AD长为半径画弧,交AB于点E,图中阴影部分的面积是6-π(结果保留π).
易错点 忽视题中条件
13.如图,一扇形纸扇完全打开后,外侧两竹条AB和AC的夹角为120°,AB长为25 cm,贴纸部分的宽BD为15 cm.若纸扇两面贴纸,则贴纸的面积为350πcm2.
中档题
14.如图,线段AB经过⊙O的圆心,AC,BD分别与⊙O相切于点C,D.若AC=BD=4,∠A=45°,则的长度为(B)
A.π B.2π
C.2π D.4π
15.如图,在Rt△ABC中,∠ABC=90°,AB=2,BC=2,以AB的中点O为圆心,OA的长为半径作半圆交AC于点D,则图中阴影部分的面积为(A)
A.- B.+
C.2-π D.4-
16.如图,矩形ABCD中,AB=5,AD=12,将矩形ABCD按如图所示的方式在直线l上进行两次旋转,则点B在两次旋转过程中经过的路径的长是(A)
A.π B.13π
C.25π D.25
17.如图,图1是由若干个相同的图形(图2)组成的美丽图案的一部分,图2中,图形的相关数据:半径OA=2 cm,∠AOB=120°.则图2的周长为cm(结果保留π).
18.如图,在扇形AOB中,∠AOB=120°,半径OC交弦AB于点D,且OC⊥OA.若OA=2,则阴影部分的面积为+π.
19.如图,在等腰△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作DE⊥AB,垂足为E.
(1)求证:DE是⊙O的切线;
(2)若DE=,∠C=30°,求的长.
解:(1)证明:连结OD.
∵OC=OD,AB=AC,
∴∠ODC=∠C,∠C=∠B.
∴∠ODC=∠B.
∴OD∥AB.
∵DE⊥AB,
∴DE⊥OD.
又∵OD是⊙O的半径,
∴DE为⊙O的切线.
(2)连结AD.∵AC为⊙O的直径,
∴∠ADC=90°,即AD⊥BC.
∵AB=AC,
∴∠B=∠C=30°,BD=CD.
∵DE=,
∴BD=CD=2.
∴OA=AC=×=2.
∵∠AOD=∠ODC+∠C=2∠C=60°,
∴的长为=π.
综合题
20.如图,圆心角都是90°的扇形OAB与扇形OCD叠放在一起,连结AC,BD.
(1)求证:AC=BD;
(2)若图中阴影部分的面积是π cm2,OA=2 cm,求OC的长.
解:(1)证明:∵∠AOB=∠COD=90°,
∴∠AOC+∠AOD=∠BOD+∠AOD.
∴∠AOC=∠BOD.
又∵AO=BO,CO=DO,
∴△AOC≌△BOD(SAS).∴AC=BD.
(2)根据题意,得
S阴影=-
=,
∴π=,解得OC=1(负值舍去).
∴OC=1 cm.
