2020年春沪教版(上海)七年级数学下册第十五章《平面直角坐标系》同步复习课件(34张)
文档属性
| 名称 | 2020年春沪教版(上海)七年级数学下册第十五章《平面直角坐标系》同步复习课件(34张) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-20 21:26:22 | ||
图片预览









文档简介
(共33张PPT)
第17讲 平面直角坐标系
1.答案:△PDQ是等腰直角三角形
证明:∵ABCD是正方形,
∴AD=CD,∠A=∠ADC=∠BCD=∠DCQ=90°,
又∵CQ=AP,
∴△ADP≌ △CDQ( SAS ),
∴ DP = DQ,∠ADP = ∠CDQ
∴∠A DP +∠CDP = ∠C DQ +∠C DP = 90°
∴△PDQ是等腰直角三角形
2.答案:通过证明 ABD≌ ACE,,得到∠ACE=∠B=60°=∠BAC,从而得证。
证明:∵△ABC和△ADE是等边三角形,
∴∠BAC=∠DAE=60°,
又∵∠BAC=∠BAD+∠DAC,∠DAE=∠EAC+∠DAC,
∴∠BAD=∠EAC,
∴ ABD≌ ACE(SAS),
∴∠ACE=∠B=60°=∠BAC,
∴AB//CE.
上次课后答案
3.证明:过点E作EH⊥BC,垂足为H,
∴∠EHC=90°,
又由已知条件∠BAC=90°,EC为∠BAC的角平分线,
∴∠ACE=∠BCE,
∴△ACE≌△HCE(AAS),
∴AE=EH,∠HEC=∠AEC,
又∵AD⊥BC,∴EH//AD,
∴∠HEC=∠AFE,
∴∠AEF=∠AFE,∴AE=AF,
∴AF=EH,
△AGF≌△EBH(AAS),
∴AG=BE,
又∵AG=GE+AE,BE=GE+BG,
∴BG=AE.
4.证明:∵BD=BE,∠BAD=∠BCE,∠B=∠B,
∴△ABD≌△BCE(AAS),
∴AB=BC,∠BAD=∠BCE,
∴∠BAC=∠BCA,
又∵∠BAC=∠BAD+∠DAC,
∠BCA=∠BCE+∠ECA,
∴∠DAC=∠ECA,
∴AF=FC,
∴△AFC为等腰三角形.
6.证明: ∵AC CD于C
BD CD于D
∴AC∥BD(同垂直于一条直
线的两条直线平行)
有 A = B(两直线平行内错
角相等)
∵M是AB中点
∴AM = BM
又∵ AMC = BMF(对顶角相
等)
∴△ACM=△BFM(SAS)
7.证明: 在AB上截取AE = AD, 连接EC,
∵AC平分 DAE,
∴ DAC = EAC,
故△ACD≌△ACE (SAS),
CD = CE (全等三解形对应边相等),
D = AEC ,
又∵ D + B = 180 (已知),
∴ AEC + B = 180 (等量代换),
又∵ AEC + CEB = 180 (平角定义),
∴ B = CEB (同角的补角相等),
CE = CB (在一个三角形中等角对等边),
∴CD = CB (等量代换).
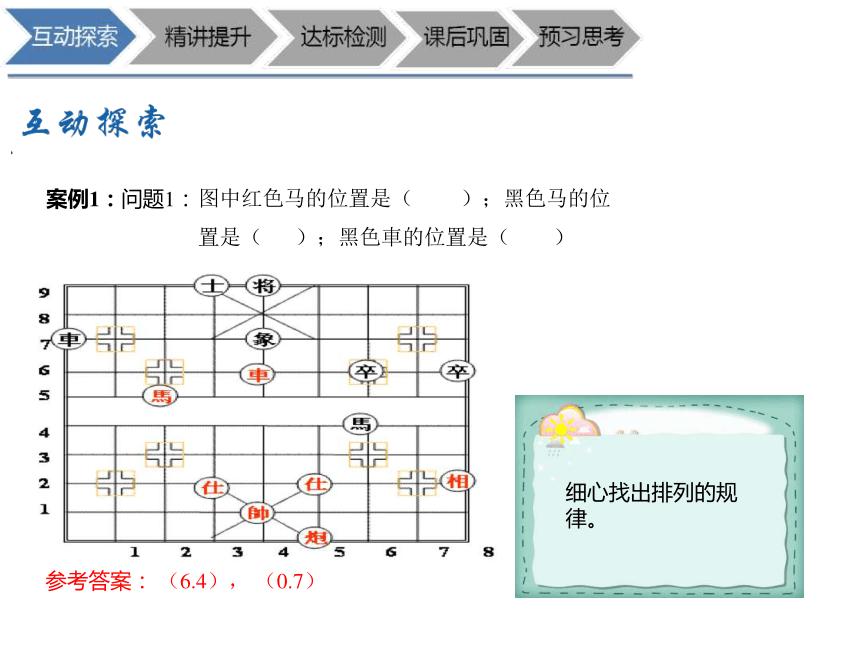
案例1:问题1:
参考答案: (6.4), (0.7)
细心找出排列的规律。
图中红色马的位置是( );黑色马的位置是( );黑色車的位置是( )
知识点一:平面直角坐标系内的点
1.在平面内,两条互相垂直且有公共原点的数轴组成平面直角坐标系,通常两条数轴分别置于水平位置与铅直位置,水平的数轴向右为正叫做 X 轴(横轴),铅直的数轴向上为正叫做 Y 轴(纵轴);X 轴和Y 轴统称为坐标轴,它们的公共原点 O称为直角坐标系的原点,建立了直角坐标系的平面叫做坐标平面 。坐标平面由两条坐标轴和四个象限构成,可以看成坐标平面的六个区域
X 轴,Y 轴,第一象限,第二象限,第三象限,第四象限
2.注意:坐标轴上的点不属于任何一个象限。
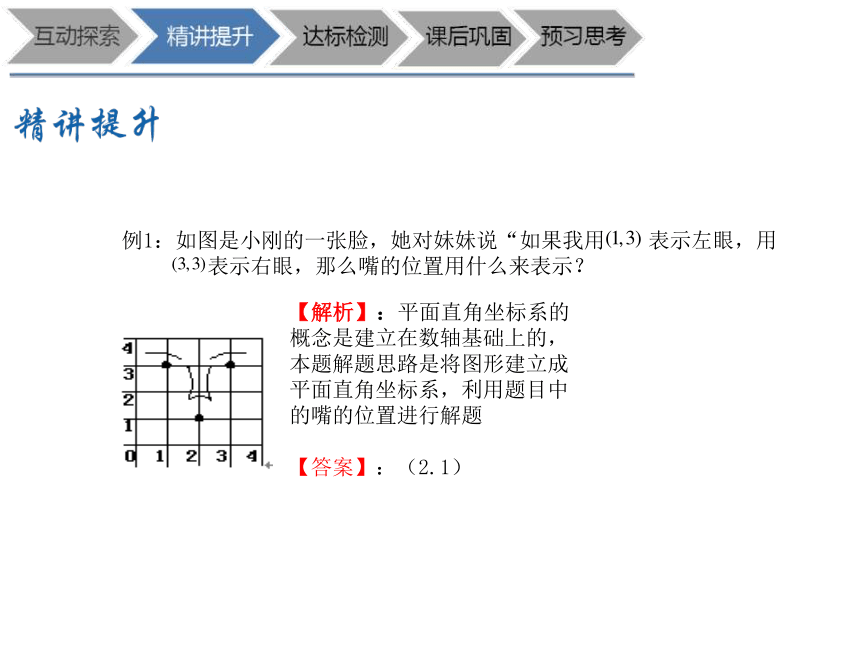
例1:如图是小刚的一张脸,她对妹妹说“如果我用 表示左眼,用
表示右眼,那么嘴的位置用什么来表示?
【解析】:平面直角坐标系的概念是建立在数轴基础上的,本题解题思路是将图形建立成平面直角坐标系,利用题目中的嘴的位置进行解题
【答案】:(2.1)
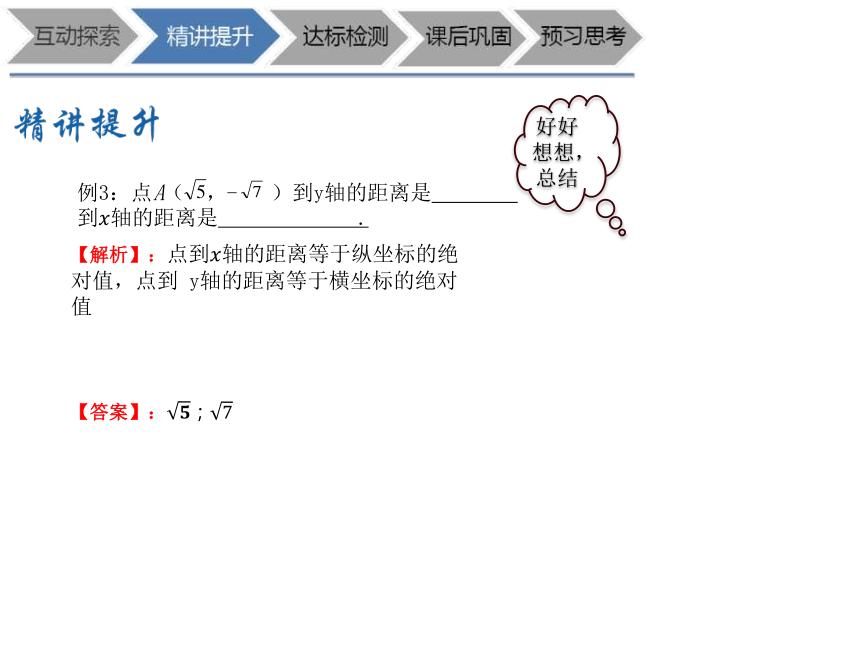
例3:点 ( , )到y轴的距离是
到轴的距离是 .
【解析】:点到轴的距离等于纵坐标的绝对值,点到 y轴的距离等于横坐标的绝对值
【答案】:;
好好想想,总结
试一试:(1)点 A在第二象限 ,它到轴、y轴距离分别是 、 ,则
坐标是
【解析】:点是,
【答案】:(-,-2);(-,2);( ,2);(,-2)
(2)平面上有点P ,P点到坐标轴的距离均为正整数,若点P 到X轴、Y
轴的距离之积等于10,试写出符合条件的点的坐标。
【解析】:点到X轴的距离为纵坐标的绝对值,到Y轴的距离横坐标的绝对值。
【答案】:(2.5);(5.2) (答案不唯一)
坐标点到坐标轴的距离都为正数
,
知识点二:象限内点的特征
第一象限:(+,+),则x>0,y>0; 第二象限:(-,+),则x<0,y>0;
第三象限:(-,-),则x<0,y<0; 第四象限:(+,-),则x>0,y<0
在x轴上:(x,0),则y=0; 在y轴上:(0,y),则x=0;
坐标原点:(0,0),则x=0,y=0;
知识总结
例1、已知点 P( , ),在第三象限,则 的取值范围是( )
A、 B、 C、 D、
【解析】:第三象限的点的特征是横纵坐标都位负数,根据题意可用不等式进行解答
【答案】: ,A
第三象限:(-,-),则x<0,y<0;
例2:已知点 的坐标为(。
【解析】:根据横纵坐标的积等于正数可知两坐标同号,根据和为负数,可以知道两个坐标值都为负数。
【答案】:三
巩固练习:
1、若点 、三象限两坐标轴的角平分线上,则是( )
【解析】:根据点在一、三象限角平分线上的特点,可以知道点的横纵坐标值相等
【答案】:
知识点归纳
在象限的角平分线上的点的横纵坐标相等或者互为相反数
知识点三:平面直角坐标系内点的对称性、平移、旋转
例1、如图,线段 逆时针旋转90后,点至点,则点的坐标是( )
如果将绕原点顺时针旋转90后,点至点,则的坐标是( )
【解析】:过点
【答案】:B(-3,-1),C(3,1)
例2:在直角坐标平面内,已知正方形的顶点的坐标是,顶点是,则点的坐标是什么?
观察形式 ,想想以前学过的知识
【解析】:过分别向坐
标轴作垂线构造全等三角形
【答案】: C(5,2),D(3,5)
1.已知点A(3,-1)与点B关于原点对称,则点B的坐标为_______________。
2.经过点 (2,7)且垂直于 直线可表示为
3. 到距离为3的点所在的直线是 。
4. 已知点A(0,a),点B(1,0),直线AB与坐标轴围成的三角形面积为4,则a=_______________。
5. 点A(1+m,m)向上平移2个单位至点A’,若点A与A’恰好关于x轴对称,则点A’坐标是_____________。
6. 将点P(-3,y)向下平移3个单位,向左平移2个单位后得到点Q(x,-1),则xy=_______________。
(-3,1)
y=7
x=3或x=-3
8或-8
(0,1)
-10
7. 点P (2,3) 绕着原点O逆时针旋转90°后得到的点Q的坐标是 _______________。
8. 已知长方形ABCD中,AB=5,BC=8,并且AB∥x轴,若点A的坐标为(-2,4),则点C的坐标为_______________。
9. 已知平面直角坐标系中点P的纵坐标是2,且点P到y轴的距离是3,则点P的坐标为___________ ____。
直角坐标平面内,点直 两坐标轴围成的三角形的面积是6,则点的坐标是 _______________
(-3,2)
(3,12)
(3,2)或(-3,2)
(0,3)或(0,-3)
11.已知点A(-1,0)和点B(1,2),要在一个点,使得为等腰三角形,则满足这样条件的点P共有( )
A.2个 B.3个 C.4个 D.5个
12. 点 P (– 5,1 – t ) 与点Q (k,4) 关于原点对称,则 3k – 2 t 的值为 ( )
A、– 25 B、25 C、5 D、– 5
13. 点M (2 – a,a + 1)在第二象限,则a的取值范围是 ( )
A、a < 2 B、– 1 < a < 2 C、a > – 1 D、a > 2
14. 已知点 P (m + 1,– 1) 在第二、四象限的角平分线上,则 m的值为 ( )
A、1 B、0 C、– 1 D、– 2
C
C
D
B
15. 如图,写出各顶点的坐标,判断的形状,并求的面积?
答案:A(-8,3),B(-3,0),C(0,5),等腰直角三角形
16. 已知点,点为坐标原点,点为点,
线段旋转90。
(1)试在坐标平面内画、点的位置,并写出它们的坐标
(2)求的面积
答案:(1)B(-2,4),C(4,-2);(2)6
17. 已知亮点的坐标,如图所示,
(1)求的面积
(2)若点满足条件的点的坐标
答案:(1)8,
(2)(0,2)、(0,-2)
18. 如图,平行四边形ABCD的顶点A、B、C的坐标分别为 A(– 2,4)、 B (– 2,0)、C (4,– 1),求点D的坐标及平行四边形ABCD的面积
答案:D的坐标为(4,3),平行四边形ABCD的面积为24
19. 如图为风筝的图案.
(1)若原点用字母表示,写出图中点A,B,C的坐标
(2)试求(1)中风筝所覆盖的平面的面积.
答案:(1) A(0,7), B(-3,1),
C(-3,-1)
(2) 27
对比学习
20. 在平面直角坐标系中,一蚂蚁从原点 出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位.其行走路线如下图所示.
(1)填写下列各点的坐标:A4( , ),A8( , ),A12( , );
(2)写出点A4n的坐标(n是正整数);
(3)指出蚂蚁从点A100到点A101的移动方向.
认真思考,你最棒
1.直角坐标平面内,点 A 到x 轴的距离为2,到为3,则点A为( )
2.直角坐标平面内点 ,关于轴的对称的点在第四象限 ,则的
取值范围是 _______________
3.已知点向左平移4个单位到达点,点关于原点的对称点为
则点的坐标是_______________。
4.在平面直角坐标系中,点找一点,使得为顶点构成的三角形是等腰三角形,则这样的点有_______________个.
6.已知点A(-1,2)、B(-3,-2)、C(-1,-3)、D(0,1),画出四边形ABCD,并求其面积。
7.已知点A(2,3)与点B(2,0),在直角坐标平面内描出两点,画出以A、B为顶点的正方形,并写出另外两顶点的坐标。
8.如图,矩形的顶点 为坐标原点,点A 在轴上,点B的坐标为(2,1)
如果将矩形绕点旋转180°,旋转后的图形为矩形 OA1B1C1那么点B1 的坐标为_______________。.
9.如图,A,B的坐标为(2,0),(0,1)若将线段A B平移至 ,则的值为_______________。
10.在平面直角坐标系中,O是坐标原点,已知A点的坐标为(1,1),请你在坐标轴上找出点B,使△AOB为等腰三角形,则符合条件的点B共有_______________。
第17讲 平面直角坐标系
1.答案:△PDQ是等腰直角三角形
证明:∵ABCD是正方形,
∴AD=CD,∠A=∠ADC=∠BCD=∠DCQ=90°,
又∵CQ=AP,
∴△ADP≌ △CDQ( SAS ),
∴ DP = DQ,∠ADP = ∠CDQ
∴∠A DP +∠CDP = ∠C DQ +∠C DP = 90°
∴△PDQ是等腰直角三角形
2.答案:通过证明 ABD≌ ACE,,得到∠ACE=∠B=60°=∠BAC,从而得证。
证明:∵△ABC和△ADE是等边三角形,
∴∠BAC=∠DAE=60°,
又∵∠BAC=∠BAD+∠DAC,∠DAE=∠EAC+∠DAC,
∴∠BAD=∠EAC,
∴ ABD≌ ACE(SAS),
∴∠ACE=∠B=60°=∠BAC,
∴AB//CE.
上次课后答案
3.证明:过点E作EH⊥BC,垂足为H,
∴∠EHC=90°,
又由已知条件∠BAC=90°,EC为∠BAC的角平分线,
∴∠ACE=∠BCE,
∴△ACE≌△HCE(AAS),
∴AE=EH,∠HEC=∠AEC,
又∵AD⊥BC,∴EH//AD,
∴∠HEC=∠AFE,
∴∠AEF=∠AFE,∴AE=AF,
∴AF=EH,
△AGF≌△EBH(AAS),
∴AG=BE,
又∵AG=GE+AE,BE=GE+BG,
∴BG=AE.
4.证明:∵BD=BE,∠BAD=∠BCE,∠B=∠B,
∴△ABD≌△BCE(AAS),
∴AB=BC,∠BAD=∠BCE,
∴∠BAC=∠BCA,
又∵∠BAC=∠BAD+∠DAC,
∠BCA=∠BCE+∠ECA,
∴∠DAC=∠ECA,
∴AF=FC,
∴△AFC为等腰三角形.
6.证明: ∵AC CD于C
BD CD于D
∴AC∥BD(同垂直于一条直
线的两条直线平行)
有 A = B(两直线平行内错
角相等)
∵M是AB中点
∴AM = BM
又∵ AMC = BMF(对顶角相
等)
∴△ACM=△BFM(SAS)
7.证明: 在AB上截取AE = AD, 连接EC,
∵AC平分 DAE,
∴ DAC = EAC,
故△ACD≌△ACE (SAS),
CD = CE (全等三解形对应边相等),
D = AEC ,
又∵ D + B = 180 (已知),
∴ AEC + B = 180 (等量代换),
又∵ AEC + CEB = 180 (平角定义),
∴ B = CEB (同角的补角相等),
CE = CB (在一个三角形中等角对等边),
∴CD = CB (等量代换).
案例1:问题1:
参考答案: (6.4), (0.7)
细心找出排列的规律。
图中红色马的位置是( );黑色马的位置是( );黑色車的位置是( )
知识点一:平面直角坐标系内的点
1.在平面内,两条互相垂直且有公共原点的数轴组成平面直角坐标系,通常两条数轴分别置于水平位置与铅直位置,水平的数轴向右为正叫做 X 轴(横轴),铅直的数轴向上为正叫做 Y 轴(纵轴);X 轴和Y 轴统称为坐标轴,它们的公共原点 O称为直角坐标系的原点,建立了直角坐标系的平面叫做坐标平面 。坐标平面由两条坐标轴和四个象限构成,可以看成坐标平面的六个区域
X 轴,Y 轴,第一象限,第二象限,第三象限,第四象限
2.注意:坐标轴上的点不属于任何一个象限。
例1:如图是小刚的一张脸,她对妹妹说“如果我用 表示左眼,用
表示右眼,那么嘴的位置用什么来表示?
【解析】:平面直角坐标系的概念是建立在数轴基础上的,本题解题思路是将图形建立成平面直角坐标系,利用题目中的嘴的位置进行解题
【答案】:(2.1)
例3:点 ( , )到y轴的距离是
到轴的距离是 .
【解析】:点到轴的距离等于纵坐标的绝对值,点到 y轴的距离等于横坐标的绝对值
【答案】:;
好好想想,总结
试一试:(1)点 A在第二象限 ,它到轴、y轴距离分别是 、 ,则
坐标是
【解析】:点是,
【答案】:(-,-2);(-,2);( ,2);(,-2)
(2)平面上有点P ,P点到坐标轴的距离均为正整数,若点P 到X轴、Y
轴的距离之积等于10,试写出符合条件的点的坐标。
【解析】:点到X轴的距离为纵坐标的绝对值,到Y轴的距离横坐标的绝对值。
【答案】:(2.5);(5.2) (答案不唯一)
坐标点到坐标轴的距离都为正数
,
知识点二:象限内点的特征
第一象限:(+,+),则x>0,y>0; 第二象限:(-,+),则x<0,y>0;
第三象限:(-,-),则x<0,y<0; 第四象限:(+,-),则x>0,y<0
在x轴上:(x,0),则y=0; 在y轴上:(0,y),则x=0;
坐标原点:(0,0),则x=0,y=0;
知识总结
例1、已知点 P( , ),在第三象限,则 的取值范围是( )
A、 B、 C、 D、
【解析】:第三象限的点的特征是横纵坐标都位负数,根据题意可用不等式进行解答
【答案】: ,A
第三象限:(-,-),则x<0,y<0;
例2:已知点 的坐标为(。
【解析】:根据横纵坐标的积等于正数可知两坐标同号,根据和为负数,可以知道两个坐标值都为负数。
【答案】:三
巩固练习:
1、若点 、三象限两坐标轴的角平分线上,则是( )
【解析】:根据点在一、三象限角平分线上的特点,可以知道点的横纵坐标值相等
【答案】:
知识点归纳
在象限的角平分线上的点的横纵坐标相等或者互为相反数
知识点三:平面直角坐标系内点的对称性、平移、旋转
例1、如图,线段 逆时针旋转90后,点至点,则点的坐标是( )
如果将绕原点顺时针旋转90后,点至点,则的坐标是( )
【解析】:过点
【答案】:B(-3,-1),C(3,1)
例2:在直角坐标平面内,已知正方形的顶点的坐标是,顶点是,则点的坐标是什么?
观察形式 ,想想以前学过的知识
【解析】:过分别向坐
标轴作垂线构造全等三角形
【答案】: C(5,2),D(3,5)
1.已知点A(3,-1)与点B关于原点对称,则点B的坐标为_______________。
2.经过点 (2,7)且垂直于 直线可表示为
3. 到距离为3的点所在的直线是 。
4. 已知点A(0,a),点B(1,0),直线AB与坐标轴围成的三角形面积为4,则a=_______________。
5. 点A(1+m,m)向上平移2个单位至点A’,若点A与A’恰好关于x轴对称,则点A’坐标是_____________。
6. 将点P(-3,y)向下平移3个单位,向左平移2个单位后得到点Q(x,-1),则xy=_______________。
(-3,1)
y=7
x=3或x=-3
8或-8
(0,1)
-10
7. 点P (2,3) 绕着原点O逆时针旋转90°后得到的点Q的坐标是 _______________。
8. 已知长方形ABCD中,AB=5,BC=8,并且AB∥x轴,若点A的坐标为(-2,4),则点C的坐标为_______________。
9. 已知平面直角坐标系中点P的纵坐标是2,且点P到y轴的距离是3,则点P的坐标为___________ ____。
直角坐标平面内,点直 两坐标轴围成的三角形的面积是6,则点的坐标是 _______________
(-3,2)
(3,12)
(3,2)或(-3,2)
(0,3)或(0,-3)
11.已知点A(-1,0)和点B(1,2),要在一个点,使得为等腰三角形,则满足这样条件的点P共有( )
A.2个 B.3个 C.4个 D.5个
12. 点 P (– 5,1 – t ) 与点Q (k,4) 关于原点对称,则 3k – 2 t 的值为 ( )
A、– 25 B、25 C、5 D、– 5
13. 点M (2 – a,a + 1)在第二象限,则a的取值范围是 ( )
A、a < 2 B、– 1 < a < 2 C、a > – 1 D、a > 2
14. 已知点 P (m + 1,– 1) 在第二、四象限的角平分线上,则 m的值为 ( )
A、1 B、0 C、– 1 D、– 2
C
C
D
B
15. 如图,写出各顶点的坐标,判断的形状,并求的面积?
答案:A(-8,3),B(-3,0),C(0,5),等腰直角三角形
16. 已知点,点为坐标原点,点为点,
线段旋转90。
(1)试在坐标平面内画、点的位置,并写出它们的坐标
(2)求的面积
答案:(1)B(-2,4),C(4,-2);(2)6
17. 已知亮点的坐标,如图所示,
(1)求的面积
(2)若点满足条件的点的坐标
答案:(1)8,
(2)(0,2)、(0,-2)
18. 如图,平行四边形ABCD的顶点A、B、C的坐标分别为 A(– 2,4)、 B (– 2,0)、C (4,– 1),求点D的坐标及平行四边形ABCD的面积
答案:D的坐标为(4,3),平行四边形ABCD的面积为24
19. 如图为风筝的图案.
(1)若原点用字母表示,写出图中点A,B,C的坐标
(2)试求(1)中风筝所覆盖的平面的面积.
答案:(1) A(0,7), B(-3,1),
C(-3,-1)
(2) 27
对比学习
20. 在平面直角坐标系中,一蚂蚁从原点 出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位.其行走路线如下图所示.
(1)填写下列各点的坐标:A4( , ),A8( , ),A12( , );
(2)写出点A4n的坐标(n是正整数);
(3)指出蚂蚁从点A100到点A101的移动方向.
认真思考,你最棒
1.直角坐标平面内,点 A 到x 轴的距离为2,到为3,则点A为( )
2.直角坐标平面内点 ,关于轴的对称的点在第四象限 ,则的
取值范围是 _______________
3.已知点向左平移4个单位到达点,点关于原点的对称点为
则点的坐标是_______________。
4.在平面直角坐标系中,点找一点,使得为顶点构成的三角形是等腰三角形,则这样的点有_______________个.
6.已知点A(-1,2)、B(-3,-2)、C(-1,-3)、D(0,1),画出四边形ABCD,并求其面积。
7.已知点A(2,3)与点B(2,0),在直角坐标平面内描出两点,画出以A、B为顶点的正方形,并写出另外两顶点的坐标。
8.如图,矩形的顶点 为坐标原点,点A 在轴上,点B的坐标为(2,1)
如果将矩形绕点旋转180°,旋转后的图形为矩形 OA1B1C1那么点B1 的坐标为_______________。.
9.如图,A,B的坐标为(2,0),(0,1)若将线段A B平移至 ,则的值为_______________。
10.在平面直角坐标系中,O是坐标原点,已知A点的坐标为(1,1),请你在坐标轴上找出点B,使△AOB为等腰三角形,则符合条件的点B共有_______________。
