人教新课标A版 选修3-1 第四讲 平面解析几何的产生二 笛卡儿坐标系 课件 19张PPT
文档属性
| 名称 | 人教新课标A版 选修3-1 第四讲 平面解析几何的产生二 笛卡儿坐标系 课件 19张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-22 21:45:07 | ||
图片预览






文档简介
(共19张PPT)
普通高中课程标准实验教科书数学 选修3-1
数学史选讲
第四讲第二节 笛卡尔坐标系
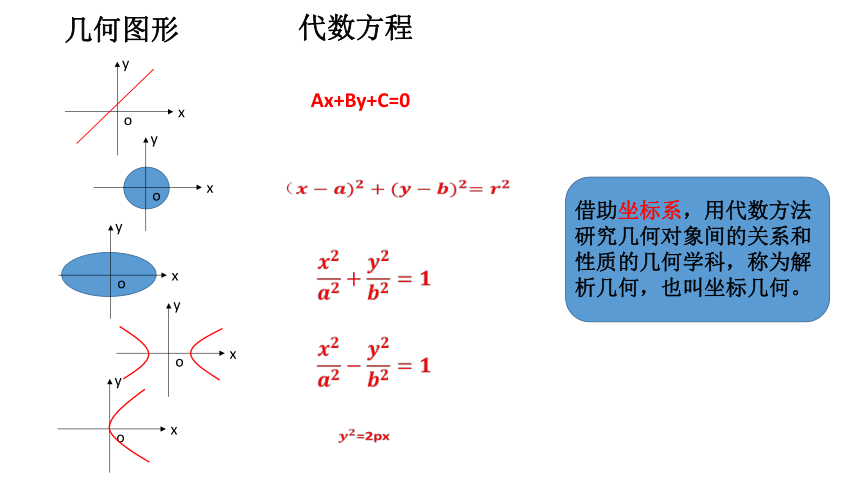
几何图形
代数方程
x
y
o
x
y
o
x
y
o
x
y
o
x
y
o
Ax+By+C=0
=2px
借助坐标系,用代数方法研究几何对象间的关系和性质的几何学科,称为解析几何,也叫坐标几何。
笛卡尔(1596-1650):哲学家、数学家,物理学家,解析几何的创始人。西方近代资产阶级哲学奠基人之一,其哲学与数学思想对历史有深远的影响。他出生在法国的一个上层社会家庭,父亲是地方法院的评议员,拥有一份相当可观的家业,从事这种与法律有关的职业的人在社会上有相当高的地位。因此,笛卡尔的一生都有可靠的经济来源,能够从事自己喜爱的事业。
一、笛卡尔简介
故事一 美丽的传说
笛卡尔于1596年出生在法国,欧洲大陆爆发黑死病时他流浪到瑞典,1649年,斯德哥尔摩的街头,52岁的笛卡尔邂逅了18岁的瑞典公主克里斯蒂娜。
几天后,他意外的接到通知,国王聘请他做小公主的数学老师。跟随前来通知的侍卫一起来到皇宫,他见到了街头偶遇的女孩子。
从此,他当上了小公主的数学老师。小公主的数学在笛卡尔的悉心指导下突飞猛进,笛卡尔向他介绍了自己研究的新领域——直角坐标系。每天形影不离的相处使他们彼此产生爱慕之心
公主的国王父亲知道后勃然大怒,下令将笛卡尔处死,小公主克里斯蒂娜苦苦哀求后,国王将其流放回法国,克里斯蒂娜也被父亲软禁起来
笛卡尔回法国后不久便染上重病,他日日给公主写信,因被国王拦截,克里斯蒂娜一直没收到笛卡尔的信。笛卡尔在给克里斯蒂娜寄出第十三封信后就气绝身亡了,这第十三封信的内容只有短短的一个公式:。国王看不懂,觉得他们俩之间并不是总是说情话的,将全城的数学家召集到皇宫,但没有一个人能解开,他不忍心看到心爱的女儿闷闷不乐,就把这封信交给了克里斯蒂娜。
公主看到后,立即明白了恋人的意图,她马上着手把方程的图形画出来,看到图形,她开心极了,她知道恋人仍然爱着她,原来方程的图形是一颗心的形状。这也就是著名的“心形线”。国王死后,克里斯蒂娜登基,立即派人在欧洲四处寻找心上人,无奈斯人已故,先她一步走了,徒留她孤零零在人间、、、、、、
真相:在历史上,笛卡尔和克里斯蒂娜的确有过交情。但笛卡尔是1649年10月4日应克里斯蒂娜邀请才来到瑞典,而当时克里斯蒂娜已成为了瑞典女王。笛卡尔与克里斯蒂娜谈论的主要是哲学问题而不是数学。笛卡尔真正的死因是因为天气寒冷加上过度操劳患上的肺炎,而不是黑死病。
我思故我在是笛卡尔最有名的哲学命题,出自《方法论》:
字面意思:我思想,所以意识到我的存在。
可以精炼的理解为:当我使用理性来思考的时候,我才真正获得了存在的价值。让真正的思考渗透进自己的人生,那么我的存在才有意义。
我思故我在
笛卡尔的《正确思维和发现科学真理的方法论》,简称《方法论》
笛卡尔在《方法论》中指出,研究问题的方法 四个步骤:
1、永远不接受任何我自己不清楚的真理,就是说要尽量避免鲁莽和偏见,只能是根据自己的判断非常清楚和确定,没有任何值得怀疑的地方的真理。就是说只要没有经过自己切身体会的问题,不管有什么权威的结论,都可以怀疑。这就是著名的“怀疑一切”理论。例如亚里士多德曾下结论说,女人比男人少两颗牙齿。但事实并非如此。
2、可以要将研究的复杂问题,尽量分解为多个比较简单的小问题,一个一个的分开解决。
3、将这个小问题从简单到复杂排列,先从容易解决的问题出手。
4、将所有问题解决后,再综合起来检验,看是否完全,是否将问题彻底解决了。
据说有一天,笛卡尔生病卧床,病情很重,尽管如此他还反复思考一个问题:几何图形是直观的,而代数方程是比较抽象的,能不能把几何图形和代数方程结合起来,也就是说能不能用几何图形来表示方程呢?要想达到此目的,关键是如何把组成几何图形的点和满足方程的每一组“数”挂上钩,他苦苦思索,拼命琢磨,通过什么样的方法,才能把“点”和“数”联系起来。突然,他看见屋顶角上的一只蜘蛛,拉着丝垂了下来。一会功夫,蜘蛛又顺这丝爬上去,在上边左右拉丝。蜘蛛的“表演”使笛卡尔的思路豁然开朗。他想,可以把蜘蛛看作一个点。他在屋子里可以上,下,左,右运动,能不能把蜘蛛的每一个位置用一组数确定下来呢?他又想,屋子里相邻的两面墙与地面交出了三条线,如果把地面上的墙角作为起点,把交出来的三条线作为三根数轴,那么空间中任意一点的位置就可以在这三根数轴上找到有顺序的三个数。反过来,任意给一组三个有顺序的数也可以在空间中找到一点P与之对应,同样道理,用一组数(X,Y)可以表示平面上的一个点,平面上的一个点也可以用一组两个有顺序的数来表示,这就是坐标系的雏形。
(其实笛卡尔坐标系是直角坐标系和斜角坐标系的统称)
二、笛卡尔坐标系
哲学方面:
欧洲近代哲学的要开拓者之一,黑格尔称他为“现代哲学之父”,他第一个创立了一套完整的哲学体系。
物理学方面:
在《屈光学》中首次对光的折射定律提出理论论证,解释彩虹现象。
在《哲学原理》中比较完整的第一次表述了惯性定律,第一次明确提出能量守恒定律。
天文学方面:
笛卡尔把他的机械论观点应用到天体,发展了宇宙演化论,形成了他关于宇宙发生与构造的学说。
三、笛卡尔的贡献
1637年:笛卡尔发表了他的著作《方法论》,后面有三篇附录:《折光学》《流星学》《几何学》
其中《几何学》共分三部分:
第一部分:讨论尺规作图
第二部分:讨论曲线的性质
第三部分:讨论立体和“超立体”的作图,但实际是当时流行的代数问题,讨论方程的根的性质。
后世的数学家把笛卡尔的《几何学》作为解析几何的起点。
数学方面:
在现代的数学文献中,有许多概念以笛卡尔的名字命名:笛卡尔坐标系、笛卡尔乘积、笛卡尔抛物线,等等。
从笛卡尔的《几何学》中可以看出,笛卡尔的中心思想是建立起一种“普遍”的数学,把算术、代数、几何统一起来。他设想,把任何数学问题化为一个代数问题,再把任何代数问题归结到去解一个方程式。为了实现上述的设想,笛卡尔从天文和地理的经纬制度出发,指出平面上的点和实数对(x,y)的对应关系。x ,y的不同数值可以确定平面上许多不同的点,这样就可以用代数的方法研究曲线的性质。
恩格斯高度评价说:“数学中的转折点笛卡尔的变数,有了变数,运动进入了数学,有了变数,微分与积分也就立即变称必须。”而他建立解析几何的成就在科学史上有划时代的意义。
数学史家克莱因这样评价笛卡尔:他只偶尔的是一个数学家,不过像他那样富于智力的人即使只花一部分时间在一个科目上,其工作也必定是有意义的。
在《几何学》中,笛卡尔充分发挥了代数学的强大威力,利用坐标系把代数和几何结合起来,使解析几何成为一种普遍的方法,从此数学一改古希腊以来依赖于几何学的局面,大大的向前迈进了一步。
1、有关笛卡尔的故事,哪一个故事让你感受最深?你从中得到什么启发?
2、笛卡尔《方法论》的思想与方法,对今后学习数学有什么启发?
四、学生活动
五、作业布置
网上搜索笛卡尔的其他相关事迹(比如三个奇特的梦、、、、、、)并分组制作笛卡尔小报
普通高中课程标准实验教科书数学 选修3-1
数学史选讲
第四讲第二节 笛卡尔坐标系
几何图形
代数方程
x
y
o
x
y
o
x
y
o
x
y
o
x
y
o
Ax+By+C=0
=2px
借助坐标系,用代数方法研究几何对象间的关系和性质的几何学科,称为解析几何,也叫坐标几何。
笛卡尔(1596-1650):哲学家、数学家,物理学家,解析几何的创始人。西方近代资产阶级哲学奠基人之一,其哲学与数学思想对历史有深远的影响。他出生在法国的一个上层社会家庭,父亲是地方法院的评议员,拥有一份相当可观的家业,从事这种与法律有关的职业的人在社会上有相当高的地位。因此,笛卡尔的一生都有可靠的经济来源,能够从事自己喜爱的事业。
一、笛卡尔简介
故事一 美丽的传说
笛卡尔于1596年出生在法国,欧洲大陆爆发黑死病时他流浪到瑞典,1649年,斯德哥尔摩的街头,52岁的笛卡尔邂逅了18岁的瑞典公主克里斯蒂娜。
几天后,他意外的接到通知,国王聘请他做小公主的数学老师。跟随前来通知的侍卫一起来到皇宫,他见到了街头偶遇的女孩子。
从此,他当上了小公主的数学老师。小公主的数学在笛卡尔的悉心指导下突飞猛进,笛卡尔向他介绍了自己研究的新领域——直角坐标系。每天形影不离的相处使他们彼此产生爱慕之心
公主的国王父亲知道后勃然大怒,下令将笛卡尔处死,小公主克里斯蒂娜苦苦哀求后,国王将其流放回法国,克里斯蒂娜也被父亲软禁起来
笛卡尔回法国后不久便染上重病,他日日给公主写信,因被国王拦截,克里斯蒂娜一直没收到笛卡尔的信。笛卡尔在给克里斯蒂娜寄出第十三封信后就气绝身亡了,这第十三封信的内容只有短短的一个公式:。国王看不懂,觉得他们俩之间并不是总是说情话的,将全城的数学家召集到皇宫,但没有一个人能解开,他不忍心看到心爱的女儿闷闷不乐,就把这封信交给了克里斯蒂娜。
公主看到后,立即明白了恋人的意图,她马上着手把方程的图形画出来,看到图形,她开心极了,她知道恋人仍然爱着她,原来方程的图形是一颗心的形状。这也就是著名的“心形线”。国王死后,克里斯蒂娜登基,立即派人在欧洲四处寻找心上人,无奈斯人已故,先她一步走了,徒留她孤零零在人间、、、、、、
真相:在历史上,笛卡尔和克里斯蒂娜的确有过交情。但笛卡尔是1649年10月4日应克里斯蒂娜邀请才来到瑞典,而当时克里斯蒂娜已成为了瑞典女王。笛卡尔与克里斯蒂娜谈论的主要是哲学问题而不是数学。笛卡尔真正的死因是因为天气寒冷加上过度操劳患上的肺炎,而不是黑死病。
我思故我在是笛卡尔最有名的哲学命题,出自《方法论》:
字面意思:我思想,所以意识到我的存在。
可以精炼的理解为:当我使用理性来思考的时候,我才真正获得了存在的价值。让真正的思考渗透进自己的人生,那么我的存在才有意义。
我思故我在
笛卡尔的《正确思维和发现科学真理的方法论》,简称《方法论》
笛卡尔在《方法论》中指出,研究问题的方法 四个步骤:
1、永远不接受任何我自己不清楚的真理,就是说要尽量避免鲁莽和偏见,只能是根据自己的判断非常清楚和确定,没有任何值得怀疑的地方的真理。就是说只要没有经过自己切身体会的问题,不管有什么权威的结论,都可以怀疑。这就是著名的“怀疑一切”理论。例如亚里士多德曾下结论说,女人比男人少两颗牙齿。但事实并非如此。
2、可以要将研究的复杂问题,尽量分解为多个比较简单的小问题,一个一个的分开解决。
3、将这个小问题从简单到复杂排列,先从容易解决的问题出手。
4、将所有问题解决后,再综合起来检验,看是否完全,是否将问题彻底解决了。
据说有一天,笛卡尔生病卧床,病情很重,尽管如此他还反复思考一个问题:几何图形是直观的,而代数方程是比较抽象的,能不能把几何图形和代数方程结合起来,也就是说能不能用几何图形来表示方程呢?要想达到此目的,关键是如何把组成几何图形的点和满足方程的每一组“数”挂上钩,他苦苦思索,拼命琢磨,通过什么样的方法,才能把“点”和“数”联系起来。突然,他看见屋顶角上的一只蜘蛛,拉着丝垂了下来。一会功夫,蜘蛛又顺这丝爬上去,在上边左右拉丝。蜘蛛的“表演”使笛卡尔的思路豁然开朗。他想,可以把蜘蛛看作一个点。他在屋子里可以上,下,左,右运动,能不能把蜘蛛的每一个位置用一组数确定下来呢?他又想,屋子里相邻的两面墙与地面交出了三条线,如果把地面上的墙角作为起点,把交出来的三条线作为三根数轴,那么空间中任意一点的位置就可以在这三根数轴上找到有顺序的三个数。反过来,任意给一组三个有顺序的数也可以在空间中找到一点P与之对应,同样道理,用一组数(X,Y)可以表示平面上的一个点,平面上的一个点也可以用一组两个有顺序的数来表示,这就是坐标系的雏形。
(其实笛卡尔坐标系是直角坐标系和斜角坐标系的统称)
二、笛卡尔坐标系
哲学方面:
欧洲近代哲学的要开拓者之一,黑格尔称他为“现代哲学之父”,他第一个创立了一套完整的哲学体系。
物理学方面:
在《屈光学》中首次对光的折射定律提出理论论证,解释彩虹现象。
在《哲学原理》中比较完整的第一次表述了惯性定律,第一次明确提出能量守恒定律。
天文学方面:
笛卡尔把他的机械论观点应用到天体,发展了宇宙演化论,形成了他关于宇宙发生与构造的学说。
三、笛卡尔的贡献
1637年:笛卡尔发表了他的著作《方法论》,后面有三篇附录:《折光学》《流星学》《几何学》
其中《几何学》共分三部分:
第一部分:讨论尺规作图
第二部分:讨论曲线的性质
第三部分:讨论立体和“超立体”的作图,但实际是当时流行的代数问题,讨论方程的根的性质。
后世的数学家把笛卡尔的《几何学》作为解析几何的起点。
数学方面:
在现代的数学文献中,有许多概念以笛卡尔的名字命名:笛卡尔坐标系、笛卡尔乘积、笛卡尔抛物线,等等。
从笛卡尔的《几何学》中可以看出,笛卡尔的中心思想是建立起一种“普遍”的数学,把算术、代数、几何统一起来。他设想,把任何数学问题化为一个代数问题,再把任何代数问题归结到去解一个方程式。为了实现上述的设想,笛卡尔从天文和地理的经纬制度出发,指出平面上的点和实数对(x,y)的对应关系。x ,y的不同数值可以确定平面上许多不同的点,这样就可以用代数的方法研究曲线的性质。
恩格斯高度评价说:“数学中的转折点笛卡尔的变数,有了变数,运动进入了数学,有了变数,微分与积分也就立即变称必须。”而他建立解析几何的成就在科学史上有划时代的意义。
数学史家克莱因这样评价笛卡尔:他只偶尔的是一个数学家,不过像他那样富于智力的人即使只花一部分时间在一个科目上,其工作也必定是有意义的。
在《几何学》中,笛卡尔充分发挥了代数学的强大威力,利用坐标系把代数和几何结合起来,使解析几何成为一种普遍的方法,从此数学一改古希腊以来依赖于几何学的局面,大大的向前迈进了一步。
1、有关笛卡尔的故事,哪一个故事让你感受最深?你从中得到什么启发?
2、笛卡尔《方法论》的思想与方法,对今后学习数学有什么启发?
四、学生活动
五、作业布置
网上搜索笛卡尔的其他相关事迹(比如三个奇特的梦、、、、、、)并分组制作笛卡尔小报
同课章节目录
- 第一讲 早期的算术与几何
- 一 古埃及的数学
- 二 两河流域的数学
- 三 丰富多彩的记数制度
- 第二讲 古希腊数学
- 一 希腊数学的先行者
- 二 毕达哥拉斯学派
- 三 欧几里得与《原本》
- 四 数学之神──阿基米德
- 第三讲 中国古代数学瑰宝
- 一 《周髀算经》与赵爽弦图
- 二 《九章算术》
- 三 大衍求一术
- 四 中国古代数学家
- 第四讲 平面解析几何的产生
- 一 坐标思想的早期萌芽
- 二 笛卡儿坐标系
- 三 费马的解析几何思想
- 四 解析几何的进一步发展
- 第五讲 微积分的诞生
- 一 微积分产生的历史背景
- 二 科学巨人牛顿的工作
- 三 莱布尼茨的“微积分”
- 第六讲 近代数学两巨星
- 一 分析的化身──欧拉
- 二 数学王子──高斯
- 第七讲 千古谜题
- 一 三次、四次方程求根公式的发现
- 二 高次方程可解性问题的解决
- 三 伽罗瓦与群论
- 四 古希腊三大几何问题的解决
- 第八讲 对无穷的深入思考
- 一 古代的无穷观念
- 二 无穷集合论的创立
- 三 集合论的进一步发展与完善
- 第九讲 中国现代数学的开拓与发展
- 一 中国现代数学发展概观
- 二 人民的数学家──华罗庚
- 三 当代几何大师──陈省身
