人教新课标A版 选修3-1 第二讲 古希腊数学三 欧几里得与《原本》 课件 35张PPT
文档属性
| 名称 | 人教新课标A版 选修3-1 第二讲 古希腊数学三 欧几里得与《原本》 课件 35张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 668.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-22 00:00:00 | ||
图片预览










文档简介
(共35张PPT)
欧几里得与
《几何原本》
思考:请回忆一下,我们当初是 怎么学习几何的?
几何命题的明晰性和可靠性
爱因斯坦说:“一个人当他最初接近几何时,如果不曾为它的明晰性和可靠性所感动,那么他是不会成为一个科学家的。”
《几何原本》
拉丁文版
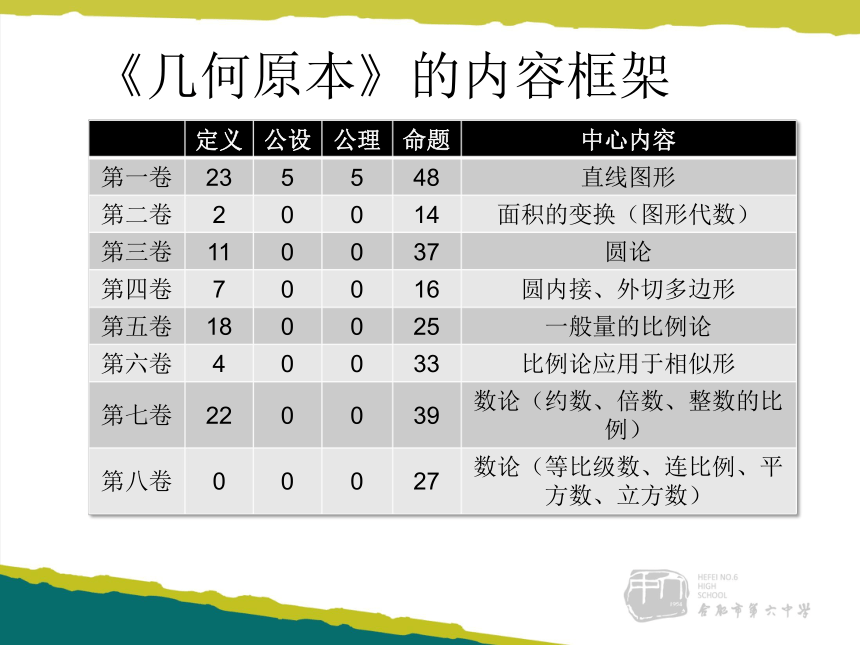
《几何原本》的内容框架
定义 公设 公理 命题 中心内容
第一卷 23 5 5 48 直线图形
第二卷 2 0 0 14 面积的变换(图形代数)
第三卷 11 0 0 37 圆论
第四卷 7 0 0 16 圆内接、外切多边形
第五卷 18 0 0 25 一般量的比例论
第六卷 4 0 0 33 比例论应用于相似形
第七卷 22 0 0 39 数论(约数、倍数、整数的比例)
第八卷 0 0 0 27 数论(等比级数、连比例、平方数、立方数)
定义 公设 公理 命题 中心内容
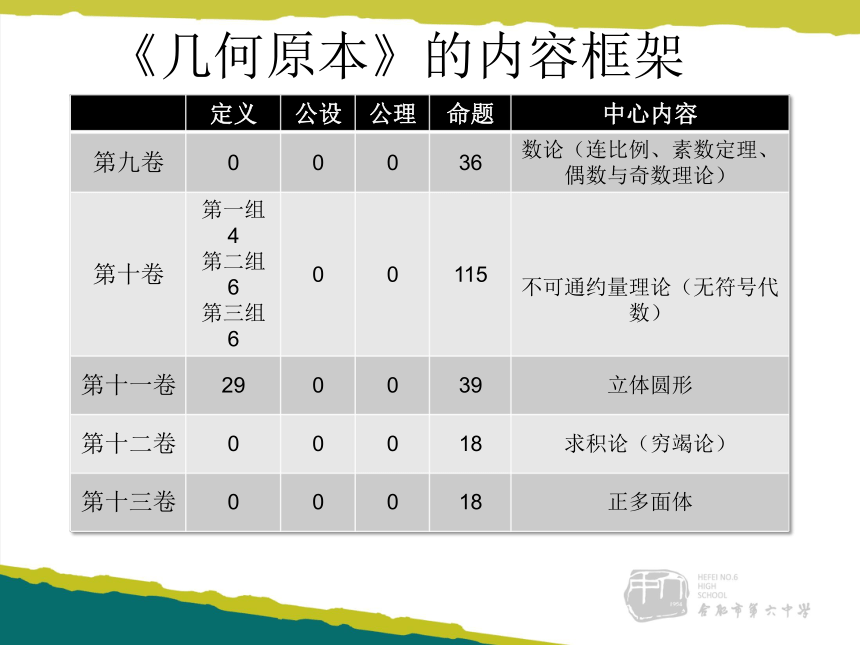
第九卷 0 0 0 36 数论(连比例、素数定理、偶数与奇数理论)
第十卷 第一组
4
第二组
6
第三组
6 0 0 115 不可通约量理论(无符号代数)
第十一卷 29 0 0 39 立体圆形
第十二卷 0 0 0 18 求积论(穷竭论)
第十三卷 0 0 0 18 正多面体
《几何原本》的内容框架
《几何原本》的内容
初中学的几何知识全部出自这本书的前六卷:
点、线、面、角的概念、三角形、两条直线的位置关系、四边形、圆、相似形、求图形的面积。
《几何原本》的最大价值
这种范式要求一门学科中的每一个命题必须是在它之前已建立的一些命题基础上的逻辑结论,而所有这样的推理链的共同出发点,是一些基本定义和被认为是不证自明的基本原理——公设或公理,这就是所谓的“公理化思想”。
《几何原本》的最大价值
就像一个个零散的部件在欧几里得这里形成了一个完整的体系系统;
就像一颗颗散落的珍珠被串成了一条项链。
《几何原本》完成了这一艰巨的任务。
自此,“数学从一门经验的科学变成了一门完全理智的科学”。
《几何原本》的第Ⅰ卷
23个定义:
1.点是没有部分的东西。
2.线只有长度而没有宽度。
3.一线的两端是点。
4.直线是它上面的点一样地平放着的线。
5.面只有长度和宽度。
6.面的边缘是线。
7.平面是它上面的线一样地平放着的面。
8.平面角是在一平面内但不在一条直线上的两条相交线相互的倾斜度。
《几何原本》的第Ⅰ卷
23个定义:
9.当包含角的两条线都是直线时,这个角叫做直线角。
10.当一条直线和另一条直线交成邻角彼此相等时,这些角每一个被叫做直角,而且称这一条直线垂直于另一条直线。
11.大于直角的角称为钝角。
12.小于直角的角称为锐角。
13.边界是物体的边缘。
《几何原本》的第Ⅰ卷
23个定义:
14.图形是一个边界或者几个边界所围成的。
15.圆:由一条线包围着的平面图形,其内有一点与这条线上任何一个点所连成的线段都相等。
16.这个点(指定义15中提到的那个点)叫做圆心。
17.圆的直径是任意一条经过圆心的直线在两个方向被圆截得的线段,且把圆二等分。
《几何原本》的第Ⅰ卷
23个定义:
18.半圆是直径与被它切割的圆弧所围成的图形,半圆的圆心与原圆心相同。(暂无注释)
19.直线形是由直线围成的.三边形是由三条直线围成的,四边形是由四条直线围成的,多边形是由四条以上直线围成的。
20.在三边形中,三条边相等的,叫做等边三角形;只有两条边相等的,叫做等腰三角形;各边不等的,叫做不等边三角形。
《几何原本》的第Ⅰ卷
23个定义:
21.此外,在三边形中,有一个角是直角的,叫做直角三角形;有一个角是钝角的,叫做钝角三角形;各边不等的,叫做不等边三角形。
《几何原本》的第Ⅰ卷
23个定义:
22.在四边形中,四边相等且四个角是直角的,叫做正方形;角是直角,但四边不全相等的,叫做长方形;四边相等,但角不是直角的,叫做菱形;对角相等且对边相等,但边不全相等且角不是直角的,叫做斜方形;其余的四边形叫做不规则四边形。
23.平行直线是在同一个平面内向两端无限延长不能相交的直线。
《几何原本》的第Ⅰ卷
5条公设:
1.过两点能作且只能作一直线。
2.线段(有限直线)可以无限地延长。
3.以任一点为圆心,任意长为半径,可作一圆。
4.凡是直角都相等。
5.同平面内一条直线和另外两条直线相交,若在直线同侧的两个内角之和小于180°,则这两条直线经无限延长后在这一侧一定相交。
《几何原本》的第Ⅰ卷
5条公理:
1.等于同量的量彼此相等。
2.等量加等量,其和相等。
3.等量减等量,其差相等。
4.彼此能重合的物体是全等的;
5.整体大于部分。
近代数学不区分公设,公理,统一称为公理。
《几何原本》中的命题
过程:设此线段为AB,以A为圆心,AB为半径作圆BCD(公设3:以任一点为圆心,任意长为半径,可作一圆),
再以B为圆心,AB为半径作圆ACE(公设3:以任一点为圆心,任意长为半径,可作一圆),
再由二圆的交点C到A、B作直线段AC、BC(公设1:过两点能作且只能作一直线).由于A是圆BCD的圆心,所以AB=AC(定义15:圆:由一条线包围着的平面图形,其内有一点与这条线上任何一个点所连成的线段都相等).
同理AB=BC,所以BC=AC(公理1:等于同量的量彼此相等).
这样,△ABC的三边相等,因而是等边三角形。(定义20:在三边形中,三条边相等的,叫做等边三角形
命题1:在一给定的有限长线段上作一等边三角形.
《几何原本》中的命题
过程:设A是已知点,BC是已知线段。由点A到点B连线段AB(公设1:过两点能作且只能作一直线),
而且在AB上作等边三角形DAB[1.1:在一给定的有限长线段上作一等边三角形],
延长DA、DB成直线AE、BF(公设2:线段(有限直线)可以无限地延长).以B为心,以BC为距离画圆CGH(公设3:以任一点为圆心,任意长为半径,可作一圆).再以D为心,以DG为距离画圆GKL(公设3)因为点B是圆CGH的心,故BC等于BG(定义15),点D是圆GKL的心,故DL等于DG(定义15),又DA等于DB,所以余量AL等于余量BG(公理3:等量减等量,其差相等)
命题2:由一个已知点(作为端点)作一线段等于已知线段.
《几何原本》中的命题
过程:但已证明了BC等于BG,所以线段AL、BC的每一个都等于BG.(公理1)
一又因等于同量的量彼此相等(公理1)
所以AL也等于BC
从而,由已知点A作出了线段AL等于已知线段BC.
命题2:由一个已知点(作为端点)作一线段等于已知线段.
《几何原本》中的命题
欧几里得惊人的天才首先在于他恰好选择了他所必需的公理、公设和定义,既不太多,又足够证明全书所含有的一切定理;其次在于,到那时为止所知道的几何命题全部被合乎逻辑地编排起来,成为体系。这是十分伟大的业绩。代表着人类理性思维的一个高峰。
牛顿的《自然哲学数学原理》就是按照《几何原本》的标准样式写的。
“几何之父”欧几里得
一件是他生活在公元前300年左右,居于柏拉图的学生与阿基米德之间,
另一件是他曾在亚历山大港教过书。
“几何之父”欧几里得
科学史家萨顿曾经感慨过:
“对欧几里得以及其他某些先贤生平的这种无知是寻常而非例外的,人们记住了暴君和独裁者,成功的政治人物,富豪(起码一部分富豪),却忘记了自己最大的恩人。”
萨顿
“几何之父”欧几里得
故事一:
《希腊数学史》记载:有个学生跟欧几里得刚刚学了第一个几何命题,便急不可耐地问学了几何学将得到什么好处,欧几里得对侍者说:拿三个钱来给这位先生,他想的是在学习中要得到实惠。
“几何之父”欧几里得
故事二:
另一位古代学者在《几何原本》注释中写道:
托勒密国王很热爱几何,但是又不想深入研究,就问欧几里得:学习几何学有没有捷径可走?欧几里得答道:几何学没有陛下的坦途。(几何无王者之道/几何无坦途)
总结
《几何原本》对世界数学的贡献:
建立了欧氏几何;建立了公理演绎体系,即用公理、公设和定义的推证方法,确立了数学的基本方法学;将逻辑证明系统地引入数学中,确立了逻辑学的基本方法。
总结
《几何原本》对世界的影响:
从此西方的科学里有了体系一说,西方的科学家们惊叹于欧几里得发明的这套方法,于是纷纷将这一套东西引入到自己的研究领域,从此这种方式成为了西方科学研究的基本范式。
任何人研究一个全新的领域,都先作几个最基本的假设作为公理,然后从这些假设出发推导出一些定理,当然,必须保证自己推导的这些定理前后不矛盾(这就需要很强的逻辑能力,《几何原本》就是对逻辑能力最好的训练材料),然后以这些推导出来的定理为基础,利用严密的逻辑一步步的扩大领域,最终把这个领域内的一切都包含进来。如果公理可靠,那么推出来的结论也一定是可靠的。
总结
后世评价:
徐光启:
“此书有四不必:不必疑,不必揣,不必试,不必改。”
“此书无一人不当学”
“能精此书者,无一事不可精,好学此书者,无一事不可学。”
总结
后世评价:
爱因斯坦:
“世界第一次目睹了一个逻辑体系的奇迹。这个逻辑体系如此精密地一步一步地推进,以致它的每一个命题都是绝对不容置疑的——我这里说的是欧几里得几何,推理的这种可赞叹的胜利,使人类理智获得了为取得以后的成就所必须的信心。”
总结
后世评价:
19世纪的英国数学家奥古斯塔斯·德·摩根所言:
“从来不曾有过,并且在亲眼见到之前我们也绝不该相信,会有任何值得一提的几何体系,包含任何与欧几里得所定方案有偏差的材料。”
总结
启发:
请同学们畅所欲言,说说你的感受。
“几何无坦途”
学习无坦途
与君共勉
谢谢大家!
欧几里得与
《几何原本》
思考:请回忆一下,我们当初是 怎么学习几何的?
几何命题的明晰性和可靠性
爱因斯坦说:“一个人当他最初接近几何时,如果不曾为它的明晰性和可靠性所感动,那么他是不会成为一个科学家的。”
《几何原本》
拉丁文版
《几何原本》的内容框架
定义 公设 公理 命题 中心内容
第一卷 23 5 5 48 直线图形
第二卷 2 0 0 14 面积的变换(图形代数)
第三卷 11 0 0 37 圆论
第四卷 7 0 0 16 圆内接、外切多边形
第五卷 18 0 0 25 一般量的比例论
第六卷 4 0 0 33 比例论应用于相似形
第七卷 22 0 0 39 数论(约数、倍数、整数的比例)
第八卷 0 0 0 27 数论(等比级数、连比例、平方数、立方数)
定义 公设 公理 命题 中心内容
第九卷 0 0 0 36 数论(连比例、素数定理、偶数与奇数理论)
第十卷 第一组
4
第二组
6
第三组
6 0 0 115 不可通约量理论(无符号代数)
第十一卷 29 0 0 39 立体圆形
第十二卷 0 0 0 18 求积论(穷竭论)
第十三卷 0 0 0 18 正多面体
《几何原本》的内容框架
《几何原本》的内容
初中学的几何知识全部出自这本书的前六卷:
点、线、面、角的概念、三角形、两条直线的位置关系、四边形、圆、相似形、求图形的面积。
《几何原本》的最大价值
这种范式要求一门学科中的每一个命题必须是在它之前已建立的一些命题基础上的逻辑结论,而所有这样的推理链的共同出发点,是一些基本定义和被认为是不证自明的基本原理——公设或公理,这就是所谓的“公理化思想”。
《几何原本》的最大价值
就像一个个零散的部件在欧几里得这里形成了一个完整的体系系统;
就像一颗颗散落的珍珠被串成了一条项链。
《几何原本》完成了这一艰巨的任务。
自此,“数学从一门经验的科学变成了一门完全理智的科学”。
《几何原本》的第Ⅰ卷
23个定义:
1.点是没有部分的东西。
2.线只有长度而没有宽度。
3.一线的两端是点。
4.直线是它上面的点一样地平放着的线。
5.面只有长度和宽度。
6.面的边缘是线。
7.平面是它上面的线一样地平放着的面。
8.平面角是在一平面内但不在一条直线上的两条相交线相互的倾斜度。
《几何原本》的第Ⅰ卷
23个定义:
9.当包含角的两条线都是直线时,这个角叫做直线角。
10.当一条直线和另一条直线交成邻角彼此相等时,这些角每一个被叫做直角,而且称这一条直线垂直于另一条直线。
11.大于直角的角称为钝角。
12.小于直角的角称为锐角。
13.边界是物体的边缘。
《几何原本》的第Ⅰ卷
23个定义:
14.图形是一个边界或者几个边界所围成的。
15.圆:由一条线包围着的平面图形,其内有一点与这条线上任何一个点所连成的线段都相等。
16.这个点(指定义15中提到的那个点)叫做圆心。
17.圆的直径是任意一条经过圆心的直线在两个方向被圆截得的线段,且把圆二等分。
《几何原本》的第Ⅰ卷
23个定义:
18.半圆是直径与被它切割的圆弧所围成的图形,半圆的圆心与原圆心相同。(暂无注释)
19.直线形是由直线围成的.三边形是由三条直线围成的,四边形是由四条直线围成的,多边形是由四条以上直线围成的。
20.在三边形中,三条边相等的,叫做等边三角形;只有两条边相等的,叫做等腰三角形;各边不等的,叫做不等边三角形。
《几何原本》的第Ⅰ卷
23个定义:
21.此外,在三边形中,有一个角是直角的,叫做直角三角形;有一个角是钝角的,叫做钝角三角形;各边不等的,叫做不等边三角形。
《几何原本》的第Ⅰ卷
23个定义:
22.在四边形中,四边相等且四个角是直角的,叫做正方形;角是直角,但四边不全相等的,叫做长方形;四边相等,但角不是直角的,叫做菱形;对角相等且对边相等,但边不全相等且角不是直角的,叫做斜方形;其余的四边形叫做不规则四边形。
23.平行直线是在同一个平面内向两端无限延长不能相交的直线。
《几何原本》的第Ⅰ卷
5条公设:
1.过两点能作且只能作一直线。
2.线段(有限直线)可以无限地延长。
3.以任一点为圆心,任意长为半径,可作一圆。
4.凡是直角都相等。
5.同平面内一条直线和另外两条直线相交,若在直线同侧的两个内角之和小于180°,则这两条直线经无限延长后在这一侧一定相交。
《几何原本》的第Ⅰ卷
5条公理:
1.等于同量的量彼此相等。
2.等量加等量,其和相等。
3.等量减等量,其差相等。
4.彼此能重合的物体是全等的;
5.整体大于部分。
近代数学不区分公设,公理,统一称为公理。
《几何原本》中的命题
过程:设此线段为AB,以A为圆心,AB为半径作圆BCD(公设3:以任一点为圆心,任意长为半径,可作一圆),
再以B为圆心,AB为半径作圆ACE(公设3:以任一点为圆心,任意长为半径,可作一圆),
再由二圆的交点C到A、B作直线段AC、BC(公设1:过两点能作且只能作一直线).由于A是圆BCD的圆心,所以AB=AC(定义15:圆:由一条线包围着的平面图形,其内有一点与这条线上任何一个点所连成的线段都相等).
同理AB=BC,所以BC=AC(公理1:等于同量的量彼此相等).
这样,△ABC的三边相等,因而是等边三角形。(定义20:在三边形中,三条边相等的,叫做等边三角形
命题1:在一给定的有限长线段上作一等边三角形.
《几何原本》中的命题
过程:设A是已知点,BC是已知线段。由点A到点B连线段AB(公设1:过两点能作且只能作一直线),
而且在AB上作等边三角形DAB[1.1:在一给定的有限长线段上作一等边三角形],
延长DA、DB成直线AE、BF(公设2:线段(有限直线)可以无限地延长).以B为心,以BC为距离画圆CGH(公设3:以任一点为圆心,任意长为半径,可作一圆).再以D为心,以DG为距离画圆GKL(公设3)因为点B是圆CGH的心,故BC等于BG(定义15),点D是圆GKL的心,故DL等于DG(定义15),又DA等于DB,所以余量AL等于余量BG(公理3:等量减等量,其差相等)
命题2:由一个已知点(作为端点)作一线段等于已知线段.
《几何原本》中的命题
过程:但已证明了BC等于BG,所以线段AL、BC的每一个都等于BG.(公理1)
一又因等于同量的量彼此相等(公理1)
所以AL也等于BC
从而,由已知点A作出了线段AL等于已知线段BC.
命题2:由一个已知点(作为端点)作一线段等于已知线段.
《几何原本》中的命题
欧几里得惊人的天才首先在于他恰好选择了他所必需的公理、公设和定义,既不太多,又足够证明全书所含有的一切定理;其次在于,到那时为止所知道的几何命题全部被合乎逻辑地编排起来,成为体系。这是十分伟大的业绩。代表着人类理性思维的一个高峰。
牛顿的《自然哲学数学原理》就是按照《几何原本》的标准样式写的。
“几何之父”欧几里得
一件是他生活在公元前300年左右,居于柏拉图的学生与阿基米德之间,
另一件是他曾在亚历山大港教过书。
“几何之父”欧几里得
科学史家萨顿曾经感慨过:
“对欧几里得以及其他某些先贤生平的这种无知是寻常而非例外的,人们记住了暴君和独裁者,成功的政治人物,富豪(起码一部分富豪),却忘记了自己最大的恩人。”
萨顿
“几何之父”欧几里得
故事一:
《希腊数学史》记载:有个学生跟欧几里得刚刚学了第一个几何命题,便急不可耐地问学了几何学将得到什么好处,欧几里得对侍者说:拿三个钱来给这位先生,他想的是在学习中要得到实惠。
“几何之父”欧几里得
故事二:
另一位古代学者在《几何原本》注释中写道:
托勒密国王很热爱几何,但是又不想深入研究,就问欧几里得:学习几何学有没有捷径可走?欧几里得答道:几何学没有陛下的坦途。(几何无王者之道/几何无坦途)
总结
《几何原本》对世界数学的贡献:
建立了欧氏几何;建立了公理演绎体系,即用公理、公设和定义的推证方法,确立了数学的基本方法学;将逻辑证明系统地引入数学中,确立了逻辑学的基本方法。
总结
《几何原本》对世界的影响:
从此西方的科学里有了体系一说,西方的科学家们惊叹于欧几里得发明的这套方法,于是纷纷将这一套东西引入到自己的研究领域,从此这种方式成为了西方科学研究的基本范式。
任何人研究一个全新的领域,都先作几个最基本的假设作为公理,然后从这些假设出发推导出一些定理,当然,必须保证自己推导的这些定理前后不矛盾(这就需要很强的逻辑能力,《几何原本》就是对逻辑能力最好的训练材料),然后以这些推导出来的定理为基础,利用严密的逻辑一步步的扩大领域,最终把这个领域内的一切都包含进来。如果公理可靠,那么推出来的结论也一定是可靠的。
总结
后世评价:
徐光启:
“此书有四不必:不必疑,不必揣,不必试,不必改。”
“此书无一人不当学”
“能精此书者,无一事不可精,好学此书者,无一事不可学。”
总结
后世评价:
爱因斯坦:
“世界第一次目睹了一个逻辑体系的奇迹。这个逻辑体系如此精密地一步一步地推进,以致它的每一个命题都是绝对不容置疑的——我这里说的是欧几里得几何,推理的这种可赞叹的胜利,使人类理智获得了为取得以后的成就所必须的信心。”
总结
后世评价:
19世纪的英国数学家奥古斯塔斯·德·摩根所言:
“从来不曾有过,并且在亲眼见到之前我们也绝不该相信,会有任何值得一提的几何体系,包含任何与欧几里得所定方案有偏差的材料。”
总结
启发:
请同学们畅所欲言,说说你的感受。
“几何无坦途”
学习无坦途
与君共勉
谢谢大家!
同课章节目录
- 第一讲 早期的算术与几何
- 一 古埃及的数学
- 二 两河流域的数学
- 三 丰富多彩的记数制度
- 第二讲 古希腊数学
- 一 希腊数学的先行者
- 二 毕达哥拉斯学派
- 三 欧几里得与《原本》
- 四 数学之神──阿基米德
- 第三讲 中国古代数学瑰宝
- 一 《周髀算经》与赵爽弦图
- 二 《九章算术》
- 三 大衍求一术
- 四 中国古代数学家
- 第四讲 平面解析几何的产生
- 一 坐标思想的早期萌芽
- 二 笛卡儿坐标系
- 三 费马的解析几何思想
- 四 解析几何的进一步发展
- 第五讲 微积分的诞生
- 一 微积分产生的历史背景
- 二 科学巨人牛顿的工作
- 三 莱布尼茨的“微积分”
- 第六讲 近代数学两巨星
- 一 分析的化身──欧拉
- 二 数学王子──高斯
- 第七讲 千古谜题
- 一 三次、四次方程求根公式的发现
- 二 高次方程可解性问题的解决
- 三 伽罗瓦与群论
- 四 古希腊三大几何问题的解决
- 第八讲 对无穷的深入思考
- 一 古代的无穷观念
- 二 无穷集合论的创立
- 三 集合论的进一步发展与完善
- 第九讲 中国现代数学的开拓与发展
- 一 中国现代数学发展概观
- 二 人民的数学家──华罗庚
- 三 当代几何大师──陈省身
