人教新课标A版 选修3-1 第二讲 古希腊数学四 数学之神──阿基米德 课件 21张PPT
文档属性
| 名称 | 人教新课标A版 选修3-1 第二讲 古希腊数学四 数学之神──阿基米德 课件 21张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-22 21:59:19 | ||
图片预览







文档简介
(共21张PPT)
数学史
探索数学概念、理论诞生的源头
发现数学发展历史每个不平凡的段落
追寻它的发展轨迹
去认识一位位杰出的科学家
见证学科发展中的重要事件
感悟数学文化的真谛
数学之神——阿基米德
阿基米德
阿基米德(公元前287-前212),古希腊最著名的数学家和发明家。出生于意大利西西里岛的叙拉古,早年曾在“智慧之都”亚历山大跟过欧几里得的学生学习,并在以后与那里的师友保持着密切联系 ,他的许多成果都是通过与亚历山大学者的通信而保存下来。阿基米德的著述极为丰富,涉及数学、力学及天文学等。
从以阿基米德为代表的亚历山大里亚的数学家开始,算术和代数开始成为一门独立的数学学科。
(1)第一个提出圆的周长、圆面积、扇形面积计算的
准确公式。
(2)比较精确的计算了圆周率(223 / 71<π<22 / 7)。
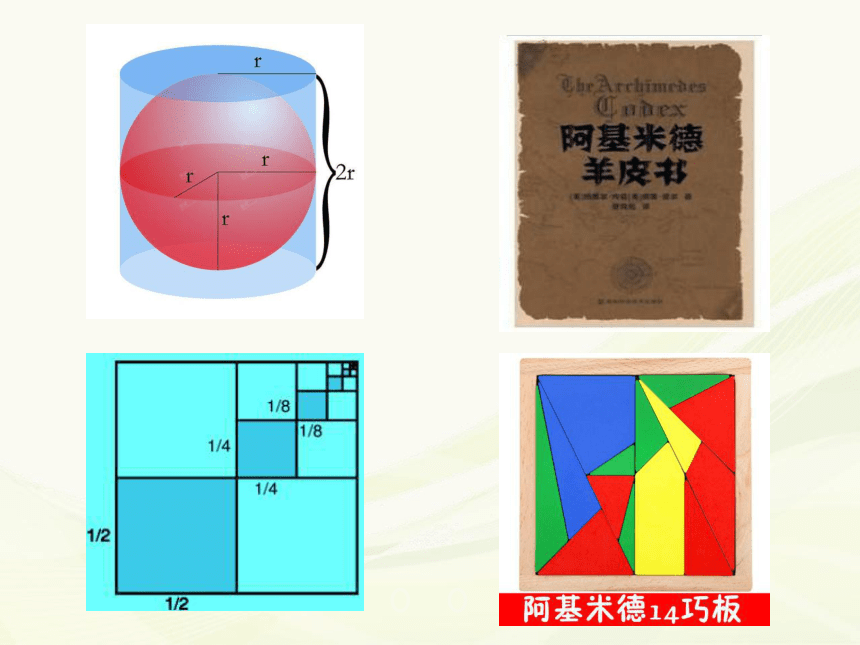
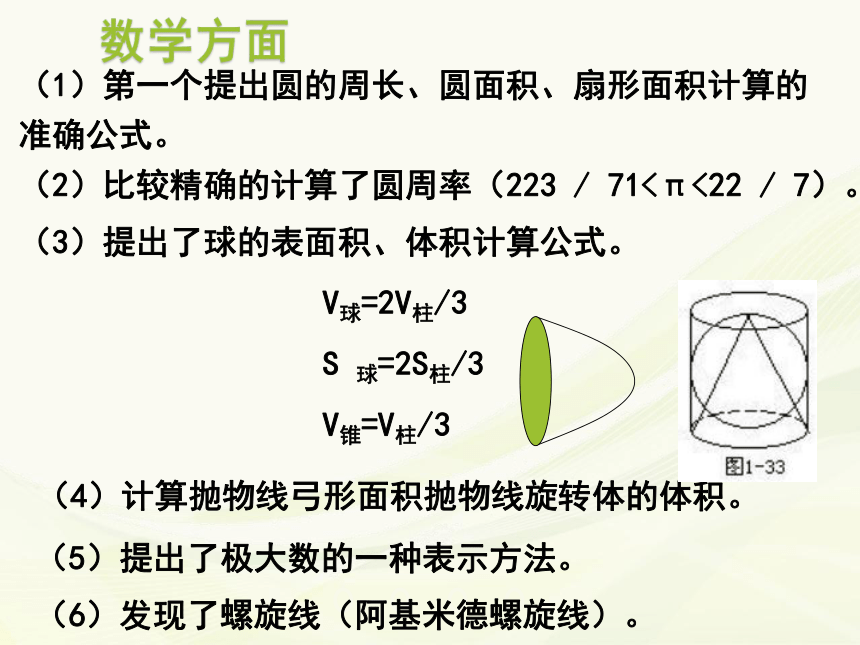
(3)提出了球的表面积、体积计算公式。
V球=2V柱/3
S 球=2S柱/3
V锥=V柱/3
(4)计算抛物线弓形面积抛物线旋转体的体积。
(5)提出了极大数的一种表示方法。
(6)发现了螺旋线(阿基米德螺旋线)。
数学方面
活动1:古今中外,许多人致力于 的研究与计算。为了越来越精确地计算出 的近似值,一代代的数学家为了这个神秘数的贡献了无数的时间与心血。古人计算 一般是用“割圆法”。阿基米德用正96边形得到 223 / 71<π<22 / 7;刘徽用正3072边形得到其近似值 ;又过了大约200年,祖冲之(429-500)得到了其有理数近似值 ;而在欧洲,直到1585年才发现了这个有理数近似值。这种基于几何的算法计算量大,需要顽强的毅力和高超的技巧,因而也显示了当时的数学发展水平。
(1)请你说说圆周率的意义。
(2)为什么 ?请你说说道理。
爱像圆周率,无限不循环
阿基米德求圆周率的方法及其近似值对此后的欧洲和阿拉伯文明有长期的影响。我们将这种方法称为阿基米德—刘徽方法。其中多边形不断增多边数就是对圆周无限细分,由许多三角形的总和来求圆周长及面积就是无限求和。
微积分的萌芽
《给埃拉托斯特尼的信》:内容是探讨解决力学问题的方法。这是1906年丹麦语言学家J.L.海贝格在土耳其伊斯坦布尔发现的一卷羊皮纸手稿,后来以《阿基米德方法》为名刊行于世。它主要讲根据力学原理去发现问题的方法。他把一块面积或体积看成是有重量的东西,分成许多非常小的长条或薄片,然后用已知面积或体积去平衡这些“元素”,找到了重心和支点,所求的面积或体积就可以用杠杆定律计算出来。他把这种方法看作是严格证明前的一种试探性工作,得到结果以后,还要用归谬法去证明它。
一起来玩跷跷板
“穷竭法”与“平衡法”
穷竭法是安蒂丰首先使用,并被古希腊数学家普遍用来证明面积和体积的方法。穷竭法可以用来严格证明已经猜想出来的命题,但不能用来发现新的结果。
阿基米德发明了求面积和体积的“平衡法”,求出面积或体积后再用“穷竭法”加以证明。阿基米德“平衡法”与“穷竭法”的结合是严格证明与创造技巧相结合的典范。
活动2:如图,AC平行于x轴,过点A作抛物线的切线交y轴于N,欧几里得已在《二次曲线》中证明得到MO=ON,作CE平行MN交直线AO于F.延长AF至R,使FA=FR.
探究:CF与EF的长度关系
对话阿基米德
活动3:设弧ABC为抛物线弓形,D为AB的中点,DC为平行抛物线轴的直线且交抛物线弓形弧于C,又E,F分别是BC,AC的中点,且过这两点平行于抛物线轴的直线EH,FG分别交抛物线弓形弧于H,G,试证
巧妙几何达无限
他巧妙地运用几何方法解决了这一问题。
将一个边长为1的正方形分割为如下所示的无数的L形块,每个深色块均占其所在的L形块面积的三分之一。这些深色正方形块的面积即是所求级数的各项。
将运动观点引入数学
阿基米德螺线:是指平面上一条射线绕它的固定端点匀速旋转,同时有一点从端点出发沿直线匀速运动,则点P的轨迹称为“阿基米德螺线”。从物理的角度来说,阿基米德螺线是匀速直线运动和匀速圆周运动的合成,如右图:
《论螺线》:阿基米德明确了螺线的定义,以及对螺线的面积的计算方法。“第一面积”等于“第一圆”面积的三分之一。
向大师致敬
美国的E.T.贝尔在《数学人物》上是这样评价阿基米德的:“任何一张开列有史以来三个最伟大的数学家的名单之中,必定会包括阿基米德,而另外两个通常是牛顿和高斯。不过以他们的宏伟业绩和所处的时代背景来比较,或拿他们影响当代和后世的深邃久远来比较,还应首推阿基米德。”阿基米德是数学家与力学家的伟大学者,他的几何著作是希腊数学的顶峰。
向大师致敬
阿基米德完全掌握了在他之前的古希腊数学的精华,并且作出了进一步的完善和发展。这里包括他提出的“阿基米德公理”,使在与极限有关命题证明中的“穷竭法”更加严密,运用自如,完成了圆面积、球面积和体积的计算公式的证明,他在做出微积分方面的成果时的严格性远远超过了后来的牛顿与莱布尼茨。
阿基米德的工作远超出了欧几里得《原本》中的研究范围。通过对古希腊三大几何问题的深入研究,在螺线、圆锥曲线和圆锥线旋转体方面,在三次方程和算术方面,都作出了贡献。
向大师致敬
阿基米德是将数学和物理结合研究的最早典范。他用公理化方法奠定了理论力学和流体静力学的基础,是力学的创始人。他还将数学和力学用于实际,发明了许多实用机械。
谢谢大家!
数学史
探索数学概念、理论诞生的源头
发现数学发展历史每个不平凡的段落
追寻它的发展轨迹
去认识一位位杰出的科学家
见证学科发展中的重要事件
感悟数学文化的真谛
数学之神——阿基米德
阿基米德
阿基米德(公元前287-前212),古希腊最著名的数学家和发明家。出生于意大利西西里岛的叙拉古,早年曾在“智慧之都”亚历山大跟过欧几里得的学生学习,并在以后与那里的师友保持着密切联系 ,他的许多成果都是通过与亚历山大学者的通信而保存下来。阿基米德的著述极为丰富,涉及数学、力学及天文学等。
从以阿基米德为代表的亚历山大里亚的数学家开始,算术和代数开始成为一门独立的数学学科。
(1)第一个提出圆的周长、圆面积、扇形面积计算的
准确公式。
(2)比较精确的计算了圆周率(223 / 71<π<22 / 7)。
(3)提出了球的表面积、体积计算公式。
V球=2V柱/3
S 球=2S柱/3
V锥=V柱/3
(4)计算抛物线弓形面积抛物线旋转体的体积。
(5)提出了极大数的一种表示方法。
(6)发现了螺旋线(阿基米德螺旋线)。
数学方面
活动1:古今中外,许多人致力于 的研究与计算。为了越来越精确地计算出 的近似值,一代代的数学家为了这个神秘数的贡献了无数的时间与心血。古人计算 一般是用“割圆法”。阿基米德用正96边形得到 223 / 71<π<22 / 7;刘徽用正3072边形得到其近似值 ;又过了大约200年,祖冲之(429-500)得到了其有理数近似值 ;而在欧洲,直到1585年才发现了这个有理数近似值。这种基于几何的算法计算量大,需要顽强的毅力和高超的技巧,因而也显示了当时的数学发展水平。
(1)请你说说圆周率的意义。
(2)为什么 ?请你说说道理。
爱像圆周率,无限不循环
阿基米德求圆周率的方法及其近似值对此后的欧洲和阿拉伯文明有长期的影响。我们将这种方法称为阿基米德—刘徽方法。其中多边形不断增多边数就是对圆周无限细分,由许多三角形的总和来求圆周长及面积就是无限求和。
微积分的萌芽
《给埃拉托斯特尼的信》:内容是探讨解决力学问题的方法。这是1906年丹麦语言学家J.L.海贝格在土耳其伊斯坦布尔发现的一卷羊皮纸手稿,后来以《阿基米德方法》为名刊行于世。它主要讲根据力学原理去发现问题的方法。他把一块面积或体积看成是有重量的东西,分成许多非常小的长条或薄片,然后用已知面积或体积去平衡这些“元素”,找到了重心和支点,所求的面积或体积就可以用杠杆定律计算出来。他把这种方法看作是严格证明前的一种试探性工作,得到结果以后,还要用归谬法去证明它。
一起来玩跷跷板
“穷竭法”与“平衡法”
穷竭法是安蒂丰首先使用,并被古希腊数学家普遍用来证明面积和体积的方法。穷竭法可以用来严格证明已经猜想出来的命题,但不能用来发现新的结果。
阿基米德发明了求面积和体积的“平衡法”,求出面积或体积后再用“穷竭法”加以证明。阿基米德“平衡法”与“穷竭法”的结合是严格证明与创造技巧相结合的典范。
活动2:如图,AC平行于x轴,过点A作抛物线的切线交y轴于N,欧几里得已在《二次曲线》中证明得到MO=ON,作CE平行MN交直线AO于F.延长AF至R,使FA=FR.
探究:CF与EF的长度关系
对话阿基米德
活动3:设弧ABC为抛物线弓形,D为AB的中点,DC为平行抛物线轴的直线且交抛物线弓形弧于C,又E,F分别是BC,AC的中点,且过这两点平行于抛物线轴的直线EH,FG分别交抛物线弓形弧于H,G,试证
巧妙几何达无限
他巧妙地运用几何方法解决了这一问题。
将一个边长为1的正方形分割为如下所示的无数的L形块,每个深色块均占其所在的L形块面积的三分之一。这些深色正方形块的面积即是所求级数的各项。
将运动观点引入数学
阿基米德螺线:是指平面上一条射线绕它的固定端点匀速旋转,同时有一点从端点出发沿直线匀速运动,则点P的轨迹称为“阿基米德螺线”。从物理的角度来说,阿基米德螺线是匀速直线运动和匀速圆周运动的合成,如右图:
《论螺线》:阿基米德明确了螺线的定义,以及对螺线的面积的计算方法。“第一面积”等于“第一圆”面积的三分之一。
向大师致敬
美国的E.T.贝尔在《数学人物》上是这样评价阿基米德的:“任何一张开列有史以来三个最伟大的数学家的名单之中,必定会包括阿基米德,而另外两个通常是牛顿和高斯。不过以他们的宏伟业绩和所处的时代背景来比较,或拿他们影响当代和后世的深邃久远来比较,还应首推阿基米德。”阿基米德是数学家与力学家的伟大学者,他的几何著作是希腊数学的顶峰。
向大师致敬
阿基米德完全掌握了在他之前的古希腊数学的精华,并且作出了进一步的完善和发展。这里包括他提出的“阿基米德公理”,使在与极限有关命题证明中的“穷竭法”更加严密,运用自如,完成了圆面积、球面积和体积的计算公式的证明,他在做出微积分方面的成果时的严格性远远超过了后来的牛顿与莱布尼茨。
阿基米德的工作远超出了欧几里得《原本》中的研究范围。通过对古希腊三大几何问题的深入研究,在螺线、圆锥曲线和圆锥线旋转体方面,在三次方程和算术方面,都作出了贡献。
向大师致敬
阿基米德是将数学和物理结合研究的最早典范。他用公理化方法奠定了理论力学和流体静力学的基础,是力学的创始人。他还将数学和力学用于实际,发明了许多实用机械。
谢谢大家!
同课章节目录
- 第一讲 早期的算术与几何
- 一 古埃及的数学
- 二 两河流域的数学
- 三 丰富多彩的记数制度
- 第二讲 古希腊数学
- 一 希腊数学的先行者
- 二 毕达哥拉斯学派
- 三 欧几里得与《原本》
- 四 数学之神──阿基米德
- 第三讲 中国古代数学瑰宝
- 一 《周髀算经》与赵爽弦图
- 二 《九章算术》
- 三 大衍求一术
- 四 中国古代数学家
- 第四讲 平面解析几何的产生
- 一 坐标思想的早期萌芽
- 二 笛卡儿坐标系
- 三 费马的解析几何思想
- 四 解析几何的进一步发展
- 第五讲 微积分的诞生
- 一 微积分产生的历史背景
- 二 科学巨人牛顿的工作
- 三 莱布尼茨的“微积分”
- 第六讲 近代数学两巨星
- 一 分析的化身──欧拉
- 二 数学王子──高斯
- 第七讲 千古谜题
- 一 三次、四次方程求根公式的发现
- 二 高次方程可解性问题的解决
- 三 伽罗瓦与群论
- 四 古希腊三大几何问题的解决
- 第八讲 对无穷的深入思考
- 一 古代的无穷观念
- 二 无穷集合论的创立
- 三 集合论的进一步发展与完善
- 第九讲 中国现代数学的开拓与发展
- 一 中国现代数学发展概观
- 二 人民的数学家──华罗庚
- 三 当代几何大师──陈省身
