人教新课标A版 选修3-1 第三讲 中国古代数学瑰宝四 中国古代数学家 课件 18张PPT
文档属性
| 名称 | 人教新课标A版 选修3-1 第三讲 中国古代数学瑰宝四 中国古代数学家 课件 18张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-22 00:00:00 | ||
图片预览




文档简介
(共18张PPT)
人教A版 选修3-1 数学史选讲
第三讲 中国古代数学瑰宝
中国古代数学家
谈一谈
你所了解的中国古代数学家
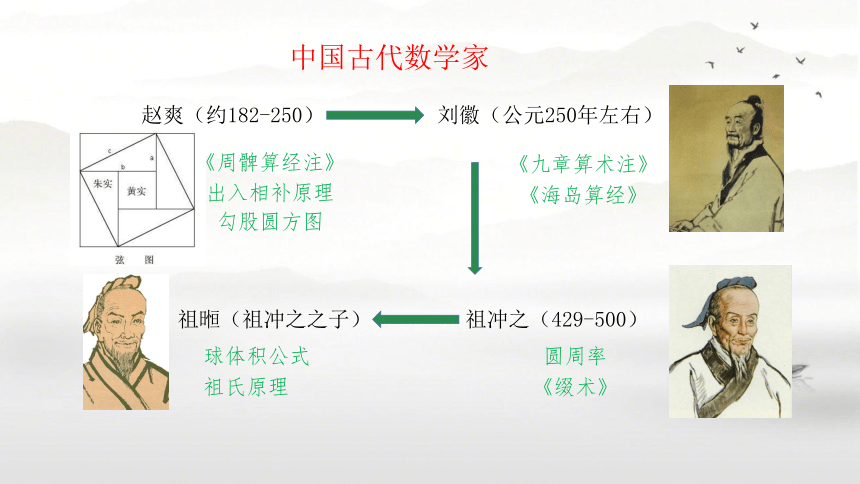
中国古代数学家
赵爽(约182-250)
《周髀算经注》
出入相补原理
勾股圆方图
刘徽(公元250年左右)
《九章算术注》
《海岛算经》
祖冲之(429-500)
圆周率
《缀术》
祖暅(祖冲之之子)
球体积公式
祖氏原理
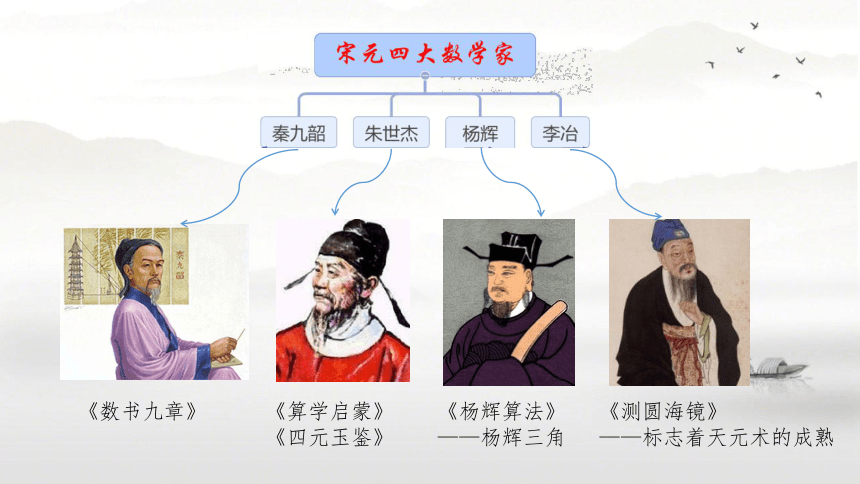
《数书九章》
《算学启蒙》
《四元玉鉴》
《杨辉算法》
——杨辉三角
《测圆海镜》
——标志着天元术的成熟
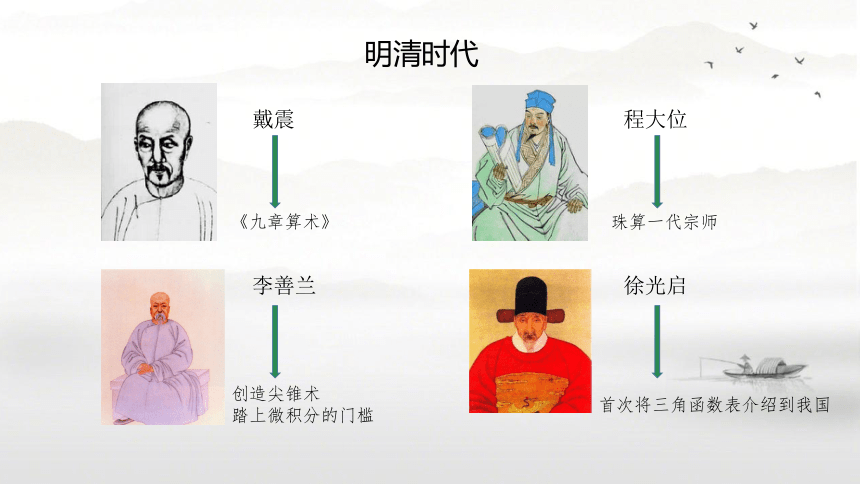
明清时代
戴震
《九章算术》
程大位
珠算一代宗师
李善兰
创造尖锥术
踏上微积分的门槛
徐光启
首次将三角函数表介绍到我国
汉族,山东邹平市人,魏晋期间伟大的数学家,中国古典数学理论的奠基人之一。是中国数学史上一个非常伟大的数学家,他的杰作《九章算术注》和《海岛算经》,是中国最宝贵的数学遗产。
刘徽割圆术的基本思想是——
“割之弥细,所失弥少,割之又割以至于不可割,则与圆合体而无所失矣”
就是说分割越细,误差就越小,无限细分就能逐步接近圆周率的实际值。
圆的内接正6边形
圆的内接正192边形
徽率
------极限思想、积分思想的萌芽.
“当边数无限增加时,圆内接正多边形的面积趋近于圆的面积。”
公元前5世纪,希腊数学家安蒂丰最早发现这个结论,称其为“穷竭法”。
随后,公元3世纪,阿基米德利用圆周长介于圆内接正多边形周长和圆外切正多边形周长之间的事实算出 .
而刘徽用割圆术计算圆周率只需要用圆内接正多边形.
——事半功倍
刘徽发现《九章算术》中的球体积公式是错误的,为了正确计算球的体积,他创造了一个新的立体图形——“牟合方盖”。
球体与牟合方盖的体积之比为
1.祖冲之算出了圆周率的上下极限:
2.密率------ (又称为祖率)
约率------
3.《缀术》
子承父业
利用截面原理“幂势既同,则积不容异.”
------后世称为“祖暅原理”、“祖氏原理”
牟合方盖的体积
刘徽的球体积与牟合方盖体积之比
一次由两名同学来参加“喜羊羊运动会”
------判断题,每题5秒钟时间,在5秒内可更改答案,看谁先到达终点。
与同学分享,认识这些中国古代数学家之后,你有哪些体会?
热爱数学文化 学习前人精神
百折不挠 勇于开拓
谢谢!
人教A版 选修3-1 数学史选讲
第三讲 中国古代数学瑰宝
中国古代数学家
谈一谈
你所了解的中国古代数学家
中国古代数学家
赵爽(约182-250)
《周髀算经注》
出入相补原理
勾股圆方图
刘徽(公元250年左右)
《九章算术注》
《海岛算经》
祖冲之(429-500)
圆周率
《缀术》
祖暅(祖冲之之子)
球体积公式
祖氏原理
《数书九章》
《算学启蒙》
《四元玉鉴》
《杨辉算法》
——杨辉三角
《测圆海镜》
——标志着天元术的成熟
明清时代
戴震
《九章算术》
程大位
珠算一代宗师
李善兰
创造尖锥术
踏上微积分的门槛
徐光启
首次将三角函数表介绍到我国
汉族,山东邹平市人,魏晋期间伟大的数学家,中国古典数学理论的奠基人之一。是中国数学史上一个非常伟大的数学家,他的杰作《九章算术注》和《海岛算经》,是中国最宝贵的数学遗产。
刘徽割圆术的基本思想是——
“割之弥细,所失弥少,割之又割以至于不可割,则与圆合体而无所失矣”
就是说分割越细,误差就越小,无限细分就能逐步接近圆周率的实际值。
圆的内接正6边形
圆的内接正192边形
徽率
------极限思想、积分思想的萌芽.
“当边数无限增加时,圆内接正多边形的面积趋近于圆的面积。”
公元前5世纪,希腊数学家安蒂丰最早发现这个结论,称其为“穷竭法”。
随后,公元3世纪,阿基米德利用圆周长介于圆内接正多边形周长和圆外切正多边形周长之间的事实算出 .
而刘徽用割圆术计算圆周率只需要用圆内接正多边形.
——事半功倍
刘徽发现《九章算术》中的球体积公式是错误的,为了正确计算球的体积,他创造了一个新的立体图形——“牟合方盖”。
球体与牟合方盖的体积之比为
1.祖冲之算出了圆周率的上下极限:
2.密率------ (又称为祖率)
约率------
3.《缀术》
子承父业
利用截面原理“幂势既同,则积不容异.”
------后世称为“祖暅原理”、“祖氏原理”
牟合方盖的体积
刘徽的球体积与牟合方盖体积之比
一次由两名同学来参加“喜羊羊运动会”
------判断题,每题5秒钟时间,在5秒内可更改答案,看谁先到达终点。
与同学分享,认识这些中国古代数学家之后,你有哪些体会?
热爱数学文化 学习前人精神
百折不挠 勇于开拓
谢谢!
同课章节目录
- 第一讲 早期的算术与几何
- 一 古埃及的数学
- 二 两河流域的数学
- 三 丰富多彩的记数制度
- 第二讲 古希腊数学
- 一 希腊数学的先行者
- 二 毕达哥拉斯学派
- 三 欧几里得与《原本》
- 四 数学之神──阿基米德
- 第三讲 中国古代数学瑰宝
- 一 《周髀算经》与赵爽弦图
- 二 《九章算术》
- 三 大衍求一术
- 四 中国古代数学家
- 第四讲 平面解析几何的产生
- 一 坐标思想的早期萌芽
- 二 笛卡儿坐标系
- 三 费马的解析几何思想
- 四 解析几何的进一步发展
- 第五讲 微积分的诞生
- 一 微积分产生的历史背景
- 二 科学巨人牛顿的工作
- 三 莱布尼茨的“微积分”
- 第六讲 近代数学两巨星
- 一 分析的化身──欧拉
- 二 数学王子──高斯
- 第七讲 千古谜题
- 一 三次、四次方程求根公式的发现
- 二 高次方程可解性问题的解决
- 三 伽罗瓦与群论
- 四 古希腊三大几何问题的解决
- 第八讲 对无穷的深入思考
- 一 古代的无穷观念
- 二 无穷集合论的创立
- 三 集合论的进一步发展与完善
- 第九讲 中国现代数学的开拓与发展
- 一 中国现代数学发展概观
- 二 人民的数学家──华罗庚
- 三 当代几何大师──陈省身
