人教新课标A版 选修3-1 第一讲 早期的算术与几何一 古埃及的数学 课件 共29张PPT
文档属性
| 名称 | 人教新课标A版 选修3-1 第一讲 早期的算术与几何一 古埃及的数学 课件 共29张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-22 22:16:41 | ||
图片预览






文档简介
(共29张PPT)
数学的起源
早期的算术和几何
思考
早期的数学起源于哪里?
它有哪些用处?
讨论并回答
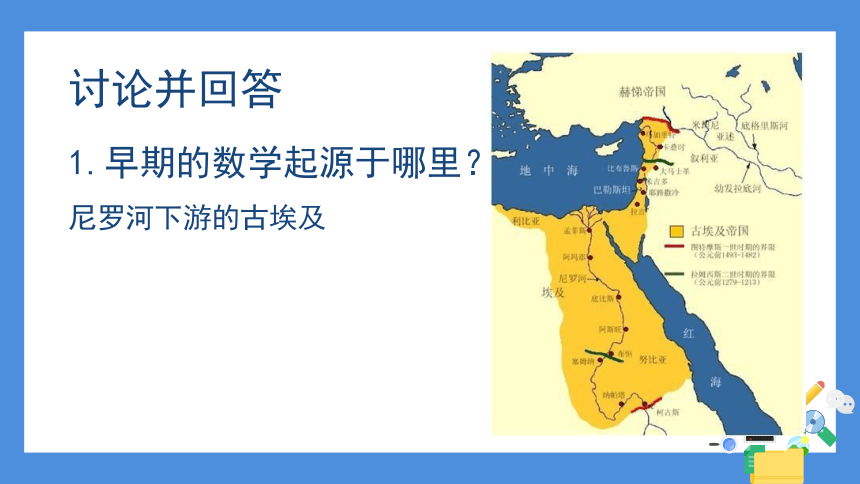
1.早期的数学起源于哪里?
尼罗河下游的古埃及
讨论并回答
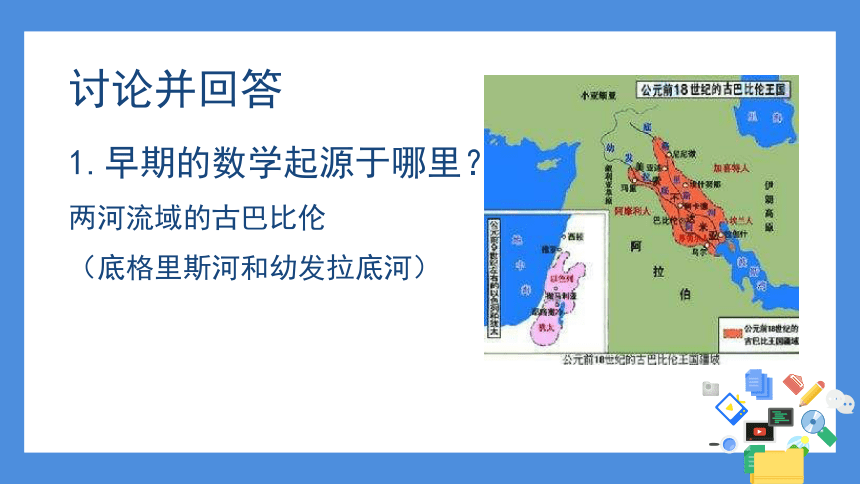
1.早期的数学起源于哪里?
两河流域的古巴比伦
(底格里斯河和幼发拉底河)
讨论并回答
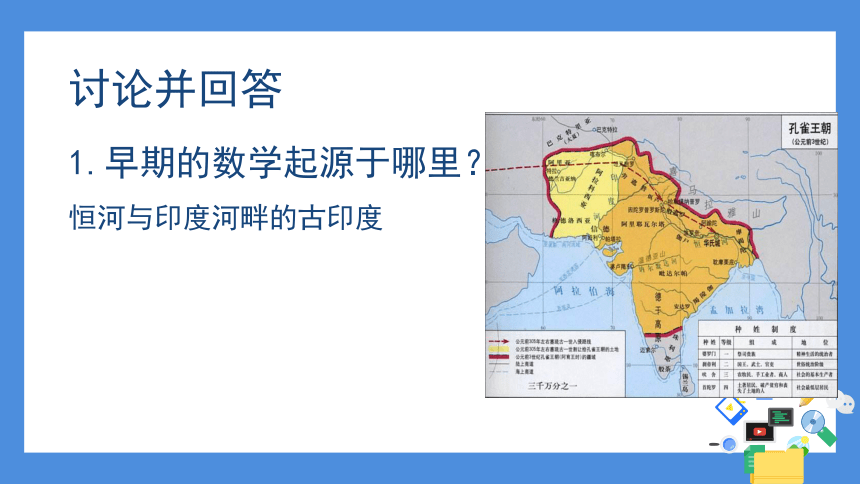
1.早期的数学起源于哪里?
恒河与印度河畔的古印度
讨论并回答
1.早期的数学起源于哪里?
黄河与长江流域的古代中国
整体分布
古埃及的数学
01
时间节点
古埃及位于非洲东北部的尼罗河两岸。
公元前525年,波斯入侵,埃及成为波斯帝国的一个郡;
公元前332年以后,该地区处于希腊人的统治之下,归为希腊数学;
古埃及数学指的是公元前6世纪以前的数学。
1.象形文字中的数字记法
你会用古埃及的数字
符号去表示12345?
这样的记数方法有什
么弊端呢?
分数及分数符号的产生(青铜时代后)
埃及分数是指分子是1的分数,也叫单位分数。古代埃及人在进行分数运算时,只使用分子是1的分数。因此这种分数也叫做埃及分数,或者叫单分数。
书写方式
2.纸草书上的数学
在尼罗河三角洲地区盛产一种“芦苇”的水生植物——纸草,用颜料蘸取练习。
一本是“莱茵德纸草书”,归伦敦大英博物馆;公元前1650年;(更重要),84个问题
另一本是“莫斯科纸草书”,在莫斯科国立造型艺术博物馆;公元前1850年,25个问题
莱茵德纸草书
准确的计算,阐明一切黑暗的、秘密存在的事物的指南
例:七个房间,每个房间里有七只猫,每只猫抓七只老鼠,每只老鼠要吃掉七穗谷物,每穗谷物若被播种,能收获七加仑粮食(一加仑粮食算一件东西),请问本题中提及的东西的总数量。
答案:19607
莱茵德纸草书
2.单分数
埃及数学中的独特现象:分数都写成若干个单分数的和的形式(除特例)
偏爱成为不解之谜;
两个面包均分给五个人;
2.单分数
当9个面包要平均分给 10个人的时候,古埃及人不知道每个人可以取得 9/10,而是说每人 ,受到大家的吐槽;
1/3+1/4+1/5+1/12+1/30
阿基米德这样的数学巨匠,也研究过埃及分数。沃尔夫数学奖得主,保罗-欧德斯,他提出了著名的猜想 4/n=1/x+1/y+1/z(1948)(n>1), 难倒了世界上第一流的数学家。
奇妙的传说
老人弥留之际,将家中11匹马分给3个儿子,老大1/2,老二1/4,老三1/6。二分之一是5匹半马,总不能把马杀了吧,正在无奈之际,邻居把自己家的马牵来,老大二分之一,牵走了6匹;老二四分之一,牵走了3匹;老三六分之一,牵走了2匹。一共11匹,分完后,邻居把自己的马牵了回去。即11/12=1/2+1/4+1/6。
3、算术运算
僧侣文的记数方法属于分级符号制,整数的加减法很简单,把相应的符号累计起来,再转化为相应的符号即可。分数不容易,因为需要转化为单分数
乘法(累加法)
补充:其他的记数制度
分级符号制:古希腊的字母记数法,犹太民族的希伯来字母计数法和阿拉伯字母记数法
补充:其他的记数制度
简单累数制:古埃及的象形文字;巴比伦的楔形文中,60以下的数采用简单累数制;罗马数字(I,V)
补充:其他的记数制度
乘法累数制:中国数字
4600不必写成“千千千千百百百百百百”
4.代数问题和几何问题
1、书中有几个问题属于现代代数的一元一次方程问题:一个量,加上自身的七分之一等于19.现代解法很简单,但是纸草书中解法很难,但是答案却是正确的。
2、给出了一些求面积和体积的题,得到的结果不够精确。尽管埃及是几何学的发源地,但是几何水平不高。
3.几何学的诞生
尼罗河是埃及的母亲河,拉绳者面积测量
数学科学最早在埃及兴起,因为那里的祭司才有足够的闲暇
实验阶段,几何知识是零碎的,片段的,直到希腊人占领这儿。
二、古巴比伦的数学
早在公元前四五千年,两河流域的苏美尔人用削尖的芦苇杆在泥板上写字,晒干后泥板书,字形像楔子,叫做楔形字。
1、楔形文字中的记数法
记数方法:10进制和60进制混用
简单累数制
2.泥板上的代数
代数和算术的区别(未知数、符号、方程)
现藏在耶鲁大学的泥板上:两个数的积为60,差为7(求根公式)
巴比伦人会求解指数方程
例:有一笔钱,年利率为20%,多长时间本金和利息一样多
3.泥板上的几何
古印度也有记载,在《测绳的法规》中提到
3.泥板上的几何
纽约哥伦比亚大学的真本图书馆内有一块公元前1900—_公元前1600的泥板,称为普林顿322号数学泥板
THANKS
数学的起源
早期的算术和几何
思考
早期的数学起源于哪里?
它有哪些用处?
讨论并回答
1.早期的数学起源于哪里?
尼罗河下游的古埃及
讨论并回答
1.早期的数学起源于哪里?
两河流域的古巴比伦
(底格里斯河和幼发拉底河)
讨论并回答
1.早期的数学起源于哪里?
恒河与印度河畔的古印度
讨论并回答
1.早期的数学起源于哪里?
黄河与长江流域的古代中国
整体分布
古埃及的数学
01
时间节点
古埃及位于非洲东北部的尼罗河两岸。
公元前525年,波斯入侵,埃及成为波斯帝国的一个郡;
公元前332年以后,该地区处于希腊人的统治之下,归为希腊数学;
古埃及数学指的是公元前6世纪以前的数学。
1.象形文字中的数字记法
你会用古埃及的数字
符号去表示12345?
这样的记数方法有什
么弊端呢?
分数及分数符号的产生(青铜时代后)
埃及分数是指分子是1的分数,也叫单位分数。古代埃及人在进行分数运算时,只使用分子是1的分数。因此这种分数也叫做埃及分数,或者叫单分数。
书写方式
2.纸草书上的数学
在尼罗河三角洲地区盛产一种“芦苇”的水生植物——纸草,用颜料蘸取练习。
一本是“莱茵德纸草书”,归伦敦大英博物馆;公元前1650年;(更重要),84个问题
另一本是“莫斯科纸草书”,在莫斯科国立造型艺术博物馆;公元前1850年,25个问题
莱茵德纸草书
准确的计算,阐明一切黑暗的、秘密存在的事物的指南
例:七个房间,每个房间里有七只猫,每只猫抓七只老鼠,每只老鼠要吃掉七穗谷物,每穗谷物若被播种,能收获七加仑粮食(一加仑粮食算一件东西),请问本题中提及的东西的总数量。
答案:19607
莱茵德纸草书
2.单分数
埃及数学中的独特现象:分数都写成若干个单分数的和的形式(除特例)
偏爱成为不解之谜;
两个面包均分给五个人;
2.单分数
当9个面包要平均分给 10个人的时候,古埃及人不知道每个人可以取得 9/10,而是说每人 ,受到大家的吐槽;
1/3+1/4+1/5+1/12+1/30
阿基米德这样的数学巨匠,也研究过埃及分数。沃尔夫数学奖得主,保罗-欧德斯,他提出了著名的猜想 4/n=1/x+1/y+1/z(1948)(n>1), 难倒了世界上第一流的数学家。
奇妙的传说
老人弥留之际,将家中11匹马分给3个儿子,老大1/2,老二1/4,老三1/6。二分之一是5匹半马,总不能把马杀了吧,正在无奈之际,邻居把自己家的马牵来,老大二分之一,牵走了6匹;老二四分之一,牵走了3匹;老三六分之一,牵走了2匹。一共11匹,分完后,邻居把自己的马牵了回去。即11/12=1/2+1/4+1/6。
3、算术运算
僧侣文的记数方法属于分级符号制,整数的加减法很简单,把相应的符号累计起来,再转化为相应的符号即可。分数不容易,因为需要转化为单分数
乘法(累加法)
补充:其他的记数制度
分级符号制:古希腊的字母记数法,犹太民族的希伯来字母计数法和阿拉伯字母记数法
补充:其他的记数制度
简单累数制:古埃及的象形文字;巴比伦的楔形文中,60以下的数采用简单累数制;罗马数字(I,V)
补充:其他的记数制度
乘法累数制:中国数字
4600不必写成“千千千千百百百百百百”
4.代数问题和几何问题
1、书中有几个问题属于现代代数的一元一次方程问题:一个量,加上自身的七分之一等于19.现代解法很简单,但是纸草书中解法很难,但是答案却是正确的。
2、给出了一些求面积和体积的题,得到的结果不够精确。尽管埃及是几何学的发源地,但是几何水平不高。
3.几何学的诞生
尼罗河是埃及的母亲河,拉绳者面积测量
数学科学最早在埃及兴起,因为那里的祭司才有足够的闲暇
实验阶段,几何知识是零碎的,片段的,直到希腊人占领这儿。
二、古巴比伦的数学
早在公元前四五千年,两河流域的苏美尔人用削尖的芦苇杆在泥板上写字,晒干后泥板书,字形像楔子,叫做楔形字。
1、楔形文字中的记数法
记数方法:10进制和60进制混用
简单累数制
2.泥板上的代数
代数和算术的区别(未知数、符号、方程)
现藏在耶鲁大学的泥板上:两个数的积为60,差为7(求根公式)
巴比伦人会求解指数方程
例:有一笔钱,年利率为20%,多长时间本金和利息一样多
3.泥板上的几何
古印度也有记载,在《测绳的法规》中提到
3.泥板上的几何
纽约哥伦比亚大学的真本图书馆内有一块公元前1900—_公元前1600的泥板,称为普林顿322号数学泥板
THANKS
同课章节目录
- 第一讲 早期的算术与几何
- 一 古埃及的数学
- 二 两河流域的数学
- 三 丰富多彩的记数制度
- 第二讲 古希腊数学
- 一 希腊数学的先行者
- 二 毕达哥拉斯学派
- 三 欧几里得与《原本》
- 四 数学之神──阿基米德
- 第三讲 中国古代数学瑰宝
- 一 《周髀算经》与赵爽弦图
- 二 《九章算术》
- 三 大衍求一术
- 四 中国古代数学家
- 第四讲 平面解析几何的产生
- 一 坐标思想的早期萌芽
- 二 笛卡儿坐标系
- 三 费马的解析几何思想
- 四 解析几何的进一步发展
- 第五讲 微积分的诞生
- 一 微积分产生的历史背景
- 二 科学巨人牛顿的工作
- 三 莱布尼茨的“微积分”
- 第六讲 近代数学两巨星
- 一 分析的化身──欧拉
- 二 数学王子──高斯
- 第七讲 千古谜题
- 一 三次、四次方程求根公式的发现
- 二 高次方程可解性问题的解决
- 三 伽罗瓦与群论
- 四 古希腊三大几何问题的解决
- 第八讲 对无穷的深入思考
- 一 古代的无穷观念
- 二 无穷集合论的创立
- 三 集合论的进一步发展与完善
- 第九讲 中国现代数学的开拓与发展
- 一 中国现代数学发展概观
- 二 人民的数学家──华罗庚
- 三 当代几何大师──陈省身
