高中数学人教新课标A版选修4-1第二讲 直线与圆的位置关系三 圆的切线的性质及判定定理 课件 28张PPT
文档属性
| 名称 | 高中数学人教新课标A版选修4-1第二讲 直线与圆的位置关系三 圆的切线的性质及判定定理 课件 28张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 769.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-25 13:04:07 | ||
图片预览



文档简介
(共28张PPT)
圆的切线的性质与判定
高中数学 选修4-1
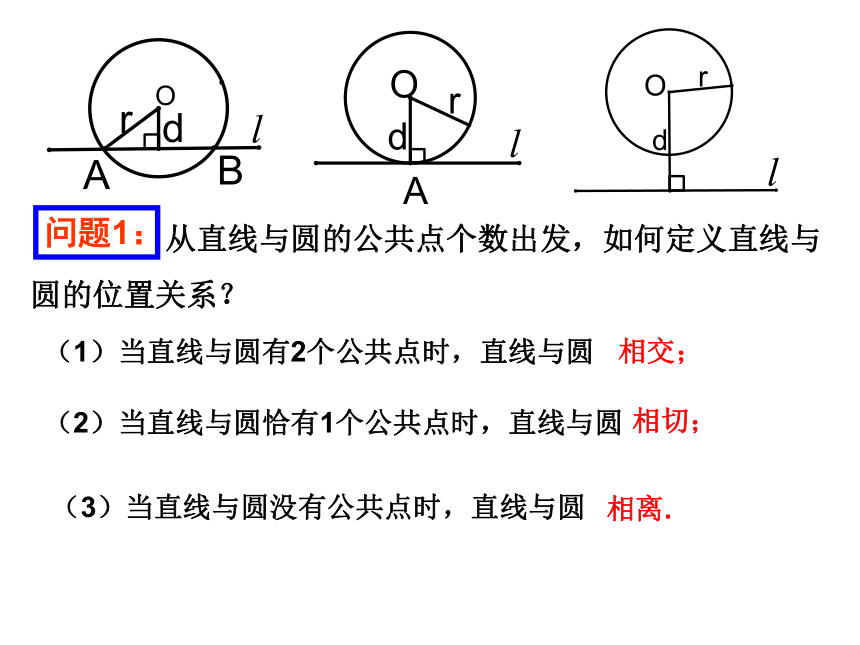
(1)当直线与圆有2个公共点时,直线与圆
相交;
(2)当直线与圆恰有1个公共点时,直线与圆
相切;
(3)当直线与圆没有公共点时,直线与圆
相离.
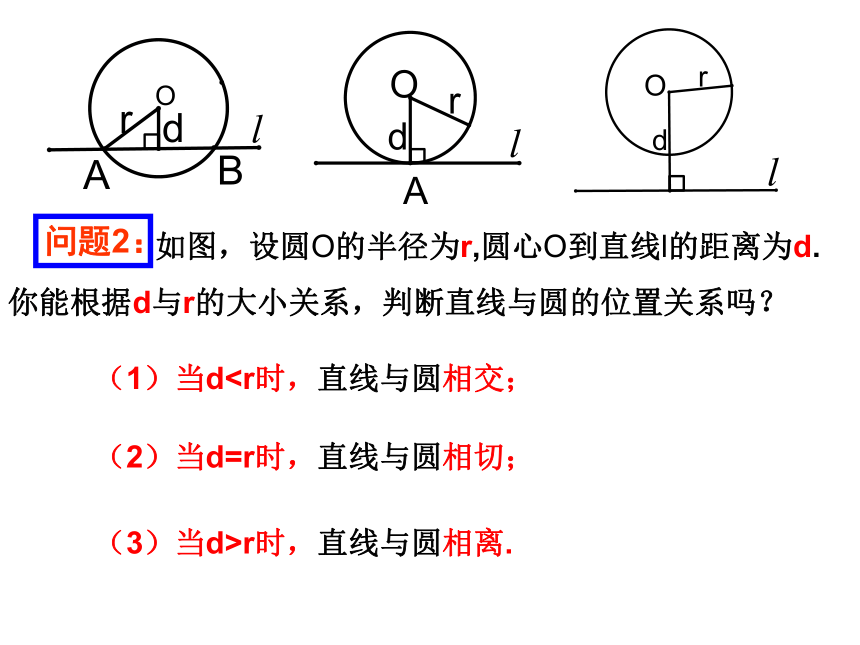
(1)当d(2)当d=r时,直线与圆相切;
(3)当d>r时,直线与圆相离.
(1)过圆O内一点A任意作一条直线l,那么直线l与圆O是什么位置关系?
(2)过圆O上一点A任意作一条直线l,那么直线l与圆O是什么位置关系?
问题3:
(3)过圆O上一点A如何作一条直线l,使得直线l与圆O相切呢?
相交
相交或相切
证明:在直线l上任取一点P,若点P不同于点A,则OP>OA,从而点P在圆O外.
故直线l与圆O只有一个公共点A.即l是圆O的切线.
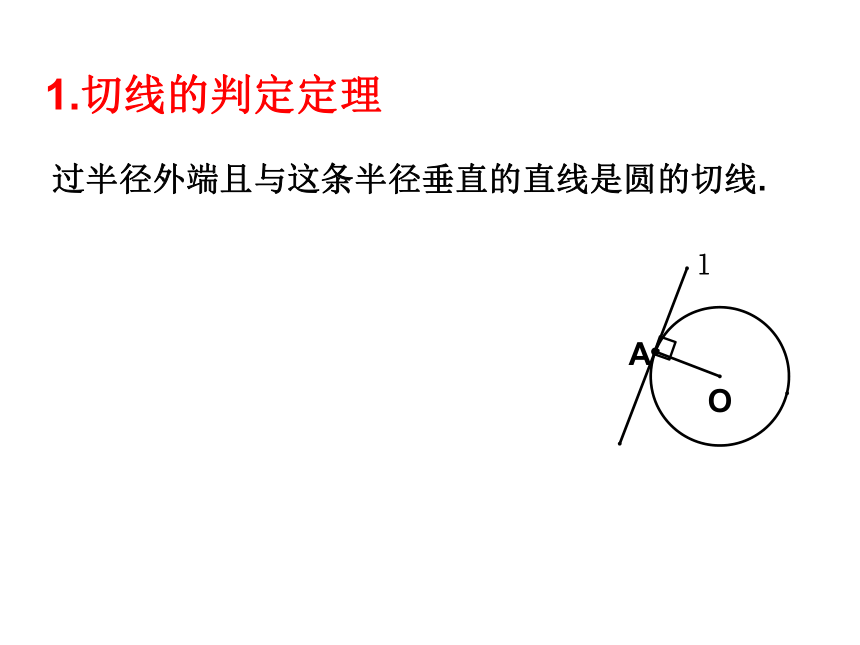
1.切线的判定定理
过半径外端且与这条半径垂直的直线是圆的切线.
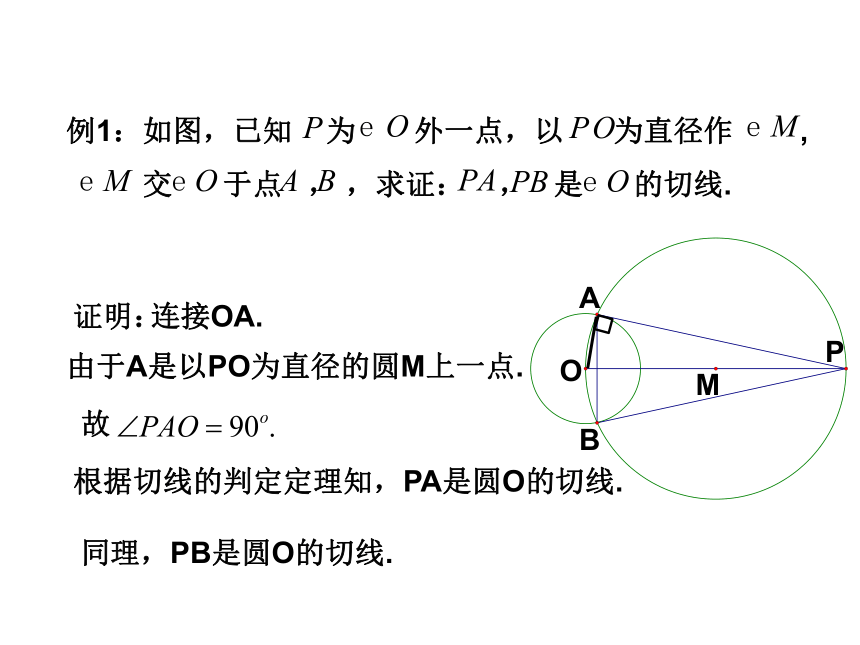
证明:
连接OA.
由于A是以PO为直径的圆M上一点.
根据切线的判定定理知,PA是圆O的切线.
同理,PB是圆O的切线.
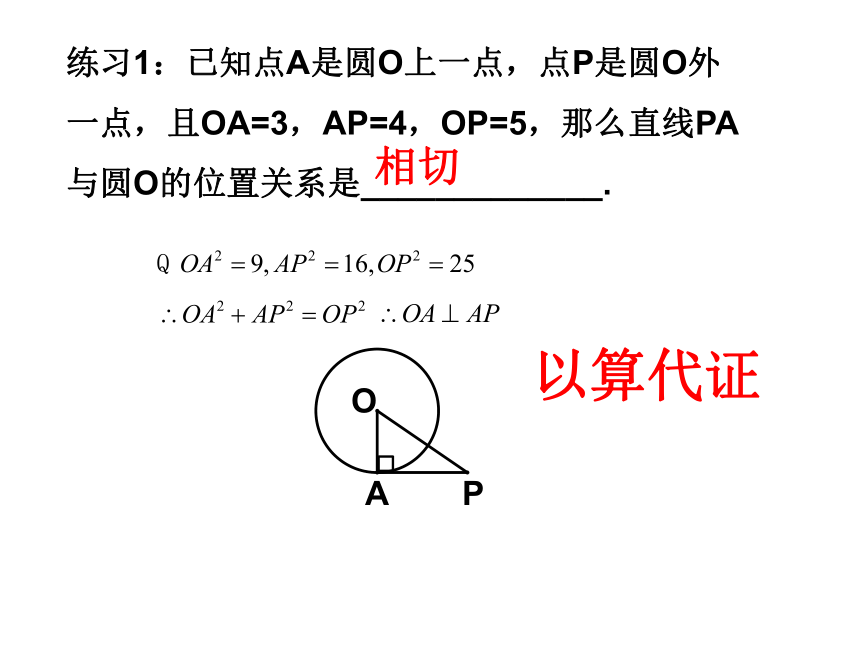
练习1:已知点A是圆O上一点,点P是圆O外一点,且OA=3,AP=4,OP=5,那么直线PA与圆O的位置关系是_____________.
相切
以算代证
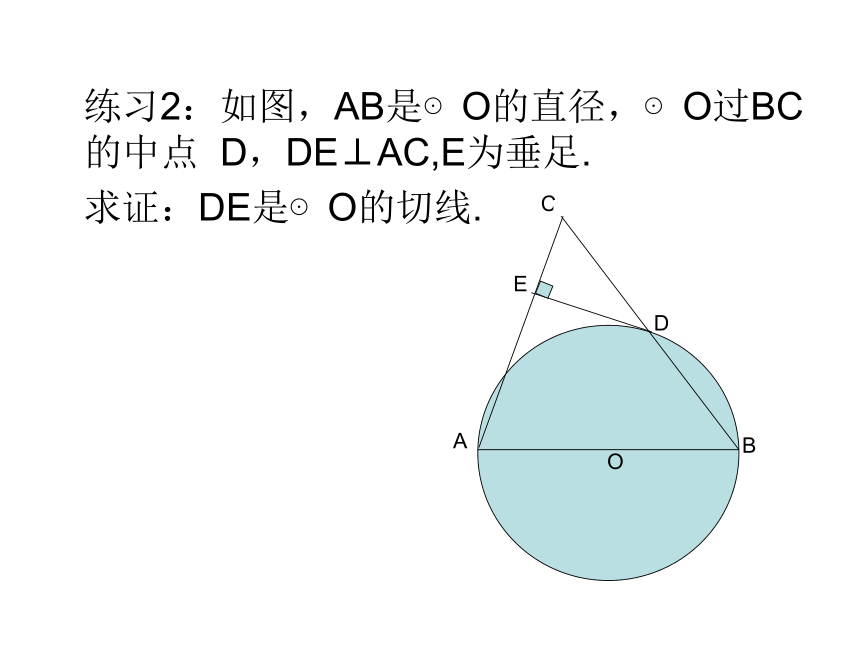
练习2:如图,AB是⊙O的直径,⊙O过BC的中点 D,DE⊥AC,E为垂足.
求证:DE是⊙O的切线.
P
证明:
反证法!
反证法一般步骤是什么?
1.反设
2.归谬
3.存真
2.切线的性质定理:
圆的切线垂直于经过切点的半径.
依据是切线的性质定理
为什么?
经过圆心且与切线垂直的直线必经过切点.
经过切点且与切线垂直的直线必经过圆心.
推论1:
为什么?
推论2:
例2: 如图,AB为⊙O的直径,C为⊙O上一点.AD和过C点的切线互相垂直,垂足为D.求证:AC平分∠DAB.
练习1:如图,OA和OB是⊙O的半径,并且OA⊥OB,P是OA上任意一点,BP的延长线交⊙O于Q.过Q作⊙O的切线交OA的延长线于R.
求证:RP=RQ.
例3:从圆外一点P引圆O的两条切线PA,PB,点A,B 为切点,求证:
(2)PO垂直平分线段AB.
证明:
(1)连接OA,OB,则
例3:从圆外一点P引圆O的两条切线PA,PB,点A,B 为切点,求证:
(2)PO垂直平分线段AB.
证明:
由等腰三角形三线合一定理知,
从圆外一点向圆作切线,该点到切点间线段的长称为切线长.
3.切线长的概念.
4.切线长定理.
从圆外一点引圆的两条切线,切线长相等.
Q
证明:
所以,以AB为直径的圆经过点P.故
由切线长定理知:
同理,
练习:如图,已知直角三角形的三条边长分别是3,4,5,求其内切圆半径r的值.
推广:已知直角三角形的三条边长分别是a,b,c,(c为斜边长)求其内切圆半径r的值(结果用a,b,c)表示.
从特殊到一般
1.如图,△ABC为等腰三角形,O是底边BC的中点,⊙O与腰AB相切于 点D.求证:AC与⊙O相切.
巩固训练
2.如图,AB是⊙O的直径,直线BC是⊙O的切线,切点为B,且OC∥AD,AD是弦.求证:DC是⊙O的切线.
3.把两圆的外公切线夹在两切点间的线段的长称为两圆外公切线的长,求证:外切圆的外公切线的长等于内公切线夹在外公切线间的线段长.
4.如图,P是半圆O的直径BC的延长线上一点,PA切半圆于点A, 于点H.若PA=1,PB+PC=a(a>2),求PH的长.
5.求证:相离两圆的内公切线夹在外公切线间的线段长等于两圆外公切线的长.
6.如图,AB是圆O的直径,C是圆O上的一点,过点C的切线与过A,B两点的切线分别交于点E,F,连接AF与BE交于点P,求证:
本节课小结
1.切线的判定定理
过半径外端且与这条半径垂直的直线是圆的切线.
2.切线的性质定理:
圆的切线垂直于经过切点的半径.
经过圆心且与切线垂直的直线必经过切点.
经过切点且与切线垂直的直线必经过圆心.
推论1:
推论2:
3.切线长定理.
从圆外一点引圆的两条切线,切线长相等.
一.本节课我们学习了哪些定理?
二.几何证明的一般原则是什么?
有理有据
三.本节课我们学习哪些数学思想与方法?
圆的切线的性质与判定
高中数学 选修4-1
(1)当直线与圆有2个公共点时,直线与圆
相交;
(2)当直线与圆恰有1个公共点时,直线与圆
相切;
(3)当直线与圆没有公共点时,直线与圆
相离.
(1)当d
(3)当d>r时,直线与圆相离.
(1)过圆O内一点A任意作一条直线l,那么直线l与圆O是什么位置关系?
(2)过圆O上一点A任意作一条直线l,那么直线l与圆O是什么位置关系?
问题3:
(3)过圆O上一点A如何作一条直线l,使得直线l与圆O相切呢?
相交
相交或相切
证明:在直线l上任取一点P,若点P不同于点A,则OP>OA,从而点P在圆O外.
故直线l与圆O只有一个公共点A.即l是圆O的切线.
1.切线的判定定理
过半径外端且与这条半径垂直的直线是圆的切线.
证明:
连接OA.
由于A是以PO为直径的圆M上一点.
根据切线的判定定理知,PA是圆O的切线.
同理,PB是圆O的切线.
练习1:已知点A是圆O上一点,点P是圆O外一点,且OA=3,AP=4,OP=5,那么直线PA与圆O的位置关系是_____________.
相切
以算代证
练习2:如图,AB是⊙O的直径,⊙O过BC的中点 D,DE⊥AC,E为垂足.
求证:DE是⊙O的切线.
P
证明:
反证法!
反证法一般步骤是什么?
1.反设
2.归谬
3.存真
2.切线的性质定理:
圆的切线垂直于经过切点的半径.
依据是切线的性质定理
为什么?
经过圆心且与切线垂直的直线必经过切点.
经过切点且与切线垂直的直线必经过圆心.
推论1:
为什么?
推论2:
例2: 如图,AB为⊙O的直径,C为⊙O上一点.AD和过C点的切线互相垂直,垂足为D.求证:AC平分∠DAB.
练习1:如图,OA和OB是⊙O的半径,并且OA⊥OB,P是OA上任意一点,BP的延长线交⊙O于Q.过Q作⊙O的切线交OA的延长线于R.
求证:RP=RQ.
例3:从圆外一点P引圆O的两条切线PA,PB,点A,B 为切点,求证:
(2)PO垂直平分线段AB.
证明:
(1)连接OA,OB,则
例3:从圆外一点P引圆O的两条切线PA,PB,点A,B 为切点,求证:
(2)PO垂直平分线段AB.
证明:
由等腰三角形三线合一定理知,
从圆外一点向圆作切线,该点到切点间线段的长称为切线长.
3.切线长的概念.
4.切线长定理.
从圆外一点引圆的两条切线,切线长相等.
Q
证明:
所以,以AB为直径的圆经过点P.故
由切线长定理知:
同理,
练习:如图,已知直角三角形的三条边长分别是3,4,5,求其内切圆半径r的值.
推广:已知直角三角形的三条边长分别是a,b,c,(c为斜边长)求其内切圆半径r的值(结果用a,b,c)表示.
从特殊到一般
1.如图,△ABC为等腰三角形,O是底边BC的中点,⊙O与腰AB相切于 点D.求证:AC与⊙O相切.
巩固训练
2.如图,AB是⊙O的直径,直线BC是⊙O的切线,切点为B,且OC∥AD,AD是弦.求证:DC是⊙O的切线.
3.把两圆的外公切线夹在两切点间的线段的长称为两圆外公切线的长,求证:外切圆的外公切线的长等于内公切线夹在外公切线间的线段长.
4.如图,P是半圆O的直径BC的延长线上一点,PA切半圆于点A, 于点H.若PA=1,PB+PC=a(a>2),求PH的长.
5.求证:相离两圆的内公切线夹在外公切线间的线段长等于两圆外公切线的长.
6.如图,AB是圆O的直径,C是圆O上的一点,过点C的切线与过A,B两点的切线分别交于点E,F,连接AF与BE交于点P,求证:
本节课小结
1.切线的判定定理
过半径外端且与这条半径垂直的直线是圆的切线.
2.切线的性质定理:
圆的切线垂直于经过切点的半径.
经过圆心且与切线垂直的直线必经过切点.
经过切点且与切线垂直的直线必经过圆心.
推论1:
推论2:
3.切线长定理.
从圆外一点引圆的两条切线,切线长相等.
一.本节课我们学习了哪些定理?
二.几何证明的一般原则是什么?
有理有据
三.本节课我们学习哪些数学思想与方法?
