高中数学人教新课标A版选修4-4第一章 坐标系1.1.6 柱坐标系与球坐标系 课件 24张PPT
文档属性
| 名称 | 高中数学人教新课标A版选修4-4第一章 坐标系1.1.6 柱坐标系与球坐标系 课件 24张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 718.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-25 00:00:00 | ||
图片预览






文档简介
(共24张PPT)
第一章 坐标系
1.1.6 柱坐标系与球坐标系
数学选修4-4:坐标系与参数方程
Q
(x,y)
x
y
o
z
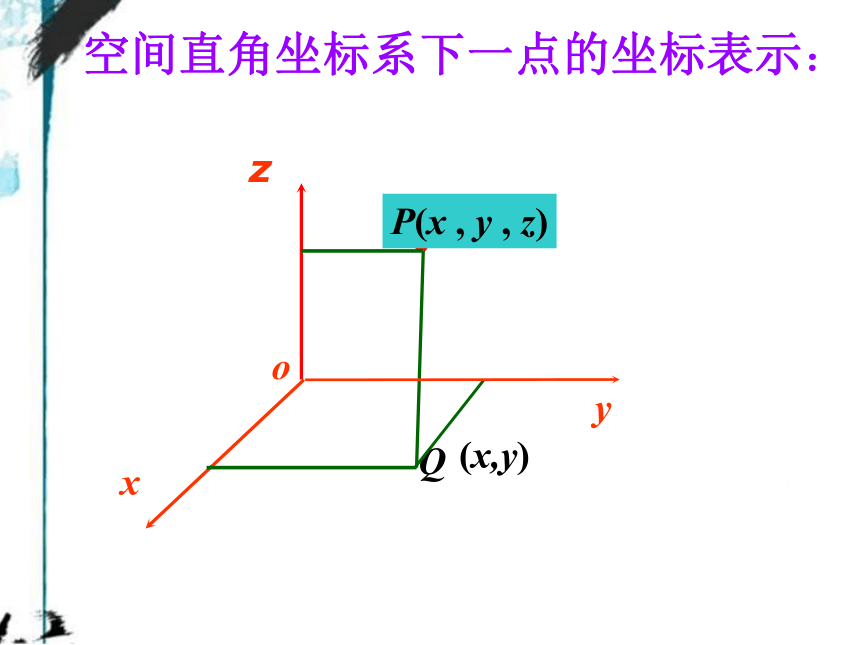
空间直角坐标系下一点的坐标表示:
P(x , y , z)
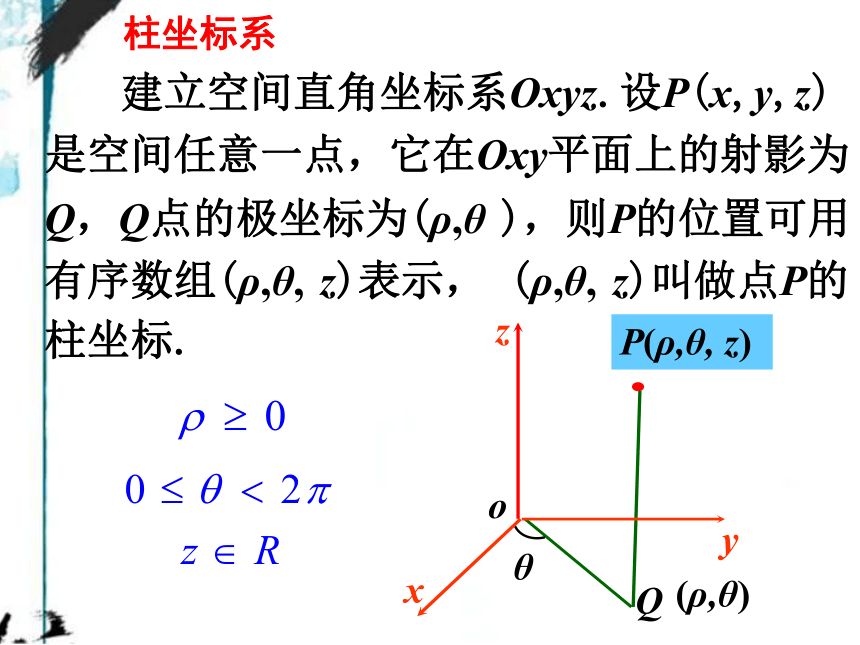
柱坐标系
建立空间直角坐标系Oxyz.设P(x,y,z)是空间任意一点,它在Oxy平面上的射影为Q,Q点的极坐标为(ρ,θ ),则P的位置可用有序数组(ρ,θ, z)表示, (ρ,θ, z)叫做点P的柱坐标.
Q
θ
P(x , y , z)
P(ρ,θ, z)
(ρ,θ)
x
y
z
o
柱坐标与空间直角坐标的互化
(1)柱坐标转化为直角坐标
(2)直角坐标转化为柱坐标
柱坐标与空间直角坐标的互化
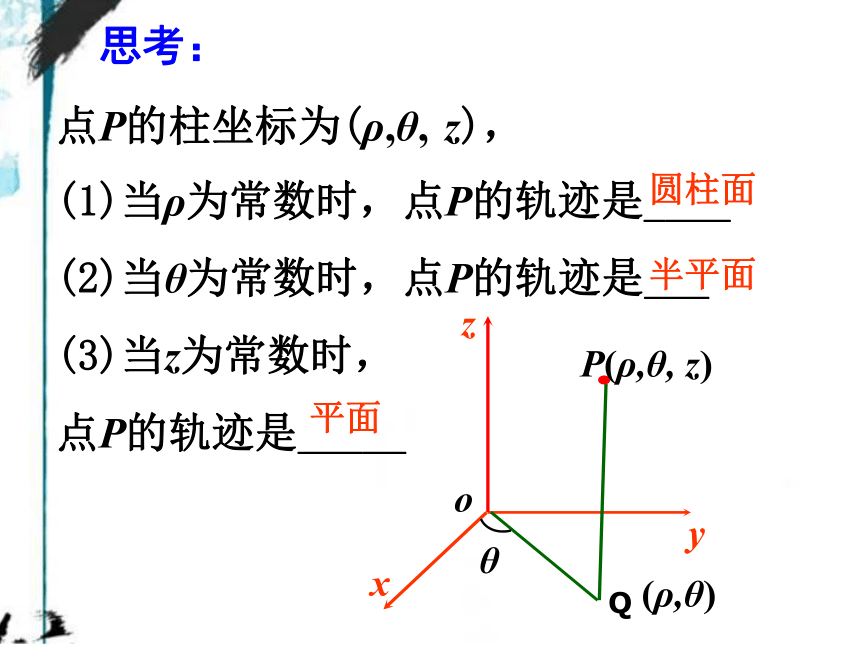
思考:
点P的柱坐标为(ρ,θ, z),
(1)当ρ为常数时,点P的轨迹是____
(2)当θ为常数时,点P的轨迹是___
(3)当z为常数时,
点P的轨迹是_____
圆柱面
半平面
平面
θ
x
y
z
o
P(ρ,θ, z)
(ρ,θ)
Q
例题分析1 (1)若点P的柱坐标为 ,则它的直角坐标为 ;?
(2)已知点M的直角坐标为(0,1,5),则它的柱坐标为 .?
θ
x
y
z
o
Q
P(r, j ,θ)
P
r
P(r, j ,θ)
球坐标系
球坐标系
建立空间直角坐标系Oxyz.设P(x,y,z)是空间任意一点,记|OP|=r,OP与Oz轴正向所夹的角为j.点P在Oxy平面上的射影为Q,Ox轴按逆时针方向旋转到OQ时所转过的最小正角为θ.则P的位置可用有序数组(r, j ,θ)表示, (r, j ,θ)叫做点P的球坐标.
θ
x
y
z
o
Q
P(r, j ,θ)
P
r
P(r, j ,θ)
球坐标系
球坐标转化为直角坐标:
x
θ
y
o
Q
P(r, j ,θ)
r
z
直角坐标转化为球坐标:
x
θ
y
o
Q
P(r, j ,θ)
r
z
注意由角所在象限确定角。
B基础训练达标
思考:
点P的球坐标为(r, j ,θ) ,
(1)当r为常数时,点P的轨迹是____
(2)当 j为常数时,点P的轨迹是____
(3)当θ为常数时,
点P的轨迹是___
球面
圆锥面或平面
半平面
θ
x
y
z
o
Q
P(r, j , θ)
r
小结作业
1.柱坐标系是由平面极坐标系和空间直角坐标系中的一部分建立起来的,所以柱坐标系又叫半极坐标系,其中柱坐标(ρ,θ,z)的前两个坐标分量就是平面极坐标,后一个坐标分量就是空间直角坐标系中的竖坐标.
2.球坐标系在地理学、天文学中有着广泛的应用,在测量实践中,角θ称为被测点P(r,φ,θ)的方位角,90°-φ称为高低角.
3.坐标系是联系数与形的桥梁,利用坐标系可以实现几何问题与代数问题的相互转化.但不同的坐标系有不同的特点,在实际应用时,要根据问题的特点选择适当的坐标系,使研究过程方便、简捷.
提高训练
设地球的半径为R,在球坐标系中,点A的坐标为(R,45°,70°),点B的坐标为(R,45°,160°),求A,B两点间的球面距离.
第一章 坐标系
1.1.6 柱坐标系与球坐标系
数学选修4-4:坐标系与参数方程
Q
(x,y)
x
y
o
z
空间直角坐标系下一点的坐标表示:
P(x , y , z)
柱坐标系
建立空间直角坐标系Oxyz.设P(x,y,z)是空间任意一点,它在Oxy平面上的射影为Q,Q点的极坐标为(ρ,θ ),则P的位置可用有序数组(ρ,θ, z)表示, (ρ,θ, z)叫做点P的柱坐标.
Q
θ
P(x , y , z)
P(ρ,θ, z)
(ρ,θ)
x
y
z
o
柱坐标与空间直角坐标的互化
(1)柱坐标转化为直角坐标
(2)直角坐标转化为柱坐标
柱坐标与空间直角坐标的互化
思考:
点P的柱坐标为(ρ,θ, z),
(1)当ρ为常数时,点P的轨迹是____
(2)当θ为常数时,点P的轨迹是___
(3)当z为常数时,
点P的轨迹是_____
圆柱面
半平面
平面
θ
x
y
z
o
P(ρ,θ, z)
(ρ,θ)
Q
例题分析1 (1)若点P的柱坐标为 ,则它的直角坐标为 ;?
(2)已知点M的直角坐标为(0,1,5),则它的柱坐标为 .?
θ
x
y
z
o
Q
P(r, j ,θ)
P
r
P(r, j ,θ)
球坐标系
球坐标系
建立空间直角坐标系Oxyz.设P(x,y,z)是空间任意一点,记|OP|=r,OP与Oz轴正向所夹的角为j.点P在Oxy平面上的射影为Q,Ox轴按逆时针方向旋转到OQ时所转过的最小正角为θ.则P的位置可用有序数组(r, j ,θ)表示, (r, j ,θ)叫做点P的球坐标.
θ
x
y
z
o
Q
P(r, j ,θ)
P
r
P(r, j ,θ)
球坐标系
球坐标转化为直角坐标:
x
θ
y
o
Q
P(r, j ,θ)
r
z
直角坐标转化为球坐标:
x
θ
y
o
Q
P(r, j ,θ)
r
z
注意由角所在象限确定角。
B基础训练达标
思考:
点P的球坐标为(r, j ,θ) ,
(1)当r为常数时,点P的轨迹是____
(2)当 j为常数时,点P的轨迹是____
(3)当θ为常数时,
点P的轨迹是___
球面
圆锥面或平面
半平面
θ
x
y
z
o
Q
P(r, j , θ)
r
小结作业
1.柱坐标系是由平面极坐标系和空间直角坐标系中的一部分建立起来的,所以柱坐标系又叫半极坐标系,其中柱坐标(ρ,θ,z)的前两个坐标分量就是平面极坐标,后一个坐标分量就是空间直角坐标系中的竖坐标.
2.球坐标系在地理学、天文学中有着广泛的应用,在测量实践中,角θ称为被测点P(r,φ,θ)的方位角,90°-φ称为高低角.
3.坐标系是联系数与形的桥梁,利用坐标系可以实现几何问题与代数问题的相互转化.但不同的坐标系有不同的特点,在实际应用时,要根据问题的特点选择适当的坐标系,使研究过程方便、简捷.
提高训练
设地球的半径为R,在球坐标系中,点A的坐标为(R,45°,70°),点B的坐标为(R,45°,160°),求A,B两点间的球面距离.
