2020春华师大版九下数学27.4正多边形和圆同步课堂练习含答案
文档属性
| 名称 | 2020春华师大版九下数学27.4正多边形和圆同步课堂练习含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-21 16:06:38 | ||
图片预览




文档简介
2020春华师大版九下数学27.4正多边形和圆同步课堂练习(学生版)
基础题
知识点1 认识正多边形
1.下面图形中,是正多边形的是( )
A.矩形 B.菱形
C.正方形 D.等腰梯形
2.一个正多边形的内角和是外角和的2倍,那么它是( )
A.正六边形 B.正八边形
C.正十边形 D.正十二边形
3.下列图形中,既是轴对称图形,又是中心对称图形的有( )
①正三角形;②正方形;③正五边形;④正六边形;⑤线段;⑥圆;⑦菱形;⑧平行四边形.
A.3个 B.4个
C.5个 D.6个
4.如图,一束平行太阳光线照射到正五边形上,则∠1= .
知识点2 与正多边形有关的计算
5.正多边形的中心角是30°,那么这个正多边形的边数是( )
A.12 B.10
C.8 D.6
6.已知圆内接正三角形的边心距为1,则这个三角形的面积为( )
A.2 B.3
C.4 D.6
7.如图,正六边形ABCDEF内接于⊙O,连结BD,则∠CBD的度数是( )
A.30° B.45°
C.60° D.90°
8.若正方形的外接圆半径为2,则其内切圆半径为( )
A. B.2
C. D.1
9.已知正六边形ABCDEF的边心距为 cm,则正六边形的半径为 cm.
10.如图,四边形ABCD是⊙O的内接正方形,若正方形的面积等于4,则⊙O的面积等于 .
11.若一个正六边形的周长为24,求该正六边形的面积.(结果保留根号)
知识点3 等分圆画正多边形
12.高斯用直尺和圆规作出了正十七边形,如图,正十七边形的一边所对的外接圆的圆心角∠AOB的度数近似于( )
A.11° B.17° C.21° D.25°
13.尺规作图特有的魅力曾使无数人沉湎其中,连当年叱咤风云的拿破仑也不例外,我们可以只用圆规将圆等分.例如可将圆6等分,如图,只需在⊙O上任取点A,从点A开始,以⊙O的半径长为半径,在⊙O上依次截取点B,C,D,E,F.从而点A,B,C,D,E,F把⊙O六等分.下列可以只用圆规等分的是( )
①两等分;②三等分;③四等分;④五等分.
A.② B.①② C.①②③ D.①②③④
中档题
14.如图,在⊙O中,OA=AB,OC⊥AB交⊙O于点C,则下列结论错误的是( )
A.弦AB的长等于圆内接正六边形的边长
B.弦AC的长等于圆内接正十二边形的边长
C.=
D.∠BAC=30°
15.正多边形的内切圆与外接圆的周长之比为∶2,则这个正多边形为( )
A.正十二边形 B.正六边形
C.正四边形 D.正三角形
16.以半径为1的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则该三角形的面积是( )
A. B. C. D.
17.如图,五边形ABCDE是⊙O的内接正五边形,AF是⊙O的直径,则∠BDF的度数是 .
18.如图,AC是⊙O的内接正六边形的一边,点B在上,且BC是⊙O的内接正十边形的一边.若AB是⊙O的内接正n边形的一边,则n= .
19.画一个半径为2 cm的正五边形,再作出这个五边形各条对角线,画出一个五角星.
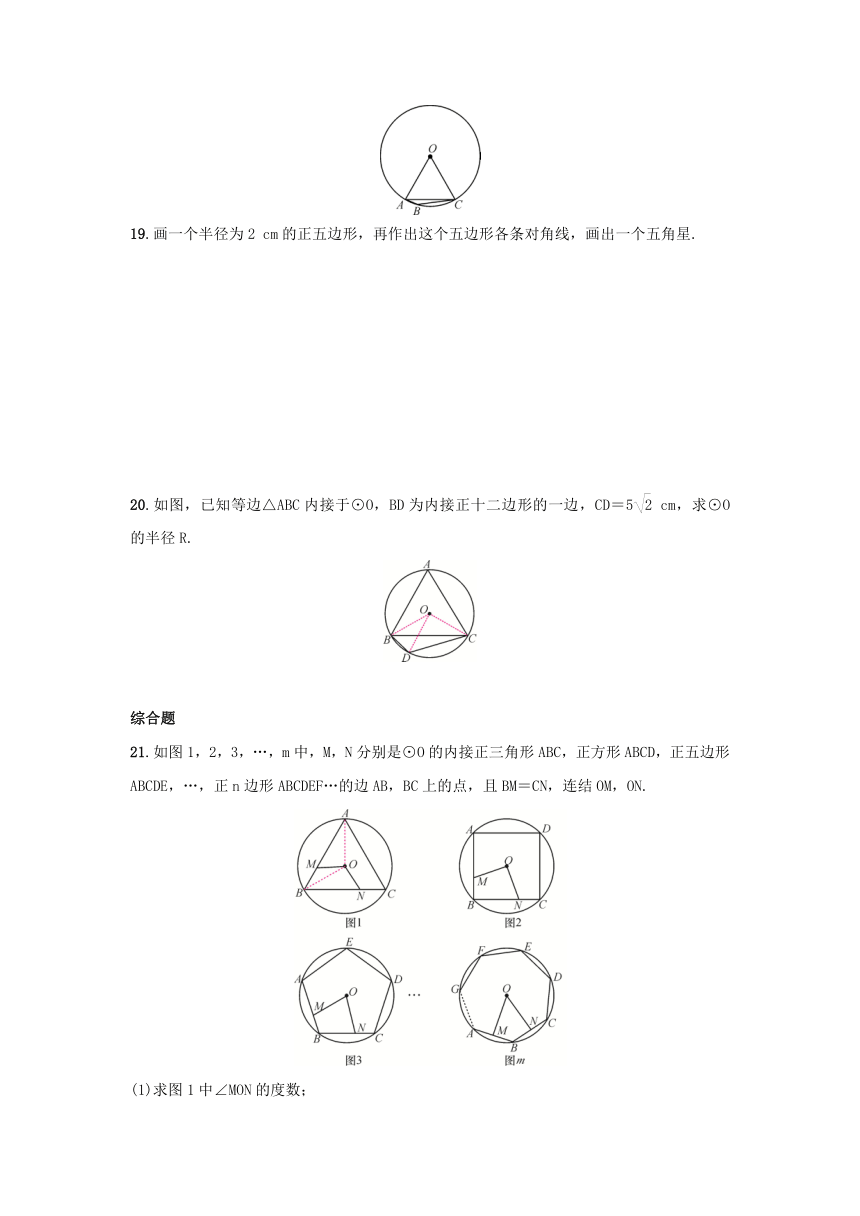
20.如图,已知等边△ABC内接于⊙O,BD为内接正十二边形的一边,CD=5 cm,求⊙O的半径R.
综合题
21.如图1,2,3,…,m中,M,N分别是⊙O的内接正三角形ABC,正方形ABCD,正五边形ABCDE,…,正n边形ABCDEF…的边AB,BC上的点,且BM=CN,连结OM,ON.
(1)求图1中∠MON的度数;
(2)图2中∠MON的度数是 ,图3中∠MON的度数是 ;
(3)试探究∠MON的度数与正n边形边数n的关系(直接写出答案).
2020春华师大版九下数学27.4正多边形和圆同步课堂练习(教师版)
基础题
知识点1 认识正多边形
1.下面图形中,是正多边形的是(C)
A.矩形 B.菱形
C.正方形 D.等腰梯形
2.一个正多边形的内角和是外角和的2倍,那么它是(A)
A.正六边形 B.正八边形
C.正十边形 D.正十二边形
3.下列图形中,既是轴对称图形,又是中心对称图形的有(C)
①正三角形;②正方形;③正五边形;④正六边形;⑤线段;⑥圆;⑦菱形;⑧平行四边形.
A.3个 B.4个
C.5个 D.6个
4.如图,一束平行太阳光线照射到正五边形上,则∠1=30°.
知识点2 与正多边形有关的计算
5.正多边形的中心角是30°,那么这个正多边形的边数是(A)
A.12 B.10
C.8 D.6
6.已知圆内接正三角形的边心距为1,则这个三角形的面积为(B)
A.2 B.3
C.4 D.6
7.如图,正六边形ABCDEF内接于⊙O,连结BD,则∠CBD的度数是(A)
A.30° B.45°
C.60° D.90°
8.若正方形的外接圆半径为2,则其内切圆半径为(A)
A. B.2
C. D.1
9.已知正六边形ABCDEF的边心距为 cm,则正六边形的半径为2cm.
10.如图,四边形ABCD是⊙O的内接正方形,若正方形的面积等于4,则⊙O的面积等于2π.
11.若一个正六边形的周长为24,求该正六边形的面积.(结果保留根号)
解:如图,过点O作OD⊥AB,垂足为D.
∵∠AOB=360°÷6=60°,OA=OB,
∴△AOB为等边三角形,且三条对角线把正六边形分成了六个全等的等边三角形.
∵正六边形的周长为24,∴AB=4.
∵OD⊥AB,∴∠AOD=30°,AD=2.
在Rt△AOD中,根据勾股定理,得OD=2.
∴S△AOB=×4×2=4.
∴S正六边形=6×4=24.
知识点3 等分圆画正多边形
12.高斯用直尺和圆规作出了正十七边形,如图,正十七边形的一边所对的外接圆的圆心角∠AOB的度数近似于(C)
A.11° B.17° C.21° D.25°
13.尺规作图特有的魅力曾使无数人沉湎其中,连当年叱咤风云的拿破仑也不例外,我们可以只用圆规将圆等分.例如可将圆6等分,如图,只需在⊙O上任取点A,从点A开始,以⊙O的半径长为半径,在⊙O上依次截取点B,C,D,E,F.从而点A,B,C,D,E,F把⊙O六等分.下列可以只用圆规等分的是(C)
①两等分;②三等分;③四等分;④五等分.
A.② B.①② C.①②③ D.①②③④
中档题
14.如图,在⊙O中,OA=AB,OC⊥AB交⊙O于点C,则下列结论错误的是(D)
A.弦AB的长等于圆内接正六边形的边长
B.弦AC的长等于圆内接正十二边形的边长
C.=
D.∠BAC=30°
15.正多边形的内切圆与外接圆的周长之比为∶2,则这个正多边形为(B)
A.正十二边形 B.正六边形
C.正四边形 D.正三角形
16.以半径为1的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则该三角形的面积是(D)
A. B. C. D.
17.如图,五边形ABCDE是⊙O的内接正五边形,AF是⊙O的直径,则∠BDF的度数是54°.
18.如图,AC是⊙O的内接正六边形的一边,点B在上,且BC是⊙O的内接正十边形的一边.若AB是⊙O的内接正n边形的一边,则n=15.
19.画一个半径为2 cm的正五边形,再作出这个五边形各条对角线,画出一个五角星.
解:画法:(1)以O为圆心,OA=2 cm为半径画圆;
(2)以O点为顶点,OA为一边作∠AOB=72°,再依次作∠BOC=∠COD=∠DOE=72°,分别与圆交于点B,C,D,E;
(3)分别连结AB,BC,CD,DE,EA.则正五边形ABCDE就是所要画的正五边形;
(4)依次连结AC,AD,BD,BE,CE.就画出了所要求的五角星.
20.如图,已知等边△ABC内接于⊙O,BD为内接正十二边形的一边,CD=5 cm,求⊙O的半径R.
解:连结OB,OC,OD,
∵等边△ABC内接于⊙O,BD为内接正十二边形的一边,
∴∠BOC=×360°=120°,∠BOD=×360°=30°.
∴∠COD=∠BOC-∠BOD=90°.
∵OC=OD,∴∠OCD=45°.
∴OC=CD·cos45°=5×=5(cm),
即⊙O的半径R=5 cm.
综合题
21.如图1,2,3,…,m中,M,N分别是⊙O的内接正三角形ABC,正方形ABCD,正五边形ABCDE,…,正n边形ABCDEF…的边AB,BC上的点,且BM=CN,连结OM,ON.
(1)求图1中∠MON的度数;
(2)图2中∠MON的度数是90°,图3中∠MON的度数是72°;
(3)试探究∠MON的度数与正n边形边数n的关系(直接写出答案).
解:(1)连结OA,OB.
∵正三角形ABC内接于⊙O,
∴AB=BC,∠OAM=∠OBN=30°,∠AOB=120°,OA=OB.
∵BM=CN,∴AM=BN.
∴△AOM≌△BON(SAS).
∴∠AOM=∠BON.
∴∠AOM+∠BOM=∠BON+∠BOM,
即∠AOB=∠MON=120°.
(3)∠MON=.
基础题
知识点1 认识正多边形
1.下面图形中,是正多边形的是( )
A.矩形 B.菱形
C.正方形 D.等腰梯形
2.一个正多边形的内角和是外角和的2倍,那么它是( )
A.正六边形 B.正八边形
C.正十边形 D.正十二边形
3.下列图形中,既是轴对称图形,又是中心对称图形的有( )
①正三角形;②正方形;③正五边形;④正六边形;⑤线段;⑥圆;⑦菱形;⑧平行四边形.
A.3个 B.4个
C.5个 D.6个
4.如图,一束平行太阳光线照射到正五边形上,则∠1= .
知识点2 与正多边形有关的计算
5.正多边形的中心角是30°,那么这个正多边形的边数是( )
A.12 B.10
C.8 D.6
6.已知圆内接正三角形的边心距为1,则这个三角形的面积为( )
A.2 B.3
C.4 D.6
7.如图,正六边形ABCDEF内接于⊙O,连结BD,则∠CBD的度数是( )
A.30° B.45°
C.60° D.90°
8.若正方形的外接圆半径为2,则其内切圆半径为( )
A. B.2
C. D.1
9.已知正六边形ABCDEF的边心距为 cm,则正六边形的半径为 cm.
10.如图,四边形ABCD是⊙O的内接正方形,若正方形的面积等于4,则⊙O的面积等于 .
11.若一个正六边形的周长为24,求该正六边形的面积.(结果保留根号)
知识点3 等分圆画正多边形
12.高斯用直尺和圆规作出了正十七边形,如图,正十七边形的一边所对的外接圆的圆心角∠AOB的度数近似于( )
A.11° B.17° C.21° D.25°
13.尺规作图特有的魅力曾使无数人沉湎其中,连当年叱咤风云的拿破仑也不例外,我们可以只用圆规将圆等分.例如可将圆6等分,如图,只需在⊙O上任取点A,从点A开始,以⊙O的半径长为半径,在⊙O上依次截取点B,C,D,E,F.从而点A,B,C,D,E,F把⊙O六等分.下列可以只用圆规等分的是( )
①两等分;②三等分;③四等分;④五等分.
A.② B.①② C.①②③ D.①②③④
中档题
14.如图,在⊙O中,OA=AB,OC⊥AB交⊙O于点C,则下列结论错误的是( )
A.弦AB的长等于圆内接正六边形的边长
B.弦AC的长等于圆内接正十二边形的边长
C.=
D.∠BAC=30°
15.正多边形的内切圆与外接圆的周长之比为∶2,则这个正多边形为( )
A.正十二边形 B.正六边形
C.正四边形 D.正三角形
16.以半径为1的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则该三角形的面积是( )
A. B. C. D.
17.如图,五边形ABCDE是⊙O的内接正五边形,AF是⊙O的直径,则∠BDF的度数是 .
18.如图,AC是⊙O的内接正六边形的一边,点B在上,且BC是⊙O的内接正十边形的一边.若AB是⊙O的内接正n边形的一边,则n= .
19.画一个半径为2 cm的正五边形,再作出这个五边形各条对角线,画出一个五角星.
20.如图,已知等边△ABC内接于⊙O,BD为内接正十二边形的一边,CD=5 cm,求⊙O的半径R.
综合题
21.如图1,2,3,…,m中,M,N分别是⊙O的内接正三角形ABC,正方形ABCD,正五边形ABCDE,…,正n边形ABCDEF…的边AB,BC上的点,且BM=CN,连结OM,ON.
(1)求图1中∠MON的度数;
(2)图2中∠MON的度数是 ,图3中∠MON的度数是 ;
(3)试探究∠MON的度数与正n边形边数n的关系(直接写出答案).
2020春华师大版九下数学27.4正多边形和圆同步课堂练习(教师版)
基础题
知识点1 认识正多边形
1.下面图形中,是正多边形的是(C)
A.矩形 B.菱形
C.正方形 D.等腰梯形
2.一个正多边形的内角和是外角和的2倍,那么它是(A)
A.正六边形 B.正八边形
C.正十边形 D.正十二边形
3.下列图形中,既是轴对称图形,又是中心对称图形的有(C)
①正三角形;②正方形;③正五边形;④正六边形;⑤线段;⑥圆;⑦菱形;⑧平行四边形.
A.3个 B.4个
C.5个 D.6个
4.如图,一束平行太阳光线照射到正五边形上,则∠1=30°.
知识点2 与正多边形有关的计算
5.正多边形的中心角是30°,那么这个正多边形的边数是(A)
A.12 B.10
C.8 D.6
6.已知圆内接正三角形的边心距为1,则这个三角形的面积为(B)
A.2 B.3
C.4 D.6
7.如图,正六边形ABCDEF内接于⊙O,连结BD,则∠CBD的度数是(A)
A.30° B.45°
C.60° D.90°
8.若正方形的外接圆半径为2,则其内切圆半径为(A)
A. B.2
C. D.1
9.已知正六边形ABCDEF的边心距为 cm,则正六边形的半径为2cm.
10.如图,四边形ABCD是⊙O的内接正方形,若正方形的面积等于4,则⊙O的面积等于2π.
11.若一个正六边形的周长为24,求该正六边形的面积.(结果保留根号)
解:如图,过点O作OD⊥AB,垂足为D.
∵∠AOB=360°÷6=60°,OA=OB,
∴△AOB为等边三角形,且三条对角线把正六边形分成了六个全等的等边三角形.
∵正六边形的周长为24,∴AB=4.
∵OD⊥AB,∴∠AOD=30°,AD=2.
在Rt△AOD中,根据勾股定理,得OD=2.
∴S△AOB=×4×2=4.
∴S正六边形=6×4=24.
知识点3 等分圆画正多边形
12.高斯用直尺和圆规作出了正十七边形,如图,正十七边形的一边所对的外接圆的圆心角∠AOB的度数近似于(C)
A.11° B.17° C.21° D.25°
13.尺规作图特有的魅力曾使无数人沉湎其中,连当年叱咤风云的拿破仑也不例外,我们可以只用圆规将圆等分.例如可将圆6等分,如图,只需在⊙O上任取点A,从点A开始,以⊙O的半径长为半径,在⊙O上依次截取点B,C,D,E,F.从而点A,B,C,D,E,F把⊙O六等分.下列可以只用圆规等分的是(C)
①两等分;②三等分;③四等分;④五等分.
A.② B.①② C.①②③ D.①②③④
中档题
14.如图,在⊙O中,OA=AB,OC⊥AB交⊙O于点C,则下列结论错误的是(D)
A.弦AB的长等于圆内接正六边形的边长
B.弦AC的长等于圆内接正十二边形的边长
C.=
D.∠BAC=30°
15.正多边形的内切圆与外接圆的周长之比为∶2,则这个正多边形为(B)
A.正十二边形 B.正六边形
C.正四边形 D.正三角形
16.以半径为1的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则该三角形的面积是(D)
A. B. C. D.
17.如图,五边形ABCDE是⊙O的内接正五边形,AF是⊙O的直径,则∠BDF的度数是54°.
18.如图,AC是⊙O的内接正六边形的一边,点B在上,且BC是⊙O的内接正十边形的一边.若AB是⊙O的内接正n边形的一边,则n=15.
19.画一个半径为2 cm的正五边形,再作出这个五边形各条对角线,画出一个五角星.
解:画法:(1)以O为圆心,OA=2 cm为半径画圆;
(2)以O点为顶点,OA为一边作∠AOB=72°,再依次作∠BOC=∠COD=∠DOE=72°,分别与圆交于点B,C,D,E;
(3)分别连结AB,BC,CD,DE,EA.则正五边形ABCDE就是所要画的正五边形;
(4)依次连结AC,AD,BD,BE,CE.就画出了所要求的五角星.
20.如图,已知等边△ABC内接于⊙O,BD为内接正十二边形的一边,CD=5 cm,求⊙O的半径R.
解:连结OB,OC,OD,
∵等边△ABC内接于⊙O,BD为内接正十二边形的一边,
∴∠BOC=×360°=120°,∠BOD=×360°=30°.
∴∠COD=∠BOC-∠BOD=90°.
∵OC=OD,∴∠OCD=45°.
∴OC=CD·cos45°=5×=5(cm),
即⊙O的半径R=5 cm.
综合题
21.如图1,2,3,…,m中,M,N分别是⊙O的内接正三角形ABC,正方形ABCD,正五边形ABCDE,…,正n边形ABCDEF…的边AB,BC上的点,且BM=CN,连结OM,ON.
(1)求图1中∠MON的度数;
(2)图2中∠MON的度数是90°,图3中∠MON的度数是72°;
(3)试探究∠MON的度数与正n边形边数n的关系(直接写出答案).
解:(1)连结OA,OB.
∵正三角形ABC内接于⊙O,
∴AB=BC,∠OAM=∠OBN=30°,∠AOB=120°,OA=OB.
∵BM=CN,∴AM=BN.
∴△AOM≌△BON(SAS).
∴∠AOM=∠BON.
∴∠AOM+∠BOM=∠BON+∠BOM,
即∠AOB=∠MON=120°.
(3)∠MON=.
