2020春华师大版九下数学27.3第2课时圆锥的侧面展开图同步课堂练习含答案
文档属性
| 名称 | 2020春华师大版九下数学27.3第2课时圆锥的侧面展开图同步课堂练习含答案 |
|
|
| 格式 | zip | ||
| 文件大小 | 344.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-21 00:00:00 | ||
图片预览



文档简介
2020春华师大版九下数学27.3第2课时圆锥的侧面展开图同步课堂练习(学生版)
基础题
知识点 圆锥的侧面展开图及相关计算
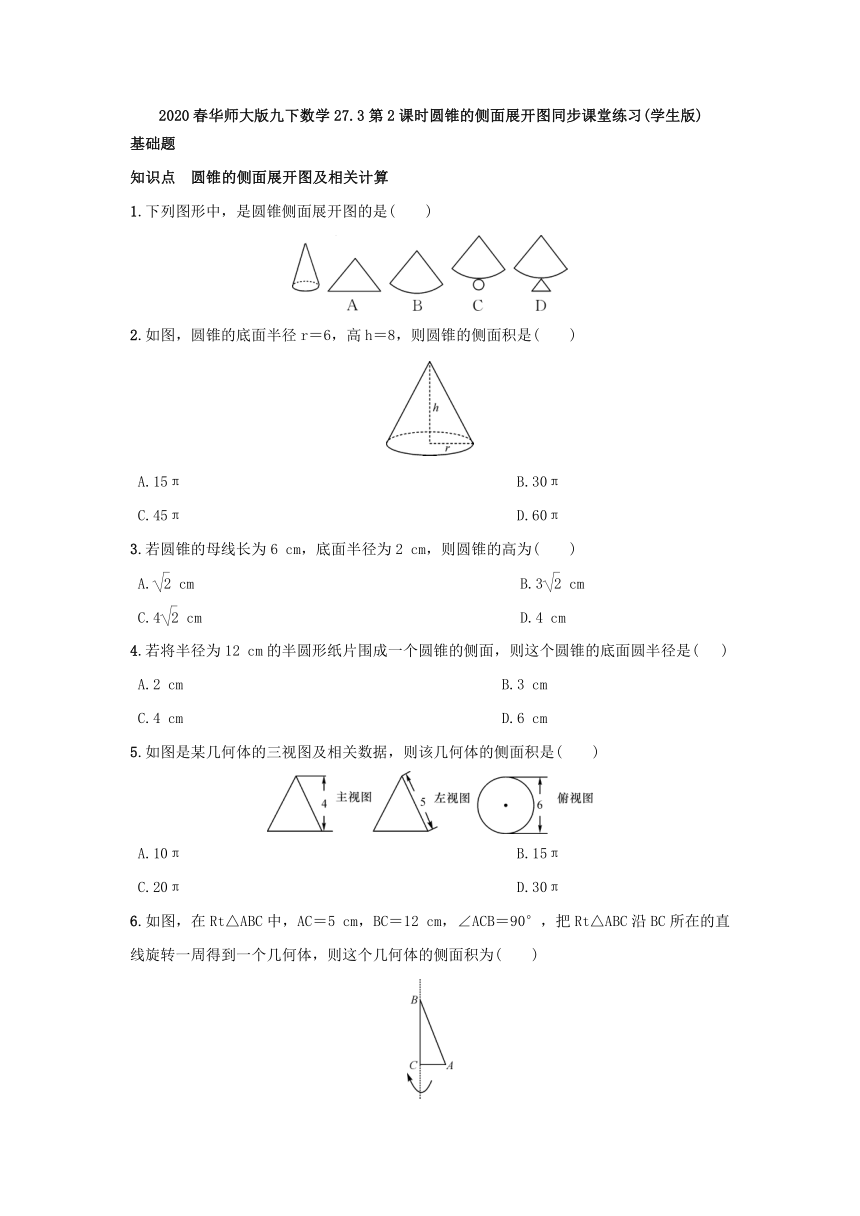
1.下列图形中,是圆锥侧面展开图的是( )
2.如图,圆锥的底面半径r=6,高h=8,则圆锥的侧面积是( )
A.15π B.30π
C.45π D.60π
3.若圆锥的母线长为6 cm,底面半径为2 cm,则圆锥的高为( )
A. cm B.3 cm
C.4 cm D.4 cm
4.若将半径为12 cm的半圆形纸片围成一个圆锥的侧面,则这个圆锥的底面圆半径是( )
A.2 cm B.3 cm
C.4 cm D.6 cm
5.如图是某几何体的三视图及相关数据,则该几何体的侧面积是( )
A.10π B.15π
C.20π D.30π
6.如图,在Rt△ABC中,AC=5 cm,BC=12 cm,∠ACB=90°,把Rt△ABC沿BC所在的直线旋转一周得到一个几何体,则这个几何体的侧面积为( )
A.60π cm2 B.65π cm2
C.120π cm2 D.130π cm2
7.若一个圆锥的底面圆的周长是5π cm,母线长是6 cm,则该圆锥的侧面展开图的圆心角度数是 .
8.一个圆锥的侧面展开图是半径为8 cm,圆心角为120°的扇形,则此圆锥的底面半径为 cm.
9.一个底面直径是80 cm,母线长为90 cm的圆锥的侧面展开图的圆心角的度数为 .
10.用一个圆心角为120°,半径为6的扇形做一个圆锥的侧面,则这个圆锥的底面圆的面积为 .
11.已知圆锥的侧面展开图是一个半径为12 cm,弧长为12π cm的扇形,求这个圆锥的侧面积及高.
中档题
12.如图,已知一块圆心角为270°的扇形铁皮,用它做一个圆锥形的烟囱帽(接缝忽略不计),圆锥底面圆的直径是60 cm,则这块扇形铁皮的半径是( )
A.40 cm B.50 cm
C.60 cm D.80 cm
13.将直径为60 cm的圆形铁皮,做成三个相同的圆锥容器的侧面(不浪费材料,不计接缝处的材料损耗),那么每个圆锥容器的底面半径为( )
A.10 cm B.30 cm
C.45 cm D.300 cm
14.如图,蒙古包可近似地看作由圆锥和圆柱组成.若用毛毡搭建一个底面圆面积为25π m2,圆柱高为3 m,圆锥高为2 m的蒙古包,则需要毛毡的面积是( )
A.(30+5)π m2 B.40π m2
C.(30+5)π m2 D.55π m2
15.如图所示,矩形纸片ABCD中,AD=6 cm,把它分割成正方形纸片ABFE和矩形纸片EFCD后,分别裁出扇形ABF和半径最大的圆,恰好能作为一个圆锥的侧面和底面,则AB的长为( )
A.3.5 cm B.4 cm
C.4.5 cm D.5 cm
16.若一圆锥的轴截面是等边三角形,则其侧面展开图的圆心角是 .
17.如图,一个圆锥形工艺品,它的高为3 cm,侧面展开图是半圆.求:
(1)圆锥的母线长与底面半径之比;
(2)圆锥的侧面积.
18.如图,有一直径是米的圆形铁皮,现从中剪出一个圆周角是90°的最大扇形ABC.
(1)求AB的长度;
(2)若用该扇形铁皮围成一个圆锥,则所得圆锥的底面圆的半径为多少米?
综合题
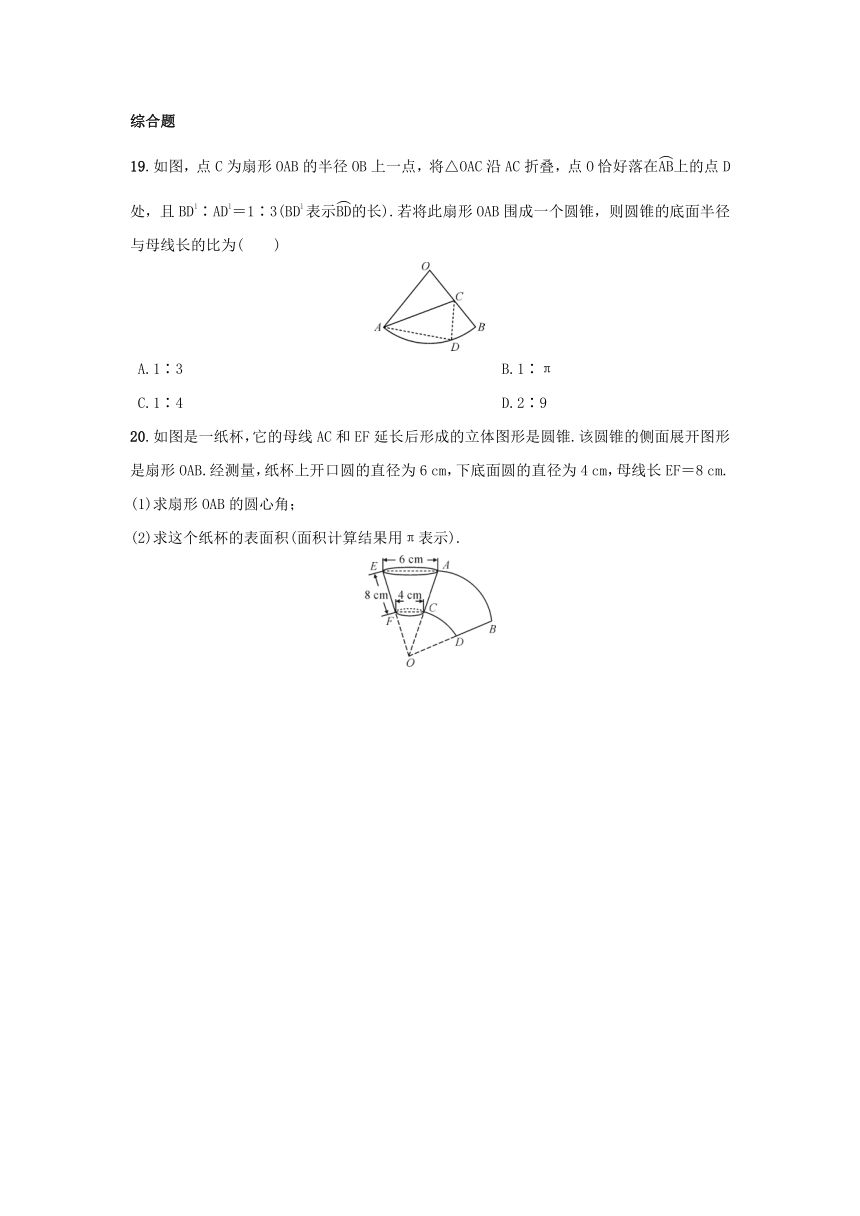
19.如图,点C为扇形OAB的半径OB上一点,将△OAC沿AC折叠,点O恰好落在上的点D处,且BDl∶ADl=1∶3(BDl表示的长).若将此扇形OAB围成一个圆锥,则圆锥的底面半径与母线长的比为( )
A.1∶3 B.1∶π
C.1∶4 D.2∶9
20.如图是一纸杯,它的母线AC和EF延长后形成的立体图形是圆锥.该圆锥的侧面展开图形是扇形OAB.经测量,纸杯上开口圆的直径为6 cm,下底面圆的直径为4 cm,母线长EF=8 cm.
(1)求扇形OAB的圆心角;
(2)求这个纸杯的表面积(面积计算结果用π表示).
2020春华师大版九下数学27.3第2课时圆锥的侧面展开图同步课堂练习(教师版)
基础题
知识点 圆锥的侧面展开图及相关计算
1.下列图形中,是圆锥侧面展开图的是(B)
2.如图,圆锥的底面半径r=6,高h=8,则圆锥的侧面积是(D)
A.15π B.30π
C.45π D.60π
3.若圆锥的母线长为6 cm,底面半径为2 cm,则圆锥的高为(C)
A. cm B.3 cm
C.4 cm D.4 cm
4.若将半径为12 cm的半圆形纸片围成一个圆锥的侧面,则这个圆锥的底面圆半径是(D)
A.2 cm B.3 cm
C.4 cm D.6 cm
5.如图是某几何体的三视图及相关数据,则该几何体的侧面积是(B)
A.10π B.15π
C.20π D.30π
6.如图,在Rt△ABC中,AC=5 cm,BC=12 cm,∠ACB=90°,把Rt△ABC沿BC所在的直线旋转一周得到一个几何体,则这个几何体的侧面积为(B)
A.60π cm2 B.65π cm2
C.120π cm2 D.130π cm2
7.若一个圆锥的底面圆的周长是5π cm,母线长是6 cm,则该圆锥的侧面展开图的圆心角度数是150°.
8.一个圆锥的侧面展开图是半径为8 cm,圆心角为120°的扇形,则此圆锥的底面半径为cm.
9.一个底面直径是80 cm,母线长为90 cm的圆锥的侧面展开图的圆心角的度数为160°.
10.用一个圆心角为120°,半径为6的扇形做一个圆锥的侧面,则这个圆锥的底面圆的面积为4π.
11.已知圆锥的侧面展开图是一个半径为12 cm,弧长为12π cm的扇形,求这个圆锥的侧面积及高.
解:这个圆锥的侧面积为×12×12π=72π(cm2),
设底面圆的半径为r cm,则2πr=12π,
解得r=6.
故这个圆锥的高为=6(cm).
中档题
12.如图,已知一块圆心角为270°的扇形铁皮,用它做一个圆锥形的烟囱帽(接缝忽略不计),圆锥底面圆的直径是60 cm,则这块扇形铁皮的半径是(A)
A.40 cm B.50 cm
C.60 cm D.80 cm
13.将直径为60 cm的圆形铁皮,做成三个相同的圆锥容器的侧面(不浪费材料,不计接缝处的材料损耗),那么每个圆锥容器的底面半径为(A)
A.10 cm B.30 cm
C.45 cm D.300 cm
14.如图,蒙古包可近似地看作由圆锥和圆柱组成.若用毛毡搭建一个底面圆面积为25π m2,圆柱高为3 m,圆锥高为2 m的蒙古包,则需要毛毡的面积是(A)
A.(30+5)π m2 B.40π m2
C.(30+5)π m2 D.55π m2
15.如图所示,矩形纸片ABCD中,AD=6 cm,把它分割成正方形纸片ABFE和矩形纸片EFCD后,分别裁出扇形ABF和半径最大的圆,恰好能作为一个圆锥的侧面和底面,则AB的长为(B)
A.3.5 cm B.4 cm
C.4.5 cm D.5 cm
16.若一圆锥的轴截面是等边三角形,则其侧面展开图的圆心角是180°.
17.如图,一个圆锥形工艺品,它的高为3 cm,侧面展开图是半圆.求:
(1)圆锥的母线长与底面半径之比;
(2)圆锥的侧面积.
解:(1)设圆锥底面半径为r cm,母线长为l cm,
由题意,知2πr=πl.
则l∶r=2∶1.
∴圆锥的母线长与底面半径之比为2∶1.
(2)由题意,知r2+(3)2=l2.
把l=2r代入,解得r1=-3(舍去),r2=3.
∴l=6.
∴圆锥的侧面积为πrl=18π cm2.
18.如图,有一直径是米的圆形铁皮,现从中剪出一个圆周角是90°的最大扇形ABC.
(1)求AB的长度;
(2)若用该扇形铁皮围成一个圆锥,则所得圆锥的底面圆的半径为多少米?
解:(1)∵∠BAC=90°,
∴BC为⊙O的直径,
即BC=米.
∴AB=BC=1米.
(2)设所得圆锥的底面圆的半径为r米,根据题意,得2πr=,解得r=.
∴底面圆的半径为米.
综合题
19.如图,点C为扇形OAB的半径OB上一点,将△OAC沿AC折叠,点O恰好落在上的点D处,且BDl∶ADl=1∶3(BDl表示的长).若将此扇形OAB围成一个圆锥,则圆锥的底面半径与母线长的比为(D)
A.1∶3 B.1∶π
C.1∶4 D.2∶9
20.如图是一纸杯,它的母线AC和EF延长后形成的立体图形是圆锥.该圆锥的侧面展开图形是扇形OAB.经测量,纸杯上开口圆的直径为6 cm,下底面圆的直径为4 cm,母线长EF=8 cm.
(1)求扇形OAB的圆心角;
(2)求这个纸杯的表面积(面积计算结果用π表示).
解:(1)由题意可知:
=6π cm,=4π cm.
设∠AOB=n°,AO=R cm,则CO=(R-8)cm,
由弧长公式得:=6π,=4π.
解方程组得
∴扇形OAB的圆心角是45°.
(2)∵R=24 cm,R-8=16 cm,
∴S扇形OCD=×4π×16=32π(cm2),
S扇形OAB=×6π×24=72π(cm2).
∴S纸杯侧面积=S扇形OAB-S扇形OCD=72π-32π=40π(cm2).
又∵S纸杯底面积=π×22=4π(cm2),
∴S纸杯表面积=40π+4π=44π(cm2).
基础题
知识点 圆锥的侧面展开图及相关计算
1.下列图形中,是圆锥侧面展开图的是( )
2.如图,圆锥的底面半径r=6,高h=8,则圆锥的侧面积是( )
A.15π B.30π
C.45π D.60π
3.若圆锥的母线长为6 cm,底面半径为2 cm,则圆锥的高为( )
A. cm B.3 cm
C.4 cm D.4 cm
4.若将半径为12 cm的半圆形纸片围成一个圆锥的侧面,则这个圆锥的底面圆半径是( )
A.2 cm B.3 cm
C.4 cm D.6 cm
5.如图是某几何体的三视图及相关数据,则该几何体的侧面积是( )
A.10π B.15π
C.20π D.30π
6.如图,在Rt△ABC中,AC=5 cm,BC=12 cm,∠ACB=90°,把Rt△ABC沿BC所在的直线旋转一周得到一个几何体,则这个几何体的侧面积为( )
A.60π cm2 B.65π cm2
C.120π cm2 D.130π cm2
7.若一个圆锥的底面圆的周长是5π cm,母线长是6 cm,则该圆锥的侧面展开图的圆心角度数是 .
8.一个圆锥的侧面展开图是半径为8 cm,圆心角为120°的扇形,则此圆锥的底面半径为 cm.
9.一个底面直径是80 cm,母线长为90 cm的圆锥的侧面展开图的圆心角的度数为 .
10.用一个圆心角为120°,半径为6的扇形做一个圆锥的侧面,则这个圆锥的底面圆的面积为 .
11.已知圆锥的侧面展开图是一个半径为12 cm,弧长为12π cm的扇形,求这个圆锥的侧面积及高.
中档题
12.如图,已知一块圆心角为270°的扇形铁皮,用它做一个圆锥形的烟囱帽(接缝忽略不计),圆锥底面圆的直径是60 cm,则这块扇形铁皮的半径是( )
A.40 cm B.50 cm
C.60 cm D.80 cm
13.将直径为60 cm的圆形铁皮,做成三个相同的圆锥容器的侧面(不浪费材料,不计接缝处的材料损耗),那么每个圆锥容器的底面半径为( )
A.10 cm B.30 cm
C.45 cm D.300 cm
14.如图,蒙古包可近似地看作由圆锥和圆柱组成.若用毛毡搭建一个底面圆面积为25π m2,圆柱高为3 m,圆锥高为2 m的蒙古包,则需要毛毡的面积是( )
A.(30+5)π m2 B.40π m2
C.(30+5)π m2 D.55π m2
15.如图所示,矩形纸片ABCD中,AD=6 cm,把它分割成正方形纸片ABFE和矩形纸片EFCD后,分别裁出扇形ABF和半径最大的圆,恰好能作为一个圆锥的侧面和底面,则AB的长为( )
A.3.5 cm B.4 cm
C.4.5 cm D.5 cm
16.若一圆锥的轴截面是等边三角形,则其侧面展开图的圆心角是 .
17.如图,一个圆锥形工艺品,它的高为3 cm,侧面展开图是半圆.求:
(1)圆锥的母线长与底面半径之比;
(2)圆锥的侧面积.
18.如图,有一直径是米的圆形铁皮,现从中剪出一个圆周角是90°的最大扇形ABC.
(1)求AB的长度;
(2)若用该扇形铁皮围成一个圆锥,则所得圆锥的底面圆的半径为多少米?
综合题
19.如图,点C为扇形OAB的半径OB上一点,将△OAC沿AC折叠,点O恰好落在上的点D处,且BDl∶ADl=1∶3(BDl表示的长).若将此扇形OAB围成一个圆锥,则圆锥的底面半径与母线长的比为( )
A.1∶3 B.1∶π
C.1∶4 D.2∶9
20.如图是一纸杯,它的母线AC和EF延长后形成的立体图形是圆锥.该圆锥的侧面展开图形是扇形OAB.经测量,纸杯上开口圆的直径为6 cm,下底面圆的直径为4 cm,母线长EF=8 cm.
(1)求扇形OAB的圆心角;
(2)求这个纸杯的表面积(面积计算结果用π表示).
2020春华师大版九下数学27.3第2课时圆锥的侧面展开图同步课堂练习(教师版)
基础题
知识点 圆锥的侧面展开图及相关计算
1.下列图形中,是圆锥侧面展开图的是(B)
2.如图,圆锥的底面半径r=6,高h=8,则圆锥的侧面积是(D)
A.15π B.30π
C.45π D.60π
3.若圆锥的母线长为6 cm,底面半径为2 cm,则圆锥的高为(C)
A. cm B.3 cm
C.4 cm D.4 cm
4.若将半径为12 cm的半圆形纸片围成一个圆锥的侧面,则这个圆锥的底面圆半径是(D)
A.2 cm B.3 cm
C.4 cm D.6 cm
5.如图是某几何体的三视图及相关数据,则该几何体的侧面积是(B)
A.10π B.15π
C.20π D.30π
6.如图,在Rt△ABC中,AC=5 cm,BC=12 cm,∠ACB=90°,把Rt△ABC沿BC所在的直线旋转一周得到一个几何体,则这个几何体的侧面积为(B)
A.60π cm2 B.65π cm2
C.120π cm2 D.130π cm2
7.若一个圆锥的底面圆的周长是5π cm,母线长是6 cm,则该圆锥的侧面展开图的圆心角度数是150°.
8.一个圆锥的侧面展开图是半径为8 cm,圆心角为120°的扇形,则此圆锥的底面半径为cm.
9.一个底面直径是80 cm,母线长为90 cm的圆锥的侧面展开图的圆心角的度数为160°.
10.用一个圆心角为120°,半径为6的扇形做一个圆锥的侧面,则这个圆锥的底面圆的面积为4π.
11.已知圆锥的侧面展开图是一个半径为12 cm,弧长为12π cm的扇形,求这个圆锥的侧面积及高.
解:这个圆锥的侧面积为×12×12π=72π(cm2),
设底面圆的半径为r cm,则2πr=12π,
解得r=6.
故这个圆锥的高为=6(cm).
中档题
12.如图,已知一块圆心角为270°的扇形铁皮,用它做一个圆锥形的烟囱帽(接缝忽略不计),圆锥底面圆的直径是60 cm,则这块扇形铁皮的半径是(A)
A.40 cm B.50 cm
C.60 cm D.80 cm
13.将直径为60 cm的圆形铁皮,做成三个相同的圆锥容器的侧面(不浪费材料,不计接缝处的材料损耗),那么每个圆锥容器的底面半径为(A)
A.10 cm B.30 cm
C.45 cm D.300 cm
14.如图,蒙古包可近似地看作由圆锥和圆柱组成.若用毛毡搭建一个底面圆面积为25π m2,圆柱高为3 m,圆锥高为2 m的蒙古包,则需要毛毡的面积是(A)
A.(30+5)π m2 B.40π m2
C.(30+5)π m2 D.55π m2
15.如图所示,矩形纸片ABCD中,AD=6 cm,把它分割成正方形纸片ABFE和矩形纸片EFCD后,分别裁出扇形ABF和半径最大的圆,恰好能作为一个圆锥的侧面和底面,则AB的长为(B)
A.3.5 cm B.4 cm
C.4.5 cm D.5 cm
16.若一圆锥的轴截面是等边三角形,则其侧面展开图的圆心角是180°.
17.如图,一个圆锥形工艺品,它的高为3 cm,侧面展开图是半圆.求:
(1)圆锥的母线长与底面半径之比;
(2)圆锥的侧面积.
解:(1)设圆锥底面半径为r cm,母线长为l cm,
由题意,知2πr=πl.
则l∶r=2∶1.
∴圆锥的母线长与底面半径之比为2∶1.
(2)由题意,知r2+(3)2=l2.
把l=2r代入,解得r1=-3(舍去),r2=3.
∴l=6.
∴圆锥的侧面积为πrl=18π cm2.
18.如图,有一直径是米的圆形铁皮,现从中剪出一个圆周角是90°的最大扇形ABC.
(1)求AB的长度;
(2)若用该扇形铁皮围成一个圆锥,则所得圆锥的底面圆的半径为多少米?
解:(1)∵∠BAC=90°,
∴BC为⊙O的直径,
即BC=米.
∴AB=BC=1米.
(2)设所得圆锥的底面圆的半径为r米,根据题意,得2πr=,解得r=.
∴底面圆的半径为米.
综合题
19.如图,点C为扇形OAB的半径OB上一点,将△OAC沿AC折叠,点O恰好落在上的点D处,且BDl∶ADl=1∶3(BDl表示的长).若将此扇形OAB围成一个圆锥,则圆锥的底面半径与母线长的比为(D)
A.1∶3 B.1∶π
C.1∶4 D.2∶9
20.如图是一纸杯,它的母线AC和EF延长后形成的立体图形是圆锥.该圆锥的侧面展开图形是扇形OAB.经测量,纸杯上开口圆的直径为6 cm,下底面圆的直径为4 cm,母线长EF=8 cm.
(1)求扇形OAB的圆心角;
(2)求这个纸杯的表面积(面积计算结果用π表示).
解:(1)由题意可知:
=6π cm,=4π cm.
设∠AOB=n°,AO=R cm,则CO=(R-8)cm,
由弧长公式得:=6π,=4π.
解方程组得
∴扇形OAB的圆心角是45°.
(2)∵R=24 cm,R-8=16 cm,
∴S扇形OCD=×4π×16=32π(cm2),
S扇形OAB=×6π×24=72π(cm2).
∴S纸杯侧面积=S扇形OAB-S扇形OCD=72π-32π=40π(cm2).
又∵S纸杯底面积=π×22=4π(cm2),
∴S纸杯表面积=40π+4π=44π(cm2).
