青岛版数学八年级下册8.1不等式的性质课件(34张)
文档属性
| 名称 | 青岛版数学八年级下册8.1不等式的性质课件(34张) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-22 00:00:00 | ||
图片预览











文档简介
(共34张PPT)
1、观察下面两组式子:
第一组: 1+2=3; a+b=b+a; S = ab; 4+x = 7.
第二组:-7 < -5; 3+4 > 1+4; 2x ≤6, a+2 ≥0;
3≠4.
第一组都是 ,第二组是 。
2、像-7 < -5; 3+4 > 1+4; 2x ≤6,a+2 ≥0; 3≠4等表示不等关系的式子叫做不等式
等式
不等式
知识点一: 不等式的定义
2 常见的不等号
一般地,用符号“<”(或“≤”)、“>”(或“≥”)、“≠”表示不等关系的式子叫做不等式。
“>”、“<”、“≥”、“≤”、“≠”
(1)-3<0; (2)4x+3y>0
(3)x=3; (4) X2+xy+y2
(5)x≠5; (6)X+2>y+5;
等式的两边都加上(或减去)同一个数或同一个整式,所得的结果仍是等式.
(2)等式的两边都乘以(或除以)同一个数(除数不能为零),所得的结果仍是等式.
若a=b,则a+c=b+c (或a-c=b-c)
知识回顾
等式的基本性质
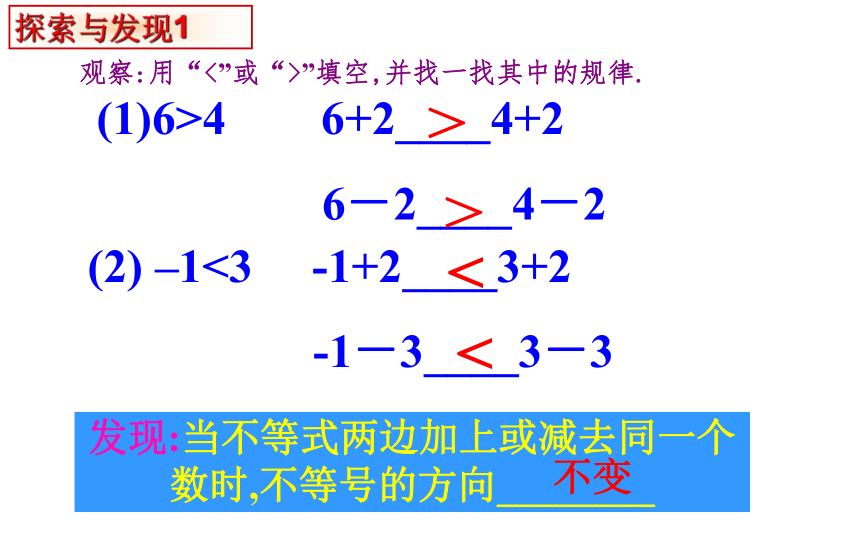
观察:用“<”或“>”填空,并找一找其中的规律.
(2) –1<3 -1+2____3+2
-1-3____3-3
6>4 6+2____4+2
6-2____4-2
>
>
<
<
发现:当不等式两边加上或减去同一个数时,不等号的方向________
不变
探索与发现1
不等式两边都加(或减去)
同一个数(或者同一个整式),不等号的方向不变.
根据不等式基本性质1
>
训练1: 用“>”或“<”填空:
(1)已知 a>b,则a+3 b+3;
(2)已知 a<
先前后比较
再定不等号
训练2: 1. 已知a < b,用“>”或“<”填空:
(1)a +x-2 b +x-2 ;
(2)a -y+6 b-y+6 .
<
<
已知4<6,则
4×2 6×2;
4÷2 6÷2;
<
<
探索与发现2
已知-4>-6,则
-4×2 -6×2;
-4÷2 -6÷2;
>
>
发现:不等式的两边都乘(或都除以)同一个正数,不等号的方向 。
不变
知识点三:
不等式的两边都乘(或都除以)同一个正数,不等号的方向不变。
如果a>b,且c>0,那么ac>bc
5___ -3
5× (-3) -3× (-3)
>
用“>”或“<”填空
由不等式“5>-3”做了怎样的变形?
不等式的两边都乘以了-3,
不等号改变方向
结果不等号的方向不变还是改变?
探索与发现3
<
-4÷(-4)____-2÷(-4)
结果不等号的方向不变还是改变?
再来试一试!
>
由不等式“-4 <-2”做了怎样的变形?
<
探索与发现3
不等号改变方向
探索与发现3
知识点四:
不等式的两边都乘以(或都除以)同一个负数,不等号的方向改变.
如果a>b,且c<0,那么ac<bc,
训练3: 用“>”或“<”填空:
(1)已知 a>b,则3a 3b ;
(2)已知 a>b,则-a -b .
不等式的性质1:不等式两边加上(或减去)同一个数(或整式),不等号的方向不变.
不等式的性质2:不等式两边乘以(或除以)同一个正数,不等号的方向不变.
不等式的性质3:不等式两边乘以(或除以)同一个负数,不等号的方向改变.
>
>
>
<
<
练一练
并说出这样填写的依据
先前后比较
再定不等号
判断对错并说明理由
2. 若 -3 × 2> -5 ×2, 则 -3< -5 ( )
3. 若 a4. 若 -6a < -6 b, 则 a < b ( )
×
√
×
用一用
(1) 若 x﹥y, 则 x - z ﹤ y - z ;
(3) 若 x﹥y, 则 x z 2 ﹥ y z 2 ;
×
×
5、
( )
( )
√
×
√
×
6. 若 a>b, 则-a < -b ( )
7. 若 -2x >0, 则 x > 0 ( )
8. 若 -2<1, 则 -2a < a ( )
9. 若 a >0, 则 3a > 2a ( )
判断对错并说明理由
用一用
当不等式两边都乘以(或除以)同 一个数时,一定要看清是正数还是负数;对于未给定范围的字母,应分情况讨论。
先前后比较
再定不等号
1.由xmy的条件是 ( )
A. m≥0 B. m≤0 C. m>0 D. m<0
D
2、若mx1,则应为 ( )
m<0 B. m>0 C. m≤0 D. m≥0
A
先前后比较
再定不等号
3、若axa<0 B. a>0 C. a≤0 D. a≥0
B
2.已知m(a-3)n,求a的范围.
1.已知x>y,比较2-3x与2-3y的大小.
先×(-3),再+2
先×(-3),再+2
×(a-3)
×(a-3)
<
>
先前后比较
再定不等号
解: 由题意可得:a-3<0(不等式的基本性质3)
∴a<3(不等式的基本性质2)
解 (1)根据不等式的性质1,两边都加上7得:
x-7+7 > 2+7
即 x > 9
(2)根据不等式的性质1,两边都减去5 x 得:
6 x -5 x <(5 x -1)-5 x
即 x <-1
例 1 根据不等式的基本性质,把下列不等式化成 x< 或 x> 的形式:
(1) x -7 > 2 (2) 6 x < 5 x -1
(3)4x-5< 5x (4) - x < -1
从变形前后的两个不等式可以看出,这种变形就是把不等式一边的某一项变号后移到另一边,我们把这种变形称为移项.
不等式的三条性质是:
① 、不等式的两边都加上(或减去)同一个 数或同一个整式,不等号的方向不变;
② 、不等式的两边都乘以(或除以)同一个 正数,不等号的方向不变;
③ 、*不等式的两边都乘以(或除以)同一个负数,不等号的方向要改变 ;
节本重点
(1)掌握不等式的三条性质,尤其是性质3;
(2)能正确应用性质对不等式进行变形;
zxxkw
选择适当的不等号填空,并说明理由。
(1)若a>b,则 .
(2)若a(3)若-a>-b,则-3a -3b.
(4)若-2x>-2y,则x y.
(5)若x达标检测
>
>
>
<
<
*
勇攀高峰:
选择适当的不等号填空,并说明理由。
(1)如果a(2)如果x<1,那么-2x+2 0.
(3)如果x(a-3)y,
那么a 3.
(4)如果a>
<
*
>
达标检测
不等式两边同除以正数2,得
还有什么方法?
还有什么方法?
练 习
1.用“>”或“<”号填空
(1)已知a>b,则3a____3b;
(2)已知a>b,则-a____-b;
(3)已知a>b,则-a+2____-b+2.
>
<
<
解: (1)根据不等式的性质1,两边都加上5得:
即:
x-5+5 >-1+5
(2)根据不等式的性质3,两边都除以-2 得:
即 :x>4
1.由xmy的条件是 ( )
A. m≥0 B. m≤0 C. m>0 D. m<0
D
2、若mx1,则应为 ( )
m<0 B. m>0 C. m≤0 D. m≥0
A
5: 若x>y,且(a-3)x<(a-3)y,求a的取值范围。
3.已知x>y,比较2-3x与2-3y的大小.
4:已知x>y,
先前后比较
再定不等号
>
>
>
<
1
2
3
1
1、观察下面两组式子:
第一组: 1+2=3; a+b=b+a; S = ab; 4+x = 7.
第二组:-7 < -5; 3+4 > 1+4; 2x ≤6, a+2 ≥0;
3≠4.
第一组都是 ,第二组是 。
2、像-7 < -5; 3+4 > 1+4; 2x ≤6,a+2 ≥0; 3≠4等表示不等关系的式子叫做不等式
等式
不等式
知识点一: 不等式的定义
2 常见的不等号
一般地,用符号“<”(或“≤”)、“>”(或“≥”)、“≠”表示不等关系的式子叫做不等式。
“>”、“<”、“≥”、“≤”、“≠”
(1)-3<0; (2)4x+3y>0
(3)x=3; (4) X2+xy+y2
(5)x≠5; (6)X+2>y+5;
等式的两边都加上(或减去)同一个数或同一个整式,所得的结果仍是等式.
(2)等式的两边都乘以(或除以)同一个数(除数不能为零),所得的结果仍是等式.
若a=b,则a+c=b+c (或a-c=b-c)
知识回顾
等式的基本性质
观察:用“<”或“>”填空,并找一找其中的规律.
(2) –1<3 -1+2____3+2
-1-3____3-3
6>4 6+2____4+2
6-2____4-2
>
>
<
<
发现:当不等式两边加上或减去同一个数时,不等号的方向________
不变
探索与发现1
不等式两边都加(或减去)
同一个数(或者同一个整式),不等号的方向不变.
根据不等式基本性质1
>
训练1: 用“>”或“<”填空:
(1)已知 a>b,则a+3 b+3;
(2)已知 a
先前后比较
再定不等号
训练2: 1. 已知a < b,用“>”或“<”填空:
(1)a +x-2 b +x-2 ;
(2)a -y+6 b-y+6 .
<
<
已知4<6,则
4×2 6×2;
4÷2 6÷2;
<
<
探索与发现2
已知-4>-6,则
-4×2 -6×2;
-4÷2 -6÷2;
>
>
发现:不等式的两边都乘(或都除以)同一个正数,不等号的方向 。
不变
知识点三:
不等式的两边都乘(或都除以)同一个正数,不等号的方向不变。
如果a>b,且c>0,那么ac>bc
5___ -3
5× (-3) -3× (-3)
>
用“>”或“<”填空
由不等式“5>-3”做了怎样的变形?
不等式的两边都乘以了-3,
不等号改变方向
结果不等号的方向不变还是改变?
探索与发现3
<
-4÷(-4)____-2÷(-4)
结果不等号的方向不变还是改变?
再来试一试!
>
由不等式“-4 <-2”做了怎样的变形?
<
探索与发现3
不等号改变方向
探索与发现3
知识点四:
不等式的两边都乘以(或都除以)同一个负数,不等号的方向改变.
如果a>b,且c<0,那么ac<bc,
训练3: 用“>”或“<”填空:
(1)已知 a>b,则3a 3b ;
(2)已知 a>b,则-a -b .
不等式的性质1:不等式两边加上(或减去)同一个数(或整式),不等号的方向不变.
不等式的性质2:不等式两边乘以(或除以)同一个正数,不等号的方向不变.
不等式的性质3:不等式两边乘以(或除以)同一个负数,不等号的方向改变.
>
>
>
<
<
练一练
并说出这样填写的依据
先前后比较
再定不等号
判断对错并说明理由
2. 若 -3 × 2> -5 ×2, 则 -3< -5 ( )
3. 若 a
×
√
×
用一用
(1) 若 x﹥y, 则 x - z ﹤ y - z ;
(3) 若 x﹥y, 则 x z 2 ﹥ y z 2 ;
×
×
5、
( )
( )
√
×
√
×
6. 若 a>b, 则-a < -b ( )
7. 若 -2x >0, 则 x > 0 ( )
8. 若 -2<1, 则 -2a < a ( )
9. 若 a >0, 则 3a > 2a ( )
判断对错并说明理由
用一用
当不等式两边都乘以(或除以)同 一个数时,一定要看清是正数还是负数;对于未给定范围的字母,应分情况讨论。
先前后比较
再定不等号
1.由x
A. m≥0 B. m≤0 C. m>0 D. m<0
D
2、若mx
m<0 B. m>0 C. m≤0 D. m≥0
A
先前后比较
再定不等号
3、若ax
B
2.已知m
1.已知x>y,比较2-3x与2-3y的大小.
先×(-3),再+2
先×(-3),再+2
×(a-3)
×(a-3)
<
>
先前后比较
再定不等号
解: 由题意可得:a-3<0(不等式的基本性质3)
∴a<3(不等式的基本性质2)
解 (1)根据不等式的性质1,两边都加上7得:
x-7+7 > 2+7
即 x > 9
(2)根据不等式的性质1,两边都减去5 x 得:
6 x -5 x <(5 x -1)-5 x
即 x <-1
例 1 根据不等式的基本性质,把下列不等式化成 x< 或 x> 的形式:
(1) x -7 > 2 (2) 6 x < 5 x -1
(3)4x-5< 5x (4) - x < -1
从变形前后的两个不等式可以看出,这种变形就是把不等式一边的某一项变号后移到另一边,我们把这种变形称为移项.
不等式的三条性质是:
① 、不等式的两边都加上(或减去)同一个 数或同一个整式,不等号的方向不变;
② 、不等式的两边都乘以(或除以)同一个 正数,不等号的方向不变;
③ 、*不等式的两边都乘以(或除以)同一个负数,不等号的方向要改变 ;
节本重点
(1)掌握不等式的三条性质,尤其是性质3;
(2)能正确应用性质对不等式进行变形;
zxxkw
选择适当的不等号填空,并说明理由。
(1)若a>b,则 .
(2)若a
(4)若-2x>-2y,则x y.
(5)若x
>
>
>
<
<
*
勇攀高峰:
选择适当的不等号填空,并说明理由。
(1)如果a
(3)如果x
那么a 3.
(4)如果a
<
*
>
达标检测
不等式两边同除以正数2,得
还有什么方法?
还有什么方法?
练 习
1.用“>”或“<”号填空
(1)已知a>b,则3a____3b;
(2)已知a>b,则-a____-b;
(3)已知a>b,则-a+2____-b+2.
>
<
<
解: (1)根据不等式的性质1,两边都加上5得:
即:
x-5+5 >-1+5
(2)根据不等式的性质3,两边都除以-2 得:
即 :x>4
1.由x
A. m≥0 B. m≤0 C. m>0 D. m<0
D
2、若mx
m<0 B. m>0 C. m≤0 D. m≥0
A
5: 若x>y,且(a-3)x<(a-3)y,求a的取值范围。
3.已知x>y,比较2-3x与2-3y的大小.
4:已知x>y,
先前后比较
再定不等号
>
>
>
<
1
2
3
1
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
