沪科版数学八年级下册18.1勾股定理学案(共4课时、无答案)
文档属性
| 名称 | 沪科版数学八年级下册18.1勾股定理学案(共4课时、无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-22 17:44:13 | ||
图片预览


文档简介
18.1.1 勾股定理(第一课时)
【学习目标】1了解勾股定理的发现过程,掌握勾股定理的内容,会用面积法证明勾股定理。
2培养在实际生活中发现问题总结规律的意识和能力。
3介绍我国古代在勾股定理研究方面所取得的成就,激发学生的爱国热情。
【重点难点】重点:勾股定理的内容及证明。
难点:勾股定理的证明。
【课前自主学习1】填空:已知一Rt△ABC,∠C=90°(1)∠A=80°,则∠B= ;
(2)∠A=30°,c=6cm,则∠B= ,a= 、(3) ∠A=45°,a=2cm,则∠B= ,b=
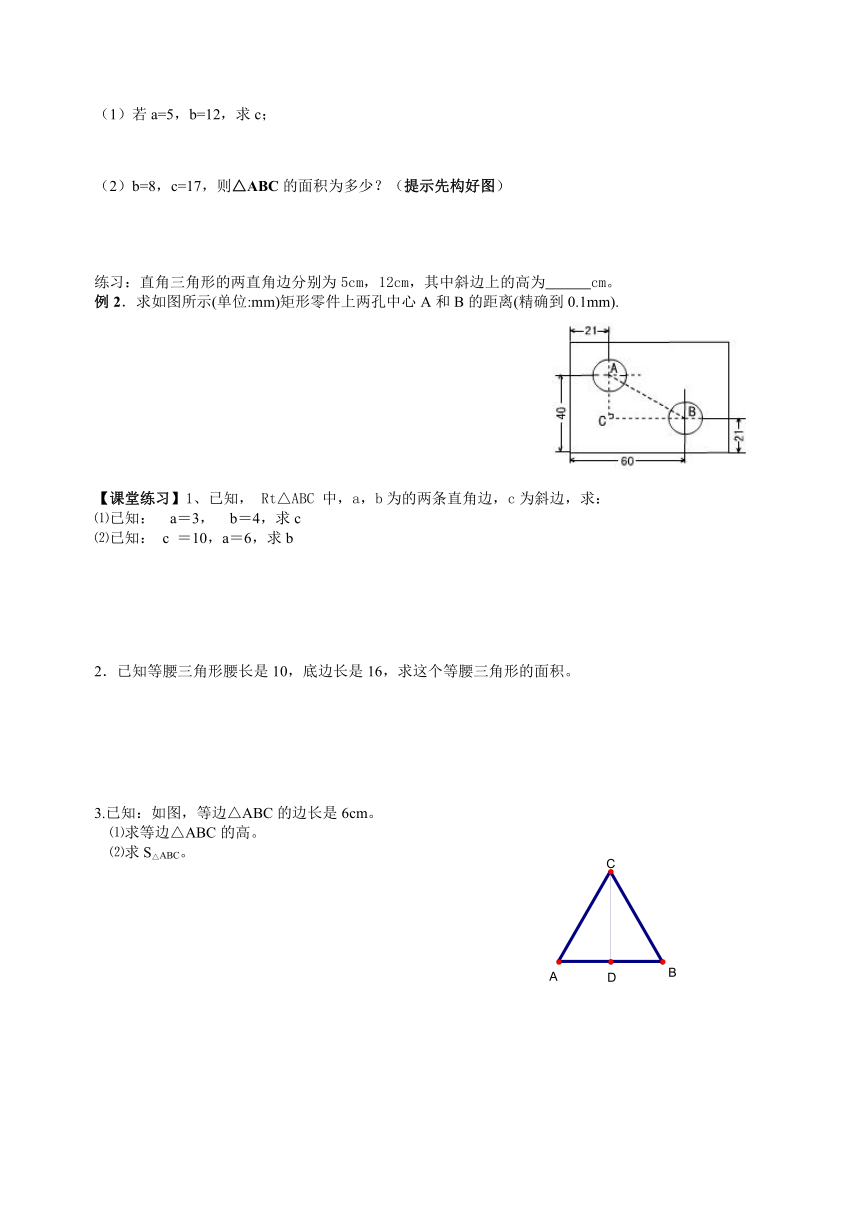
【课前自主学2】如图,剪4个全等的直角三角拼成如图的图形:则正方形的面积表示为 ;正方形的面积还可表示为 由此你能得到此直角三角形三边a、b、c之间存在的等量关系式为
图1
【师生交流】公元前572前492年古希腊著名的哲学家、数学家、天文学家毕达哥拉斯,他在一次朋友家做客时,发现朋友家用砖铺成的地面中用了直角三角形三边的某种数量关系,请同学们一起来观察图2中的地面,你能发现什么呢?
1. 你能用三角形的三边长a、b、c表示正方形1、正方形2、正方形3的面积吗?
答:正方形1的面积 ,正方形2的面积 正方形3的面积
2. 你能发现直角三角形两直角边a、b与斜边c之间存在什么关系吗?
答:
【探究总结】
1.图1-1中,正方形A中含有 个小方格,即A的面积是 单位面积,B的面积是
单位面积,C的面积是 单位面积.
2. .图1-2中,正方形A中含有 个小方格,即A的面积是 单位面积,B的面积
单位面积,C的面积是 单位面积.
3.图1-3中,正方形A中含有 个小方格,即A的面积是 单位面积,B的面积是
单位面积,C的面积是 单位面积.
4.图1-4中,正方形A中含有 个小方格,即A的面积是 单位面积,B的面积是
单位面积,C的面积是 单位面积.
总结:由上图中三正方形面积存在的等量关系式为 ;若设所围成的直角三角形两直角边a、b为斜边为c,则三边存在的等量关系式为 ,此定理我们称为勾股定理。
【例题讲解】例 1。在Rt△ABC中,∠C=90°
(1)若a=5,b=12,求c;
(2)b=8,c=17,则△ABC的面积为多少?(提示先构好图)
练习:直角三角形的两直角边分别为5cm,12cm,其中斜边上的高为 cm。
例2.求如图所示(单位:mm)矩形零件上两孔中心A和B的距离(精确到0.1mm).
【课堂练习】1、已知, Rt△ABC 中,a,b为的两条直角边,c为斜边,求:
⑴已知: a=3, b=4,求c
⑵已知: c =10,a=6,求b
2.已知等腰三角形腰长是10,底边长是16,求这个等腰三角形的面积。
3.已知:如图,等边△ABC的边长是6cm。
⑴求等边△ABC的高。
⑵求S△ABC。
18.1.2 勾股定理(第二课时)
【学习目标】1.会用勾股定理进行简单的计算。
2.运用勾股定理解释生活中的实际问题。
3培养在实际生活中发现问题总结规律的意识和能力。
【重点难点】重点:勾股定理的实际应用。
难点:勾股定理在实际生活中的应用。
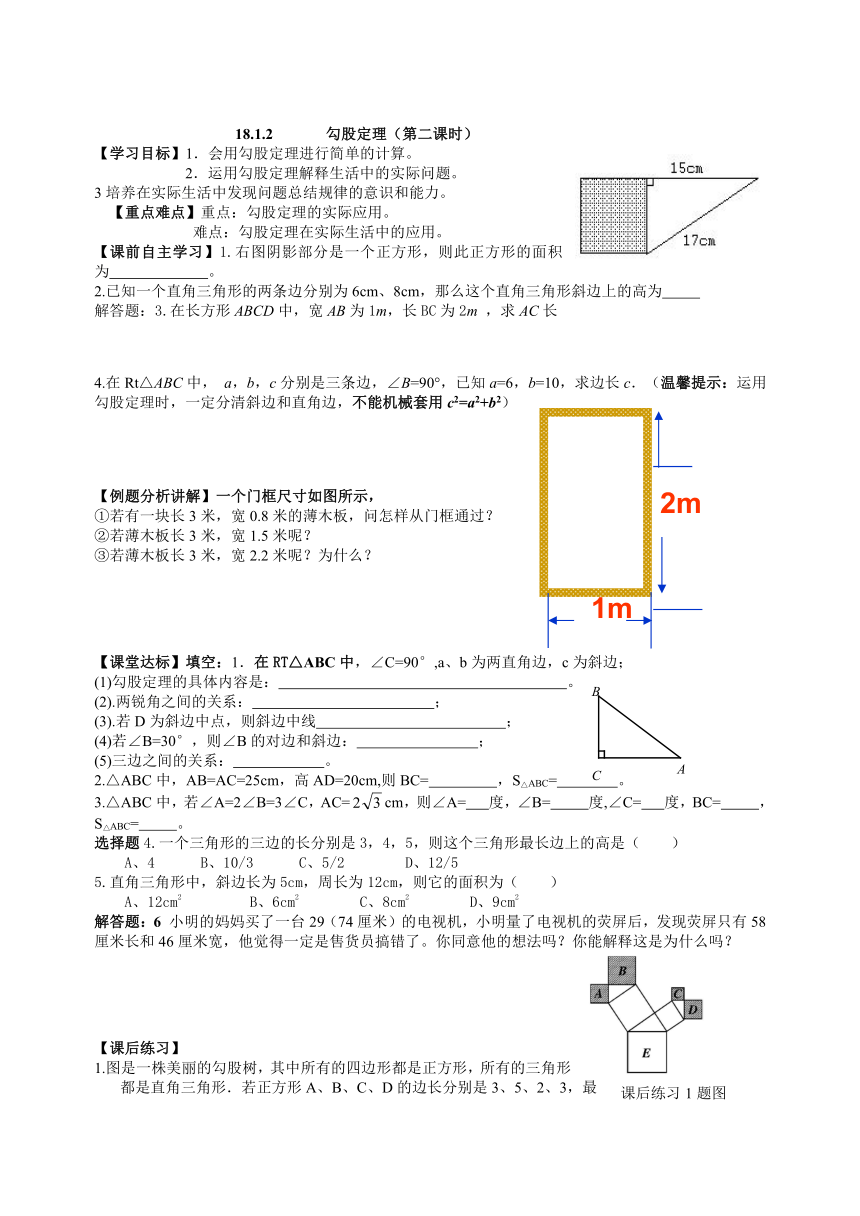
【课前自主学习】1.右图阴影部分是一个正方形,则此正方形的面积为 。
2.已知一个直角三角形的两条边分别为6cm、8cm,那么这个直角三角形斜边上的高为
解答题:3.在长方形ABCD中,宽AB为1m,长BC为2m ,求AC长
4.在Rt△ABC中, a,b,c分别是三条边,∠B=90°,已知a=6,b=10,求边长c.(温馨提示:运用勾股定理时,一定分清斜边和直角边,不能机械套用c2=a2+b2)
【例题分析讲解】一个门框尺寸如图所示,
①若有一块长3米,宽0.8米的薄木板,问怎样从门框通过?
②若薄木板长3米,宽1.5米呢?
③若薄木板长3米,宽2.2米呢?为什么?
【课堂达标】填空:1.在RT△ABC中,∠C=90°,a、b为两直角边,c为斜边;
(1)勾股定理的具体内容是: 。
(2).两锐角之间的关系: ;
(3).若D为斜边中点,则斜边中线 ;
(4)若∠B=30°,则∠B的对边和斜边: ;
(5)三边之间的关系: 。
2.△ABC中,AB=AC=25cm,高AD=20cm,则BC= ,S△ABC= 。
3.△ABC中,若∠A=2∠B=3∠C,AC=cm,则∠A= 度,∠B= 度,∠C= 度,BC= ,S△ABC= 。
选择题4.一个三角形的三边的长分别是3,4,5,则这个三角形最长边上的高是( )
A、4 B、10/3 C、5/2 D、12/5
5.直角三角形中,斜边长为5cm,周长为12cm,则它的面积为( )
A、12cm2 B、6cm2 C、8cm2 D、9cm2
解答题:6 小明的妈妈买了一台29(74厘米)的电视机,小明量了电视机的荧屏后,发现荧屏只有58厘米长和46厘米宽,他觉得一定是售货员搞错了。你同意他的想法吗?你能解释这是为什么吗?
【课后练习】
1.图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A、B、C、D的边长分别是3、5、2、3,最大正方形E的面积是( )
A.13 B.26 C.47 D.94
2.已知△ABC中,∠A= 2∠B= 3∠C,则它的三条边之比为(? ).
??? A.1:1:2 ??? B.1: :2??? C.1: :2 ??? D.1:4:1
3.已知直角三角形一个锐角60°,斜边长为1,那么此直角三角形的周长是 .
4.直角三角形的两条直角边分别是5cm,12cm,其斜边上的高是__________
5.已知直角三角形的两边长为3、2,则另一条边长________________.
6.甲船以10海里/小时的速度从港口向北航行,乙船以20海里/小时的速度从港口向东航行,同时行驶3小时后乙遇险,甲调转航向前去抢救,船长想知道两地间的距离,你能帮忙算一下吗?
7、已知:如图,△ABC中,AC=4,∠B=45°,∠A=60°,根据题设可知什么?.如图,∠B=∠D=90°,∠A=60°,AB=4,CD=2。求:四边形ABCD的面积。
8、四边形ABCD如图所示,请计算其面积.
18.1.3 勾股定理(第三课时)
【学习目标】1.会用勾股定理进行简单的计算。
2.运用勾股定理解释生活中的实际问题。
【重点难点】重点:勾股定理的应用。
难点:勾股定理在实际生活中的应用。
【课前自主学习】1.在Rt△ABC,∠C=90°
⑴已知a=b=5,求c; ⑵已知a=1,c=2, 求b;
(3)已知a:b=1:2,c=5, 求a; (4)已知b=15,∠A=30°,求a,c
2.在Rt中,已知两边长为3、4,求第三边的长.
【例题分析讲解】一个3m长的梯子BE斜靠在一竖直的墙AE上,这时AE的距离为2.5m.如果梯子顶端E沿墙下滑0.5m,那么梯子底端B也外移0.5m吗?
分析:1.B点是否外移0.5m,可以算出 的长来比较。
2.在 中,可利用勾股定理计算出AB的长,AB=
3.已知AE= ,DE= ,可得AD=
4.在 中,可利用勾股定理计算出AC的长,AC=
解:
练习.已知:如图,在△ABC中,∠C=60°,AB=,AC=4,AD是BC边上的高,求BC的长。
【课堂达标】填空:1.已知直角三角形的两边长分别为3cm和5cm,,则第三边长为 。
2.已知等边三角形的边长为2cm,则它的高为 ,面积为
3.小明和爸爸妈妈十一登香山,他们沿着45度的坡路走了500米,看到了一棵红叶树,这棵红叶树的离地面的高度是 米。
4.如图,欲测量松花江的宽度,沿江岸取B、C两点,
在江对岸取一点A,使AC垂直江岸,测得BC=50米,∠B=60°,则江面的宽度为 。
解答题:池塘边有两点A、B,点C是与BA方向成直角的
AC方向上一点,测得CB=60m,AC=20m。你能求出
A、B两点间的距离吗?(结果保留整数)
【课后练习】1.如图1:一根32厘米的绳子被折成如图所示的形状钉在P、Q两点,PQ=16厘米,且RP⊥PQ,则RQ= 厘米。
2.如图2,分别以Rt △ABC三边为边向外作三个圆,其面积分别用S1、S2、S3表示,容易得出S1、S2、S3之间有的关系式 .
3.如图,钢索斜拉大桥为等腰三角形,支柱高24米,∠B=∠C=30°,E、F分别为BD、CD中点,试求B、C两点之间的距离,钢索AB和AE的长度。
(精确到1米)
4.已知等腰三角形腰长是10,底边长是16,求这个等腰三角形的面积。
5、如图所示,在四边形ABCD中,AB=AD=8,∠A=60°,∠ADC=150°,已知四边形ABCD的周长为32,求四边形ABCD的面积
18.1.4勾股定理(第四课时)
【学习目标】1会利用勾股定理在数轴上表示一个无理数。
2.通过构造直角三角形解决实际问题。
难点:构造直角三角形巧用勾股定理。
【课前自主学习1】请先动手制作一个圆柱体以供例1使用!
填空:1.已知直角三角形ABC的三边为a、b、c,∠C= 90°则 a,b,c 三者之间的关系为 ;
2.矩形的一边长是5,对角线是13,则它的面积是 ;
解答题:3.若一个直角三角形两条直角边长是3和2,那么第三条边长是多少?
4、如图,在一块形状为直角梯形的草坪边上,修建了一条由A→D→C的小路.一些路人为了走“捷径”,沿线段AC行走,破坏了草坪,但实际上他们仅少走了_______m.
【课前自主学习2】1.数轴上的点与 是 一 一对应的关系。A实数 B有理数 C无理数
2.你能在数轴上画出表示与的点吗?
【师生交流】利用在数轴上构造一个以所求无理数的长为斜边的直角三角形的方法,你能否在数轴上画出表示的点吗?
分析:1. + = + = + = + = + = + = + =。。。。
2.由1可推知长为的线段是直角边为正整数 和 的直角三角形的斜边;
3.那么可在数轴上找到一点A,使得OA= ,再过 点作垂直于x轴的垂线m,,在m上
截取AB= ,连接OB,以 为圆心,以 为半径作弧,弧与数轴的交点C表示为。
4.你能在数轴上表示的点吗?试一试!
【例题讲解】例1.为筹备迎新生晚会,同学们设计了一个圆筒形灯罩,底色漆成白色,然后缠绕红色油纸,如图3(1),已知圆筒高108㎝,其截面周长为36㎝,如果在表面缠绕油纸4圈,应裁剪多长油纸.
【课堂练习】1如图一个圆柱,底圆周长6cm,高4cm,一只蚂蚁沿外壁爬行,要从A点爬到B点,则最少要爬多长?
2.如图,某学校(A点)与公路(直线L)的距离为300米,又与公路车站(D点)的距离为500米,现要在公路上建一个小商店(C点),使之与该校A及车站D的距离相等,求商店与车站之间的距离.
3、一个长为10m的梯子斜靠在墙上,梯子底端距墙底6m.
(1)若梯子的底端水平向外滑动1m,梯子的顶端下滑多少米?
(2)如果梯子顶端向下滑动的距离等于底端向外滑动的距离,那么滑动的距离是多少米?
图2
2m
1m
A
C
B
课后练习1题图
60
C
20
A
B
S1
S2
S3
图2
图1
图3(1)
【学习目标】1了解勾股定理的发现过程,掌握勾股定理的内容,会用面积法证明勾股定理。
2培养在实际生活中发现问题总结规律的意识和能力。
3介绍我国古代在勾股定理研究方面所取得的成就,激发学生的爱国热情。
【重点难点】重点:勾股定理的内容及证明。
难点:勾股定理的证明。
【课前自主学习1】填空:已知一Rt△ABC,∠C=90°(1)∠A=80°,则∠B= ;
(2)∠A=30°,c=6cm,则∠B= ,a= 、(3) ∠A=45°,a=2cm,则∠B= ,b=
【课前自主学2】如图,剪4个全等的直角三角拼成如图的图形:则正方形的面积表示为 ;正方形的面积还可表示为 由此你能得到此直角三角形三边a、b、c之间存在的等量关系式为
图1
【师生交流】公元前572前492年古希腊著名的哲学家、数学家、天文学家毕达哥拉斯,他在一次朋友家做客时,发现朋友家用砖铺成的地面中用了直角三角形三边的某种数量关系,请同学们一起来观察图2中的地面,你能发现什么呢?
1. 你能用三角形的三边长a、b、c表示正方形1、正方形2、正方形3的面积吗?
答:正方形1的面积 ,正方形2的面积 正方形3的面积
2. 你能发现直角三角形两直角边a、b与斜边c之间存在什么关系吗?
答:
【探究总结】
1.图1-1中,正方形A中含有 个小方格,即A的面积是 单位面积,B的面积是
单位面积,C的面积是 单位面积.
2. .图1-2中,正方形A中含有 个小方格,即A的面积是 单位面积,B的面积
单位面积,C的面积是 单位面积.
3.图1-3中,正方形A中含有 个小方格,即A的面积是 单位面积,B的面积是
单位面积,C的面积是 单位面积.
4.图1-4中,正方形A中含有 个小方格,即A的面积是 单位面积,B的面积是
单位面积,C的面积是 单位面积.
总结:由上图中三正方形面积存在的等量关系式为 ;若设所围成的直角三角形两直角边a、b为斜边为c,则三边存在的等量关系式为 ,此定理我们称为勾股定理。
【例题讲解】例 1。在Rt△ABC中,∠C=90°
(1)若a=5,b=12,求c;
(2)b=8,c=17,则△ABC的面积为多少?(提示先构好图)
练习:直角三角形的两直角边分别为5cm,12cm,其中斜边上的高为 cm。
例2.求如图所示(单位:mm)矩形零件上两孔中心A和B的距离(精确到0.1mm).
【课堂练习】1、已知, Rt△ABC 中,a,b为的两条直角边,c为斜边,求:
⑴已知: a=3, b=4,求c
⑵已知: c =10,a=6,求b
2.已知等腰三角形腰长是10,底边长是16,求这个等腰三角形的面积。
3.已知:如图,等边△ABC的边长是6cm。
⑴求等边△ABC的高。
⑵求S△ABC。
18.1.2 勾股定理(第二课时)
【学习目标】1.会用勾股定理进行简单的计算。
2.运用勾股定理解释生活中的实际问题。
3培养在实际生活中发现问题总结规律的意识和能力。
【重点难点】重点:勾股定理的实际应用。
难点:勾股定理在实际生活中的应用。
【课前自主学习】1.右图阴影部分是一个正方形,则此正方形的面积为 。
2.已知一个直角三角形的两条边分别为6cm、8cm,那么这个直角三角形斜边上的高为
解答题:3.在长方形ABCD中,宽AB为1m,长BC为2m ,求AC长
4.在Rt△ABC中, a,b,c分别是三条边,∠B=90°,已知a=6,b=10,求边长c.(温馨提示:运用勾股定理时,一定分清斜边和直角边,不能机械套用c2=a2+b2)
【例题分析讲解】一个门框尺寸如图所示,
①若有一块长3米,宽0.8米的薄木板,问怎样从门框通过?
②若薄木板长3米,宽1.5米呢?
③若薄木板长3米,宽2.2米呢?为什么?
【课堂达标】填空:1.在RT△ABC中,∠C=90°,a、b为两直角边,c为斜边;
(1)勾股定理的具体内容是: 。
(2).两锐角之间的关系: ;
(3).若D为斜边中点,则斜边中线 ;
(4)若∠B=30°,则∠B的对边和斜边: ;
(5)三边之间的关系: 。
2.△ABC中,AB=AC=25cm,高AD=20cm,则BC= ,S△ABC= 。
3.△ABC中,若∠A=2∠B=3∠C,AC=cm,则∠A= 度,∠B= 度,∠C= 度,BC= ,S△ABC= 。
选择题4.一个三角形的三边的长分别是3,4,5,则这个三角形最长边上的高是( )
A、4 B、10/3 C、5/2 D、12/5
5.直角三角形中,斜边长为5cm,周长为12cm,则它的面积为( )
A、12cm2 B、6cm2 C、8cm2 D、9cm2
解答题:6 小明的妈妈买了一台29(74厘米)的电视机,小明量了电视机的荧屏后,发现荧屏只有58厘米长和46厘米宽,他觉得一定是售货员搞错了。你同意他的想法吗?你能解释这是为什么吗?
【课后练习】
1.图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A、B、C、D的边长分别是3、5、2、3,最大正方形E的面积是( )
A.13 B.26 C.47 D.94
2.已知△ABC中,∠A= 2∠B= 3∠C,则它的三条边之比为(? ).
??? A.1:1:2 ??? B.1: :2??? C.1: :2 ??? D.1:4:1
3.已知直角三角形一个锐角60°,斜边长为1,那么此直角三角形的周长是 .
4.直角三角形的两条直角边分别是5cm,12cm,其斜边上的高是__________
5.已知直角三角形的两边长为3、2,则另一条边长________________.
6.甲船以10海里/小时的速度从港口向北航行,乙船以20海里/小时的速度从港口向东航行,同时行驶3小时后乙遇险,甲调转航向前去抢救,船长想知道两地间的距离,你能帮忙算一下吗?
7、已知:如图,△ABC中,AC=4,∠B=45°,∠A=60°,根据题设可知什么?.如图,∠B=∠D=90°,∠A=60°,AB=4,CD=2。求:四边形ABCD的面积。
8、四边形ABCD如图所示,请计算其面积.
18.1.3 勾股定理(第三课时)
【学习目标】1.会用勾股定理进行简单的计算。
2.运用勾股定理解释生活中的实际问题。
【重点难点】重点:勾股定理的应用。
难点:勾股定理在实际生活中的应用。
【课前自主学习】1.在Rt△ABC,∠C=90°
⑴已知a=b=5,求c; ⑵已知a=1,c=2, 求b;
(3)已知a:b=1:2,c=5, 求a; (4)已知b=15,∠A=30°,求a,c
2.在Rt中,已知两边长为3、4,求第三边的长.
【例题分析讲解】一个3m长的梯子BE斜靠在一竖直的墙AE上,这时AE的距离为2.5m.如果梯子顶端E沿墙下滑0.5m,那么梯子底端B也外移0.5m吗?
分析:1.B点是否外移0.5m,可以算出 的长来比较。
2.在 中,可利用勾股定理计算出AB的长,AB=
3.已知AE= ,DE= ,可得AD=
4.在 中,可利用勾股定理计算出AC的长,AC=
解:
练习.已知:如图,在△ABC中,∠C=60°,AB=,AC=4,AD是BC边上的高,求BC的长。
【课堂达标】填空:1.已知直角三角形的两边长分别为3cm和5cm,,则第三边长为 。
2.已知等边三角形的边长为2cm,则它的高为 ,面积为
3.小明和爸爸妈妈十一登香山,他们沿着45度的坡路走了500米,看到了一棵红叶树,这棵红叶树的离地面的高度是 米。
4.如图,欲测量松花江的宽度,沿江岸取B、C两点,
在江对岸取一点A,使AC垂直江岸,测得BC=50米,∠B=60°,则江面的宽度为 。
解答题:池塘边有两点A、B,点C是与BA方向成直角的
AC方向上一点,测得CB=60m,AC=20m。你能求出
A、B两点间的距离吗?(结果保留整数)
【课后练习】1.如图1:一根32厘米的绳子被折成如图所示的形状钉在P、Q两点,PQ=16厘米,且RP⊥PQ,则RQ= 厘米。
2.如图2,分别以Rt △ABC三边为边向外作三个圆,其面积分别用S1、S2、S3表示,容易得出S1、S2、S3之间有的关系式 .
3.如图,钢索斜拉大桥为等腰三角形,支柱高24米,∠B=∠C=30°,E、F分别为BD、CD中点,试求B、C两点之间的距离,钢索AB和AE的长度。
(精确到1米)
4.已知等腰三角形腰长是10,底边长是16,求这个等腰三角形的面积。
5、如图所示,在四边形ABCD中,AB=AD=8,∠A=60°,∠ADC=150°,已知四边形ABCD的周长为32,求四边形ABCD的面积
18.1.4勾股定理(第四课时)
【学习目标】1会利用勾股定理在数轴上表示一个无理数。
2.通过构造直角三角形解决实际问题。
难点:构造直角三角形巧用勾股定理。
【课前自主学习1】请先动手制作一个圆柱体以供例1使用!
填空:1.已知直角三角形ABC的三边为a、b、c,∠C= 90°则 a,b,c 三者之间的关系为 ;
2.矩形的一边长是5,对角线是13,则它的面积是 ;
解答题:3.若一个直角三角形两条直角边长是3和2,那么第三条边长是多少?
4、如图,在一块形状为直角梯形的草坪边上,修建了一条由A→D→C的小路.一些路人为了走“捷径”,沿线段AC行走,破坏了草坪,但实际上他们仅少走了_______m.
【课前自主学习2】1.数轴上的点与 是 一 一对应的关系。A实数 B有理数 C无理数
2.你能在数轴上画出表示与的点吗?
【师生交流】利用在数轴上构造一个以所求无理数的长为斜边的直角三角形的方法,你能否在数轴上画出表示的点吗?
分析:1. + = + = + = + = + = + = + =。。。。
2.由1可推知长为的线段是直角边为正整数 和 的直角三角形的斜边;
3.那么可在数轴上找到一点A,使得OA= ,再过 点作垂直于x轴的垂线m,,在m上
截取AB= ,连接OB,以 为圆心,以 为半径作弧,弧与数轴的交点C表示为。
4.你能在数轴上表示的点吗?试一试!
【例题讲解】例1.为筹备迎新生晚会,同学们设计了一个圆筒形灯罩,底色漆成白色,然后缠绕红色油纸,如图3(1),已知圆筒高108㎝,其截面周长为36㎝,如果在表面缠绕油纸4圈,应裁剪多长油纸.
【课堂练习】1如图一个圆柱,底圆周长6cm,高4cm,一只蚂蚁沿外壁爬行,要从A点爬到B点,则最少要爬多长?
2.如图,某学校(A点)与公路(直线L)的距离为300米,又与公路车站(D点)的距离为500米,现要在公路上建一个小商店(C点),使之与该校A及车站D的距离相等,求商店与车站之间的距离.
3、一个长为10m的梯子斜靠在墙上,梯子底端距墙底6m.
(1)若梯子的底端水平向外滑动1m,梯子的顶端下滑多少米?
(2)如果梯子顶端向下滑动的距离等于底端向外滑动的距离,那么滑动的距离是多少米?
图2
2m
1m
A
C
B
课后练习1题图
60
C
20
A
B
S1
S2
S3
图2
图1
图3(1)
