2020春冀教版八下数学22.2平行四边形的判断课件(15张)
文档属性
| 名称 | 2020春冀教版八下数学22.2平行四边形的判断课件(15张) |

|
|
| 格式 | zip | ||
| 文件大小 | 378.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-22 17:35:23 | ||
图片预览




文档简介
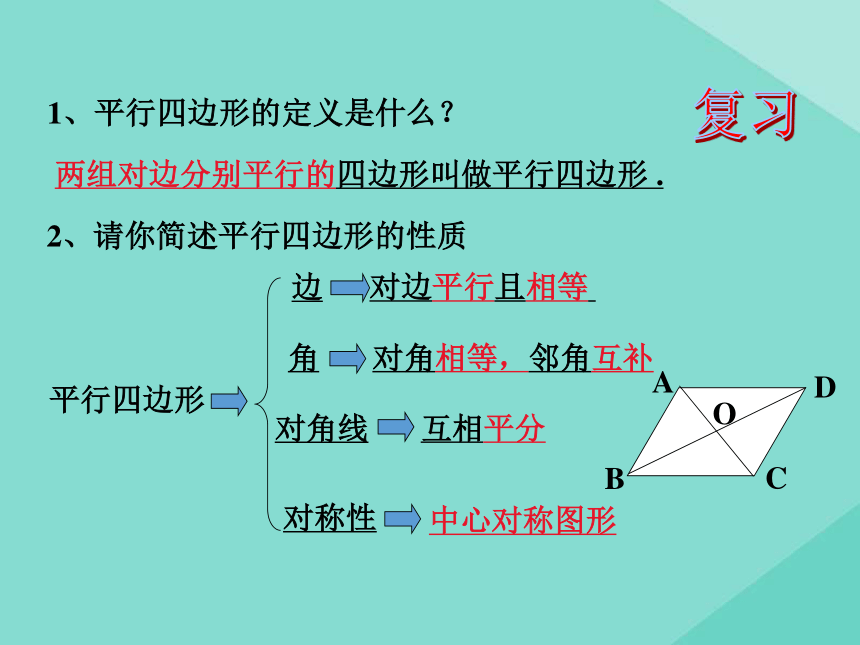
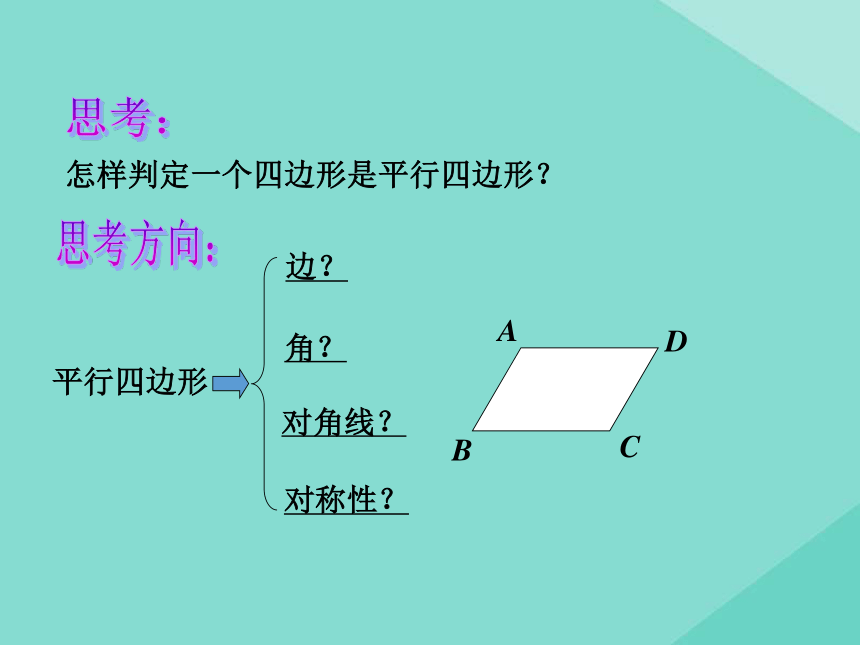
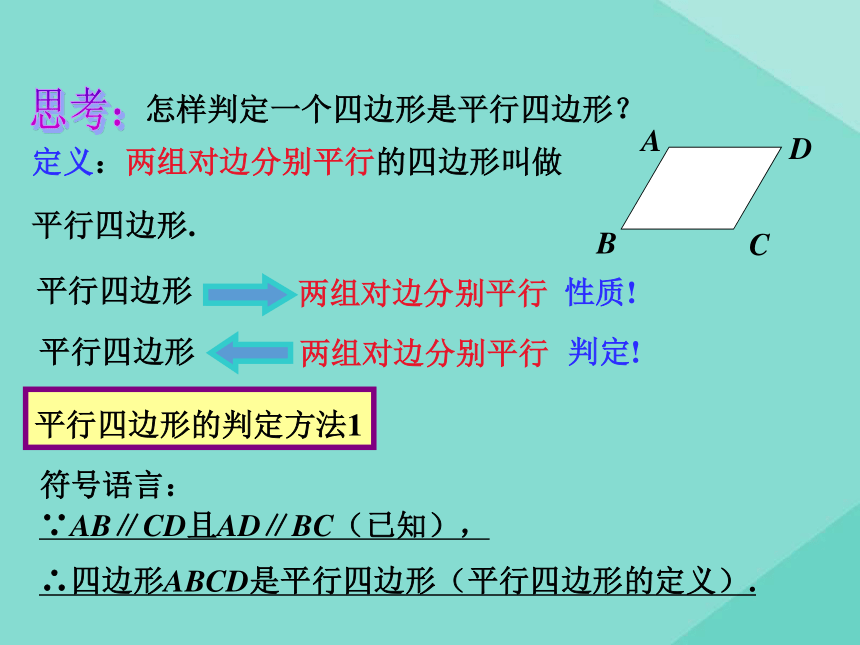
课件15张PPT。教学课件数学 八年级下册 冀教版第二十二章 四边形22.2 平行四边形的判定1、平行四边形的定义是什么?两组对边分别平行的四边形叫做平行四边形 .互相平分平行四边形边角对角线对角相等,邻角互补对称性中心对称图形2、请你简述平行四边形的性质对边平行且相等 复习观察阅读:结论:四边形不具有稳定性;三角形具有稳定性.思考方向:怎样判定一个四边形是平行四边形?思考:平行四边形边?角?对角线?对称性?怎样判定一个四边形是平行四边形?定义:两组对边分别平行的四边形叫做
平行四边形.思考:∵AB∥CD且AD∥BC(已知),
∴四边形ABCD是平行四边形(平行四边形的定义).符号语言:平行四边形的判定方法1平行四边形两组对边分别平行性质!两组对边分别平行平行四边形判定! 通过前面的学习,我们知道,平行四边形的对边相等、对角相等、对角线互相平分,那么这些命题的逆命题成立吗??思考两组对边分别相等的四边形是平行四边形.已知:四边形ABCD中,AB=CD, AD=BC. 求证:四边形ABCD是平行四边形. 从边出发:判定定理1 (判定方法2):
证明:连接AC∴△ABC≌△CDA(SSS).∵ AB=CD,AD=CB,AC=CA,∴∠CAB=∠ACD,∠ACB= ∠CAD,∴AB//CD,AD//BC,∴四边形ABCD是平行四边形(平行四边形的定义).
探究新知判定定理1 (判定方法2) :
两组对边分别相等的四边形是平行四边形.在四边形ABCD中, ∵ AB=CD,AD=BC. ∴四边形ABCD是平行四边形(两组对边分别相等的四边形是平行四边形)ADBC探究新知判定定理2 (判定方法3) :已知:在四边形ABCD中,AB//CD, AB = CD. 求 证:四边形ABCD是平行四边形.一组对边平行且相等的四边形是平行四边形.证明:连接AC∴△ABC≌△CDA(SAS),∵ AB//CD,∴∠CAB=∠ACD,∠ACB= ∠ CAD,∴AB//CD,AD//BC,∴四边形ABCD是平行四边形(平行四边形的定义).
12∴∠1 = ∠2,又∵AB=CD,AC = CA, 从边出发:探究新知在四边形ABCD中, ∵ AB//CD, AB = CD. ∴ 四边形ABCD是平行四边形(一组对边平行且相等的四边形是平行四边形)判定定理2 (判定方法3) :
一组对边平行且相等的四边形是平行四边形.ADBC探究新知一组对边平行,另一组对边相等的四边形是平行四边形吗??思考假命题应举反例说明!如图,一组对边AB//CD,另一组对边AD与BC相等.
但是四边形ABCD却不是平行四边形,是等腰梯形!
思考! 如图,将两根细木条AC、BD的中心重叠,用小钉绞合在一起,用橡皮筋连接木条的顶点,做成一个四边形ABCD,转动两根木条,它一直是一个平行四边形吗?你能证明吗?你又能得到什么结论? 对角线互相平分的四边形是平行四边形.几何语言:∵OA=OC,OB=OD,
∴四边形ABCD是平行四边形.到目前判定平行四边形的方法:两组对边分别平行(定义)两组对边分别相等(判定1)一组对边平行且相等(判定2)可判定四边形
是平行四边形从边出发:归纳小结从对角线出发:两条对角线互相平分(判定3)
平行四边形.思考:∵AB∥CD且AD∥BC(已知),
∴四边形ABCD是平行四边形(平行四边形的定义).符号语言:平行四边形的判定方法1平行四边形两组对边分别平行性质!两组对边分别平行平行四边形判定! 通过前面的学习,我们知道,平行四边形的对边相等、对角相等、对角线互相平分,那么这些命题的逆命题成立吗??思考两组对边分别相等的四边形是平行四边形.已知:四边形ABCD中,AB=CD, AD=BC. 求证:四边形ABCD是平行四边形. 从边出发:判定定理1 (判定方法2):
证明:连接AC∴△ABC≌△CDA(SSS).∵ AB=CD,AD=CB,AC=CA,∴∠CAB=∠ACD,∠ACB= ∠CAD,∴AB//CD,AD//BC,∴四边形ABCD是平行四边形(平行四边形的定义).
探究新知判定定理1 (判定方法2) :
两组对边分别相等的四边形是平行四边形.在四边形ABCD中, ∵ AB=CD,AD=BC. ∴四边形ABCD是平行四边形(两组对边分别相等的四边形是平行四边形)ADBC探究新知判定定理2 (判定方法3) :已知:在四边形ABCD中,AB//CD, AB = CD. 求 证:四边形ABCD是平行四边形.一组对边平行且相等的四边形是平行四边形.证明:连接AC∴△ABC≌△CDA(SAS),∵ AB//CD,∴∠CAB=∠ACD,∠ACB= ∠ CAD,∴AB//CD,AD//BC,∴四边形ABCD是平行四边形(平行四边形的定义).
12∴∠1 = ∠2,又∵AB=CD,AC = CA, 从边出发:探究新知在四边形ABCD中, ∵ AB//CD, AB = CD. ∴ 四边形ABCD是平行四边形(一组对边平行且相等的四边形是平行四边形)判定定理2 (判定方法3) :
一组对边平行且相等的四边形是平行四边形.ADBC探究新知一组对边平行,另一组对边相等的四边形是平行四边形吗??思考假命题应举反例说明!如图,一组对边AB//CD,另一组对边AD与BC相等.
但是四边形ABCD却不是平行四边形,是等腰梯形!
思考! 如图,将两根细木条AC、BD的中心重叠,用小钉绞合在一起,用橡皮筋连接木条的顶点,做成一个四边形ABCD,转动两根木条,它一直是一个平行四边形吗?你能证明吗?你又能得到什么结论? 对角线互相平分的四边形是平行四边形.几何语言:∵OA=OC,OB=OD,
∴四边形ABCD是平行四边形.到目前判定平行四边形的方法:两组对边分别平行(定义)两组对边分别相等(判定1)一组对边平行且相等(判定2)可判定四边形
是平行四边形从边出发:归纳小结从对角线出发:两条对角线互相平分(判定3)
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
