高中数学人教A版选修1-2第一章第2节《独立性检验的基本思想及其初步应用》课件(共18张PPT)
文档属性
| 名称 | 高中数学人教A版选修1-2第一章第2节《独立性检验的基本思想及其初步应用》课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-25 13:18:11 | ||
图片预览



文档简介
(共18张PPT)
课题:独立性检验的基本思想及其初步应用
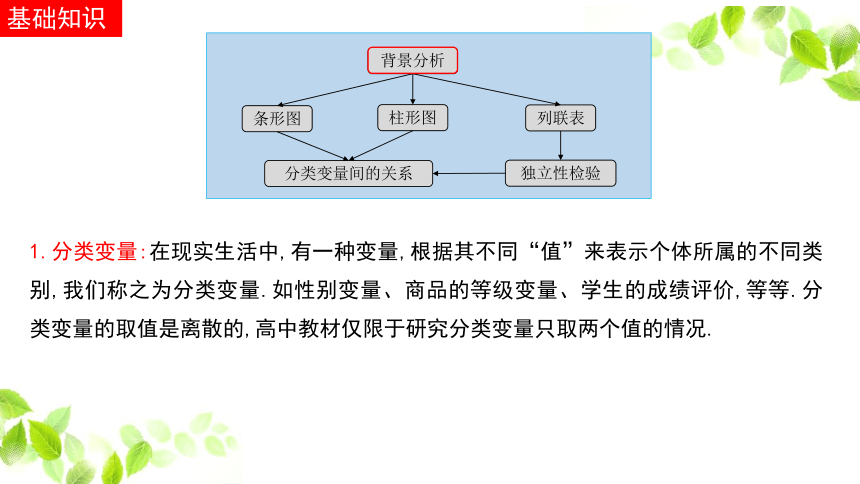
基础知识
1.分类变量:在现实生活中,有一种变量,根据其不同“值”来表示个体所属的不同类别,我们称之为分类变量.如性别变量、商品的等级变量、学生的成绩评价,等等.分类变量的取值是离散的,高中教材仅限于研究分类变量只取两个值的情况.
背景分析
条形图
柱形图
列联表
分类变量间的关系
独立性检验
背景分析
基础知识
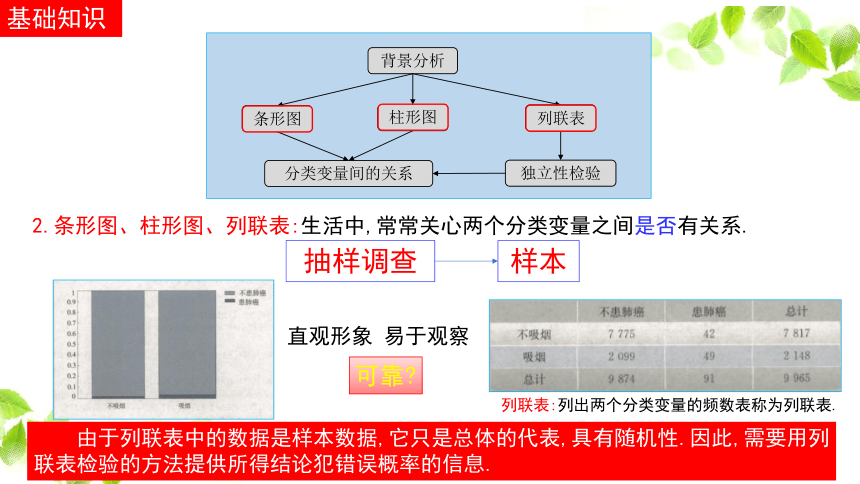
2.条形图、柱形图、列联表:生活中,常常关心两个分类变量之间是否有关系.
背景分析
条形图
柱形图
列联表
分类变量间的关系
独立性检验
样本
抽样调查
条形图
柱形图
列联表
直观形象 易于观察
列联表:列出两个分类变量的频数表称为列联表.
可靠?
由于列联表中的数据是样本数据,它只是总体的代表,具有随机性.因此,需要用列联表检验的方法提供所得结论犯错误概率的信息.
基础知识
背景分析
条形图
柱形图
列联表
分类变量间的关系
独立性检验
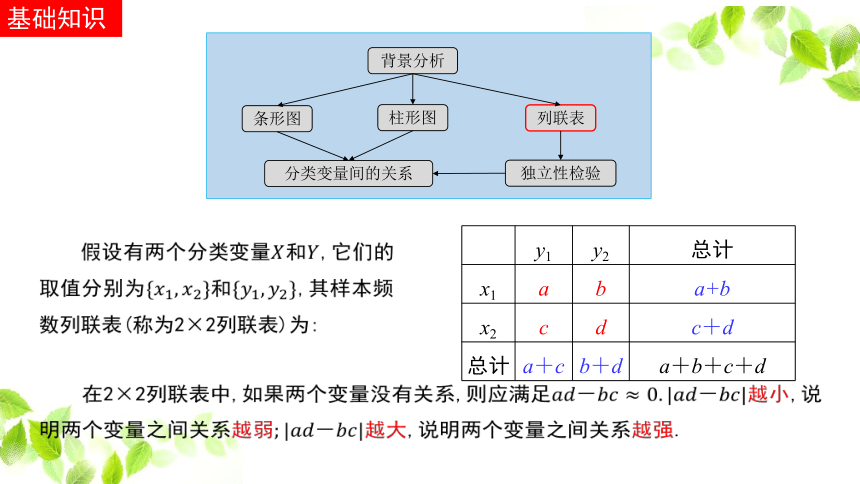
假设有两个分类变量和,它们的取值分别为和,其样本频数列联表(称为2×2列联表)为:
? y1 y2 总计
x1 a b a+b
x2 c d c+d
总计 a+c b+d a+b+c+d
在2×2列联表中,如果两个变量没有关系,则应满足越小,说明两个变量之间关系越弱越大,说明两个变量之间关系越强.
基础知识
背景分析
条形图
柱形图
列联表
分类变量间的关系
独立性检验
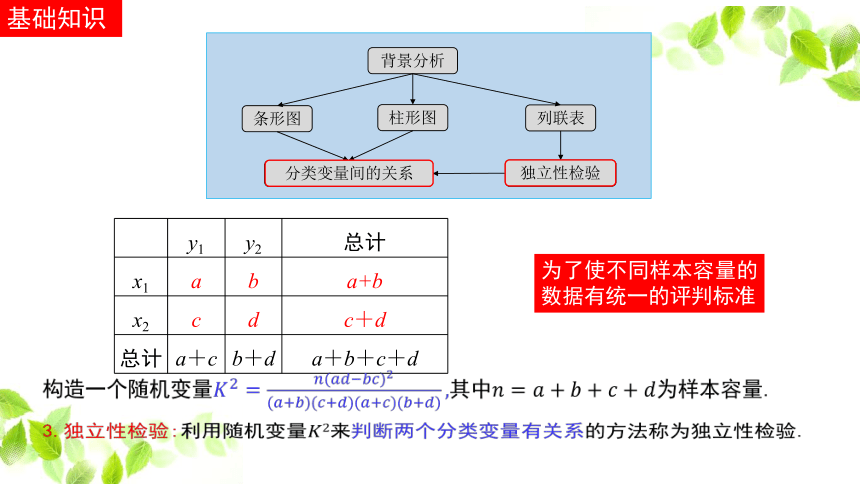
? y1 y2 总计
x1 a b a+b
x2 c d c+d
总计 a+c b+d a+b+c+d
独立性检验
构造一个随机变量其中为样本容量.
3.独立性检验:利用随机变量来判断两个分类变量有关系的方法称为独立性检验.
为了使不同样本容量的数据有统一的评判标准
分类变量间的关系
基础知识
(2)根据实际问题确定容许推断“有关系”犯错误概率的上界,查表确定临界值(意指当,就认为“有关系”;否则就认为“没有关系”.这样的就称为一个判断规则的临界值);
(1)根据公式,计算随机变量的观测值
4.独立性检验的具体做法:
假设:两个分类变量没有关系.
(3)如果,就推断“有关系”.这种推断犯错误的概率不超过;否则,就认为在犯错误的概率不超过的前提下不能推断“有关系”.
讲练结合
例1(1).为调查中学生近视情况,测得某校男生150名中有80名近视,在140名女生中有70名近视.在检验这些学生眼睛近视是否与性别有关时,用下列哪种方法最有说服力( ).
回归分析 均值与方差
独立性检验 概率
解析:“近视”与“性别”是两类变量,其是否有关,应用独立性检验判断.
例1(2).为了调查用电脑时间与视力下降是否有关系,现从某小区中抽取100位居民进行调查.经过计算得,那么有___%的把握认为用电脑时间与视力下降有关系.
解析:根据表格发现,所以根据独立性检验原理可知有的把握认为用电脑时间与视力下降有关系.
95
0.05 0.025 0.010 0.005 0.001
3.841 5.024 6.635 7.879 10.828
讲练结合
练习:为了判断高三年级学生是否选修文科与性别的关系,现随机抽取50名学生,得到如下2×2列联表:
? 理科 文科
男 13 10
女 7 20
已知.根据表中数据,得到的观测值.则认为选修文科与性别有关系出错的可能性为____.
解析:的观测值,这表明小概率事件发生.根据独立性检验的基本原理,应该断定“是否选修文科与性别之间有关系”成立,并且这种判断出错的可能性约为.
讲练结合
例2.有甲、乙两个班级进行数学考试,按照大于等于85分为优秀,85分以下为非优秀统计成绩,得到如下列联表:
? 优秀 非优秀 总计
甲班 10 ?
乙班 30 ?
合计 ? ? ?
0.05 0.025 0.010 0.005
3.841 5.024 6.635 7.879
讲练结合
已知在全部105人中随机抽取1人,成绩优秀的概率为,则下列说法正确的是( )
.列联表中的值为30,的值为35
.列联表中的值为15,的值为50
.根据列联表中的数据,若按97.5%的可靠性要求,能认为“成绩与班级有关系”
.根据列联表中的数据,若按97.5%的可靠性要求,不能认为“成绩与班级有关系”
20
45
5.024
30
50
105
55
75
练习:某商场为提高服务质量,随机调查了50名男顾客和50名女顾客,每位顾客对该商场的服务给出满意或不满意的评价,得到下面列联表:
? 满意 不满意 总计
男顾客 ?40 10? 50
女顾客 ?30 20? 50
总计 70 30 100
能否有的把握认为男、女顾客对该商场服务的评价有差异?
附
0.050 0.010 0.001
3.841 6.635 10.828
解析:由题意
故有的把握认为男、女顾客对该商场服务的评价有差异.
讲练结合
例3.某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率,选取40名工人,随机分成两组,每组20人,第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位:min)绘制了如图所示的茎叶图:
(1)根据茎叶图判断哪种生产方式的效率更高?并说明理由;
第二种生产方式的效率更高.
解析:(1)第一种生产方式时间集中在区间,且平均工作时间
第二种生产方式的时间集中在区间,且平均工作时间
所以第一种生产方式完成任务的平均时间大于第二种.
讲练结合
例3.某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率,选取40名工人,随机分成两组,每组20人,第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位:min)绘制了如图所示的茎叶图:
(2)求40名工人完成生产任务所需时间的中位数,并将完成生产任务所需时间超过和不超过的工人数填入下面的列联表:
? 超过 不超过 总计
第一种生产方式 ? ?
第二种生产方式 ? ?
总计
解析:(2)由茎叶图数据得到.由此填写列联表.
15 5 20
5 15 20
20 20 40
讲练结合
例3.某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率,选取40名工人,随机分成两组,每组20人,第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位:min)绘制了如图所示的茎叶图:
0.050 0.010 0.001
3.841 6.635 10.828
(3)根据(2)中的列联表,能否有99%的把握认为两种生产方式的效率有差异?
附:
? 超过 不超过 总计
第一种生产方式 ? ?
第二种生产方式 ? ?
总计
15 5 20
5 15 20
20 20 40
解析:(3)
所以有的把握认为两种生产方式的效率有差异.
讲练结合
讲练结合
附:
讲练结合
解析:(1)从高一年级学生中随机抽取1人,抽出男生的概率约为;
(2)根据统计数据,可得列联表如下:
则的观测值为
所以能在犯错误的概率不超过的前提下认为科类的选择与性别有关.
本课小结
背景分析
条形图
柱形图
列联表
分类变量间的关系
独立性检验
两个分类变量独立性检验的基本思想:
在假设“两个分类变量没有关系”的前提下,构造一个有利于“两个分类变量有关系”的小概率事件(即概率不超过的事件).如果样本观测数据使得这个小概率事件发生,就可以在犯错误的概率不超过的前提下认为“两个分类变量有关系”.
独立性检验的步骤:
(1)通过样本数据做出列联表;
(2)根据公式计算观测值;
(3)通过临界值表得出“两个分类变量是否有关系”的结论.
感 谢 收 看
课题:独立性检验的基本思想及其初步应用
基础知识
1.分类变量:在现实生活中,有一种变量,根据其不同“值”来表示个体所属的不同类别,我们称之为分类变量.如性别变量、商品的等级变量、学生的成绩评价,等等.分类变量的取值是离散的,高中教材仅限于研究分类变量只取两个值的情况.
背景分析
条形图
柱形图
列联表
分类变量间的关系
独立性检验
背景分析
基础知识
2.条形图、柱形图、列联表:生活中,常常关心两个分类变量之间是否有关系.
背景分析
条形图
柱形图
列联表
分类变量间的关系
独立性检验
样本
抽样调查
条形图
柱形图
列联表
直观形象 易于观察
列联表:列出两个分类变量的频数表称为列联表.
可靠?
由于列联表中的数据是样本数据,它只是总体的代表,具有随机性.因此,需要用列联表检验的方法提供所得结论犯错误概率的信息.
基础知识
背景分析
条形图
柱形图
列联表
分类变量间的关系
独立性检验
假设有两个分类变量和,它们的取值分别为和,其样本频数列联表(称为2×2列联表)为:
? y1 y2 总计
x1 a b a+b
x2 c d c+d
总计 a+c b+d a+b+c+d
在2×2列联表中,如果两个变量没有关系,则应满足越小,说明两个变量之间关系越弱越大,说明两个变量之间关系越强.
基础知识
背景分析
条形图
柱形图
列联表
分类变量间的关系
独立性检验
? y1 y2 总计
x1 a b a+b
x2 c d c+d
总计 a+c b+d a+b+c+d
独立性检验
构造一个随机变量其中为样本容量.
3.独立性检验:利用随机变量来判断两个分类变量有关系的方法称为独立性检验.
为了使不同样本容量的数据有统一的评判标准
分类变量间的关系
基础知识
(2)根据实际问题确定容许推断“有关系”犯错误概率的上界,查表确定临界值(意指当,就认为“有关系”;否则就认为“没有关系”.这样的就称为一个判断规则的临界值);
(1)根据公式,计算随机变量的观测值
4.独立性检验的具体做法:
假设:两个分类变量没有关系.
(3)如果,就推断“有关系”.这种推断犯错误的概率不超过;否则,就认为在犯错误的概率不超过的前提下不能推断“有关系”.
讲练结合
例1(1).为调查中学生近视情况,测得某校男生150名中有80名近视,在140名女生中有70名近视.在检验这些学生眼睛近视是否与性别有关时,用下列哪种方法最有说服力( ).
回归分析 均值与方差
独立性检验 概率
解析:“近视”与“性别”是两类变量,其是否有关,应用独立性检验判断.
例1(2).为了调查用电脑时间与视力下降是否有关系,现从某小区中抽取100位居民进行调查.经过计算得,那么有___%的把握认为用电脑时间与视力下降有关系.
解析:根据表格发现,所以根据独立性检验原理可知有的把握认为用电脑时间与视力下降有关系.
95
0.05 0.025 0.010 0.005 0.001
3.841 5.024 6.635 7.879 10.828
讲练结合
练习:为了判断高三年级学生是否选修文科与性别的关系,现随机抽取50名学生,得到如下2×2列联表:
? 理科 文科
男 13 10
女 7 20
已知.根据表中数据,得到的观测值.则认为选修文科与性别有关系出错的可能性为____.
解析:的观测值,这表明小概率事件发生.根据独立性检验的基本原理,应该断定“是否选修文科与性别之间有关系”成立,并且这种判断出错的可能性约为.
讲练结合
例2.有甲、乙两个班级进行数学考试,按照大于等于85分为优秀,85分以下为非优秀统计成绩,得到如下列联表:
? 优秀 非优秀 总计
甲班 10 ?
乙班 30 ?
合计 ? ? ?
0.05 0.025 0.010 0.005
3.841 5.024 6.635 7.879
讲练结合
已知在全部105人中随机抽取1人,成绩优秀的概率为,则下列说法正确的是( )
.列联表中的值为30,的值为35
.列联表中的值为15,的值为50
.根据列联表中的数据,若按97.5%的可靠性要求,能认为“成绩与班级有关系”
.根据列联表中的数据,若按97.5%的可靠性要求,不能认为“成绩与班级有关系”
20
45
5.024
30
50
105
55
75
练习:某商场为提高服务质量,随机调查了50名男顾客和50名女顾客,每位顾客对该商场的服务给出满意或不满意的评价,得到下面列联表:
? 满意 不满意 总计
男顾客 ?40 10? 50
女顾客 ?30 20? 50
总计 70 30 100
能否有的把握认为男、女顾客对该商场服务的评价有差异?
附
0.050 0.010 0.001
3.841 6.635 10.828
解析:由题意
故有的把握认为男、女顾客对该商场服务的评价有差异.
讲练结合
例3.某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率,选取40名工人,随机分成两组,每组20人,第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位:min)绘制了如图所示的茎叶图:
(1)根据茎叶图判断哪种生产方式的效率更高?并说明理由;
第二种生产方式的效率更高.
解析:(1)第一种生产方式时间集中在区间,且平均工作时间
第二种生产方式的时间集中在区间,且平均工作时间
所以第一种生产方式完成任务的平均时间大于第二种.
讲练结合
例3.某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率,选取40名工人,随机分成两组,每组20人,第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位:min)绘制了如图所示的茎叶图:
(2)求40名工人完成生产任务所需时间的中位数,并将完成生产任务所需时间超过和不超过的工人数填入下面的列联表:
? 超过 不超过 总计
第一种生产方式 ? ?
第二种生产方式 ? ?
总计
解析:(2)由茎叶图数据得到.由此填写列联表.
15 5 20
5 15 20
20 20 40
讲练结合
例3.某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率,选取40名工人,随机分成两组,每组20人,第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位:min)绘制了如图所示的茎叶图:
0.050 0.010 0.001
3.841 6.635 10.828
(3)根据(2)中的列联表,能否有99%的把握认为两种生产方式的效率有差异?
附:
? 超过 不超过 总计
第一种生产方式 ? ?
第二种生产方式 ? ?
总计
15 5 20
5 15 20
20 20 40
解析:(3)
所以有的把握认为两种生产方式的效率有差异.
讲练结合
讲练结合
附:
讲练结合
解析:(1)从高一年级学生中随机抽取1人,抽出男生的概率约为;
(2)根据统计数据,可得列联表如下:
则的观测值为
所以能在犯错误的概率不超过的前提下认为科类的选择与性别有关.
本课小结
背景分析
条形图
柱形图
列联表
分类变量间的关系
独立性检验
两个分类变量独立性检验的基本思想:
在假设“两个分类变量没有关系”的前提下,构造一个有利于“两个分类变量有关系”的小概率事件(即概率不超过的事件).如果样本观测数据使得这个小概率事件发生,就可以在犯错误的概率不超过的前提下认为“两个分类变量有关系”.
独立性检验的步骤:
(1)通过样本数据做出列联表;
(2)根据公式计算观测值;
(3)通过临界值表得出“两个分类变量是否有关系”的结论.
感 谢 收 看
