人教版七年级数学下册 6.3实数 课件(27张)
文档属性
| 名称 | 人教版七年级数学下册 6.3实数 课件(27张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-21 21:16:41 | ||
图片预览






文档简介
(共27张PPT)
实
数
有理数
整数
分数
有理数包括哪些数?
3 = 3.0,
★任何一个有理数都可以写成有限小数或无限循环小数的形式.
探究
反过来,任何有限小数或无限循环小数也都是有理数
=
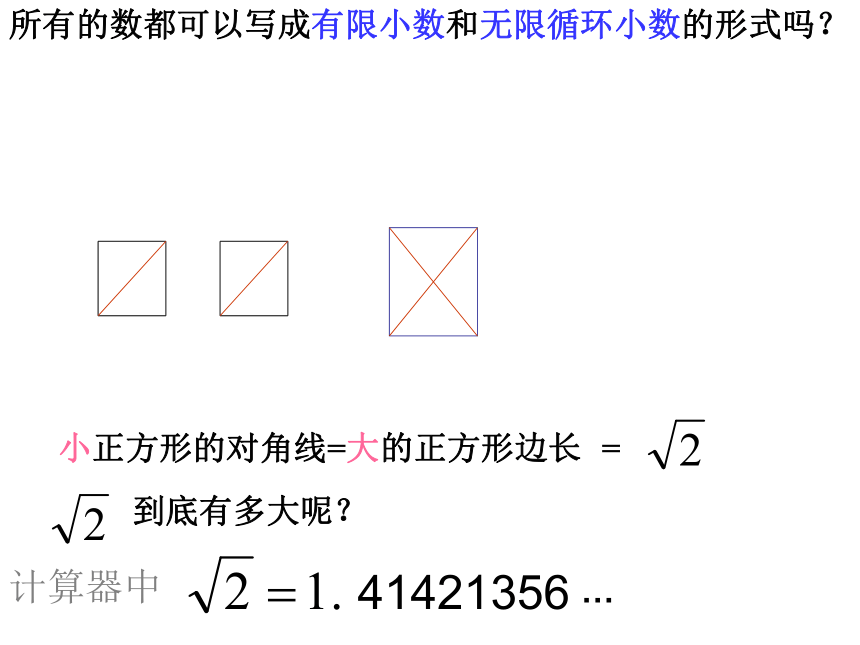
小正方形的对角线=大的正方形边长
所有的数都可以写成有限小数和无限循环小数的形式吗?
到底有多大呢?
计算器中
41421356
…
的数值
1.41421356237309504880168872420969807856967187537694807317667973799073247846210703885038753432764157273501384623091229702492483605585073721264412149709993583141322266592750559275579995050115278206057147010955997160597027453459686201472851741864088919860955232923048430871432145083976260362799525140798968725339654633180882964062061525835239505474575028775996172983557522033753185701135437460340849884716038689997069900481503054402779031645424782306849293691862158057846311159666871301301561856898723723528850926486124949771542183342042856860601468247207714358548741556570696776537202264854470158588016207584749226572260020855844665214583988939443709265918003113882464681570826301005948587040031864803421948972782906410450726368813137398552561173220402450912277002269411275736272804957381089675040183698683684507257993647290607629969413804756548237289971803268024744206292691248…
无限不循环的小数 ---- 叫做无理数.
(1) 你能举出一些无理数吗?
无理数是广泛存在的:
= 1.732050807568877293527…
π=3.141592653589793238…
0.101001000…(两个1之间依次多一个0)
至2002年底,科学家们用超级计算机已把π的值算到小数点后12411亿位.
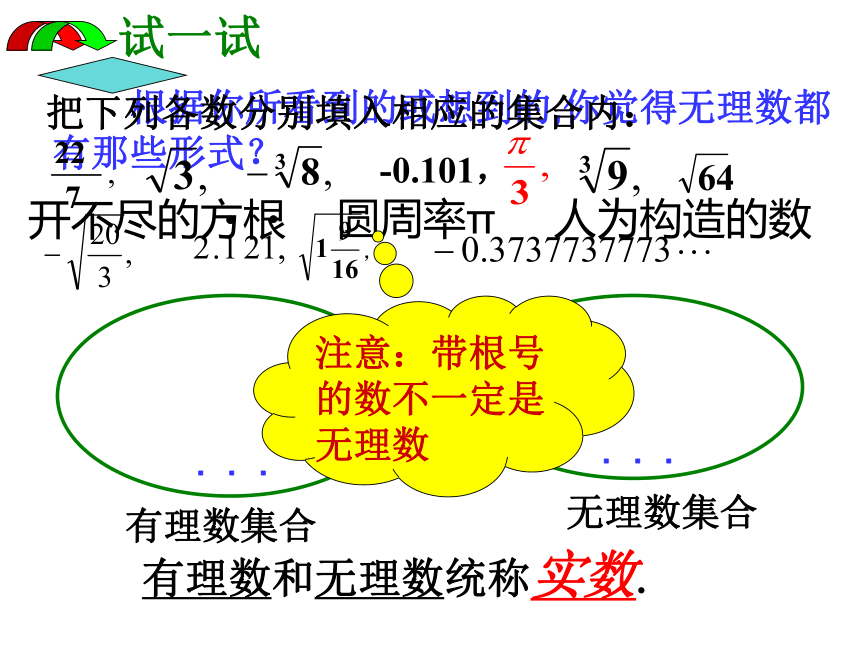
根据你所看到的或想到的,你觉得无理数都有那些形式?
把下列各数分别填入相应的集合内:
-0.101,
有理数集合
无理数集合
有理数和无理数统称实数.
圆周率π
开不尽的方根
人为构造的数
注意:带根号的数不一定是无理数
无理数和有理数一样,也有正负之分。
正
负
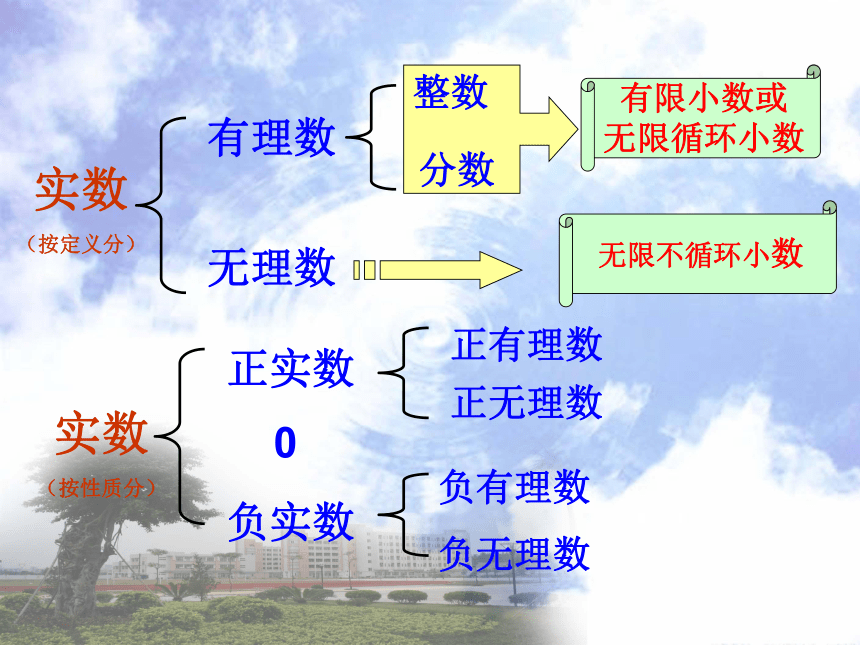
有理数
无理数
分数
整数
有限小数或
无限循环小数
无限不循环小数
实数
(按定义分)
把下列各数填入相应的集合内:
(1)有理数集合:
(2)无理数集合:
(4)负实数集合:
3.1415926,
( 3 )正实数集合:
(5)实数集合:
1.实数不是有理数就是无理数。( )
2.无理数都是无限不循环小数。( )
4.无理数都是无限小数。( )
3.带根号的数都是无理数。( )
5.无理数一定都带根号。( )
×
×
D
如图,直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上一点从原点到达A点,则点A的坐标为多少?
A
问题1.无理数能在数轴上表示出来吗?
每一个实数都可以用数轴上的一个点来表示;
反过来,数轴上的每一点都表示一个实数。
★实数和数轴上的点是一一对应的.
随堂练习:
解:点A表示-1.5;
点D表示3;
6.用教材中的计算器依次按键如下,显示的结果在数轴上对应点的位置介于( )
A.B与C之间 B.C与D之间
C.E与F之间 D.A与B之间
7.(2017·北京)写出一个比-4大且比-3小的无理数:____.
A
-π
13.若数轴上的A,B,C三点表示的实数分别为a,1,-1,则|a+1|表示( )
A.A,B两点间的距离
B.A,C两点间的距离
C.A,B两点到原点的距离之和
D.A,C两点到原点的距离之和
B
在实数范围内,相反数、倒数、绝对值的意义和有理数范围内的相反数、倒数、绝对值的意义完全一样。
你能解答下列问题吗?
(1) 的相反数是 ,
的相反数是 ,
0 的相反数是 ;
(2) = , = ,
= .
2.探究新知
练习:
P56 第3题
结合有理数相反数和绝对值的意义,
你能说说实数关于相反数和绝对值的意义吗?
2.探究新知
数 的相反数是 ,
一个正实数的绝对
值是它本身;
一个负实数的绝对
值是它的相反数;
0的绝对值是0.
填空
1、正实数的绝对值是 ,0的绝对值是 ,负实数的绝对值是 .
它本身
0
它的相反数
例1:
(1)分别写出- , 的相反数;
(2)求
(3)已知一个数的绝对值是 ,
求这个数.
把下列各数分别填入相应的集合内:
有理数集合
无理数集合
一、判断下列说法是否正确:
1.实数不是有理数就是无理数. ( )
2.无限小数都是无理数. ( )
3.无理数都是无限小数. ( )
4.带根号的数都是无理数. ( )
5.两个无理数之和一定是无理数.( )
6.所有的有理数都可以在数轴上表示,反过来,数轴上所有的点都表示有理数. ( )
作业:
课本P57 2,3,5
实
数
有理数
整数
分数
有理数包括哪些数?
3 = 3.0,
★任何一个有理数都可以写成有限小数或无限循环小数的形式.
探究
反过来,任何有限小数或无限循环小数也都是有理数
=
小正方形的对角线=大的正方形边长
所有的数都可以写成有限小数和无限循环小数的形式吗?
到底有多大呢?
计算器中
41421356
…
的数值
1.41421356237309504880168872420969807856967187537694807317667973799073247846210703885038753432764157273501384623091229702492483605585073721264412149709993583141322266592750559275579995050115278206057147010955997160597027453459686201472851741864088919860955232923048430871432145083976260362799525140798968725339654633180882964062061525835239505474575028775996172983557522033753185701135437460340849884716038689997069900481503054402779031645424782306849293691862158057846311159666871301301561856898723723528850926486124949771542183342042856860601468247207714358548741556570696776537202264854470158588016207584749226572260020855844665214583988939443709265918003113882464681570826301005948587040031864803421948972782906410450726368813137398552561173220402450912277002269411275736272804957381089675040183698683684507257993647290607629969413804756548237289971803268024744206292691248…
无限不循环的小数 ---- 叫做无理数.
(1) 你能举出一些无理数吗?
无理数是广泛存在的:
= 1.732050807568877293527…
π=3.141592653589793238…
0.101001000…(两个1之间依次多一个0)
至2002年底,科学家们用超级计算机已把π的值算到小数点后12411亿位.
根据你所看到的或想到的,你觉得无理数都有那些形式?
把下列各数分别填入相应的集合内:
-0.101,
有理数集合
无理数集合
有理数和无理数统称实数.
圆周率π
开不尽的方根
人为构造的数
注意:带根号的数不一定是无理数
无理数和有理数一样,也有正负之分。
正
负
有理数
无理数
分数
整数
有限小数或
无限循环小数
无限不循环小数
实数
(按定义分)
把下列各数填入相应的集合内:
(1)有理数集合:
(2)无理数集合:
(4)负实数集合:
3.1415926,
( 3 )正实数集合:
(5)实数集合:
1.实数不是有理数就是无理数。( )
2.无理数都是无限不循环小数。( )
4.无理数都是无限小数。( )
3.带根号的数都是无理数。( )
5.无理数一定都带根号。( )
×
×
D
如图,直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上一点从原点到达A点,则点A的坐标为多少?
A
问题1.无理数能在数轴上表示出来吗?
每一个实数都可以用数轴上的一个点来表示;
反过来,数轴上的每一点都表示一个实数。
★实数和数轴上的点是一一对应的.
随堂练习:
解:点A表示-1.5;
点D表示3;
6.用教材中的计算器依次按键如下,显示的结果在数轴上对应点的位置介于( )
A.B与C之间 B.C与D之间
C.E与F之间 D.A与B之间
7.(2017·北京)写出一个比-4大且比-3小的无理数:____.
A
-π
13.若数轴上的A,B,C三点表示的实数分别为a,1,-1,则|a+1|表示( )
A.A,B两点间的距离
B.A,C两点间的距离
C.A,B两点到原点的距离之和
D.A,C两点到原点的距离之和
B
在实数范围内,相反数、倒数、绝对值的意义和有理数范围内的相反数、倒数、绝对值的意义完全一样。
你能解答下列问题吗?
(1) 的相反数是 ,
的相反数是 ,
0 的相反数是 ;
(2) = , = ,
= .
2.探究新知
练习:
P56 第3题
结合有理数相反数和绝对值的意义,
你能说说实数关于相反数和绝对值的意义吗?
2.探究新知
数 的相反数是 ,
一个正实数的绝对
值是它本身;
一个负实数的绝对
值是它的相反数;
0的绝对值是0.
填空
1、正实数的绝对值是 ,0的绝对值是 ,负实数的绝对值是 .
它本身
0
它的相反数
例1:
(1)分别写出- , 的相反数;
(2)求
(3)已知一个数的绝对值是 ,
求这个数.
把下列各数分别填入相应的集合内:
有理数集合
无理数集合
一、判断下列说法是否正确:
1.实数不是有理数就是无理数. ( )
2.无限小数都是无理数. ( )
3.无理数都是无限小数. ( )
4.带根号的数都是无理数. ( )
5.两个无理数之和一定是无理数.( )
6.所有的有理数都可以在数轴上表示,反过来,数轴上所有的点都表示有理数. ( )
作业:
课本P57 2,3,5
