2019-2020学年人教版七年级数学下册 5.1 相交线 同步测试(解析版)
文档属性
| 名称 | 2019-2020学年人教版七年级数学下册 5.1 相交线 同步测试(解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 218.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-21 00:00:00 | ||
图片预览



文档简介
2019-2020学年人教版七年级数学下册 5.1 相交线 同步测试
一.选择题(共10小题)
1.下列说法中正确的个数是( )
①过两点有且只有一条直线; ②两直线相交只有一个交点;
③0的绝对值是它本身 ④射线AB和射线BA是同一条射线.
A.1个 B.2个 C.3个 D.4个
2.下列说法不正确的是( )
A.对顶角相等
B.两点确定一条直线
C.一个角的补角一定大于这个角
D.两点之间线段最短
3.如图,从位置P到直线公路MN有四条小道,其中路程最短的是( )
A.PA B.PB C.PC D.PD
4.如图,∠1与∠2是同位角的个数有( )
A.1个 B.2个 C.3个 D.4个
5.在平面内,过一点画已知直线的垂线,可画垂线的条数是( )
A.0 B.1 C.2 D.无数
6.如图,下列结论中错误的是( )
A.∠1与∠2是同旁内角 B.∠1与∠6是内错角
C.∠2与∠5是内错角 D.∠3与∠5是同位角
7.如图所示,下列结论中不正确的是( )
A.∠1和∠2是同位角 B.∠2和∠3是同旁内角
C.∠1和∠4是同位角 D.∠2和∠4是内错角
8.下列各图中,∠1=∠2一定成立的是( )
A. B.
C. D.
9.如图,∠ACB=90°,CD⊥AB,垂足为D,则下面结论中正确的有:( )
①AC与BC互相垂直;
②CD与AC互相垂直;
③点A到BC的垂线段是BC;
④点C到AB的距离是CD;
⑤线段BC的长度是点B到AC的距离;
⑥线段BC是点B到AC的距离
A.2个 B.3个 C.4个 D.5个
10.下列图形中,∠1与∠2是同位角的是( )
A. B.
C. D.
二.填空题(共8小题)
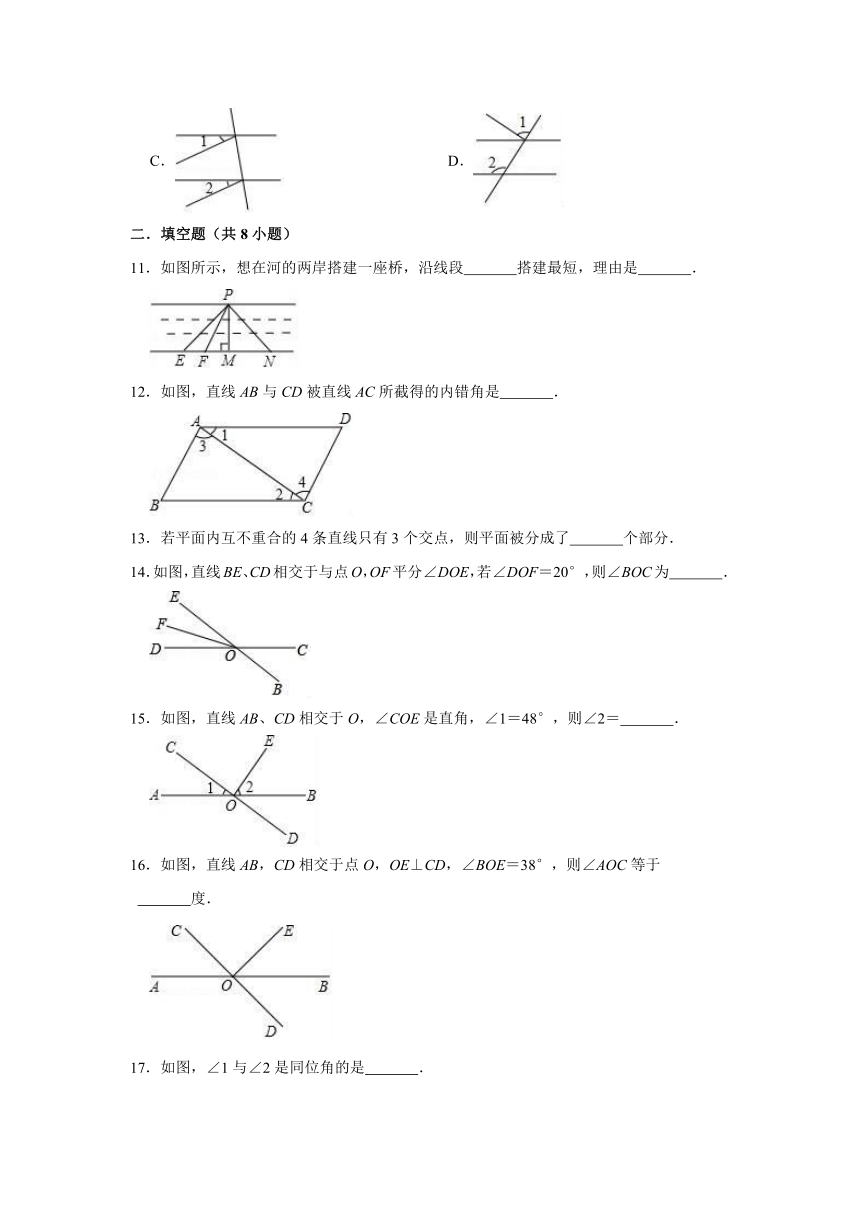
11.如图所示,想在河的两岸搭建一座桥,沿线段 搭建最短,理由是 .
12.如图,直线AB与CD被直线AC所截得的内错角是 .
13.若平面内互不重合的4条直线只有3个交点,则平面被分成了 个部分.
14.如图,直线BE、CD相交于与点O,OF平分∠DOE,若∠DOF=20°,则∠BOC为 .
15.如图,直线AB、CD相交于O,∠COE是直角,∠1=48°,则∠2= .
16.如图,直线AB,CD相交于点O,OE⊥CD,∠BOE=38°,则∠AOC等于
度.
17.如图,∠1与∠2是同位角的是 .
18.如图,BC⊥AC,BC=12,AC=9,AB=15,则点C到线段AB的距离是 .
三.解答题(共7小题)
19.如图,A、B、C是平面内三点.
(1)按要求作图:
①作射线BC,过点B作直线l,使A、C两点在直线l两旁;
②点P为直线l上任意一点,点Q为直线BC上任意一点,连结线段AP、PQ;
(2)在(1)所作图形中,若点A到直线l的距离为2,点A到直线BC的距离为5,点A、B
之间的距离为8,点A、C之间的距离为6,则AP+PQ的最小值为 ,依据是 .
20.如图,直线AB和CD交于点O,∠COF=90°,OC平分∠AOE,∠COE=40°.
(1)求∠BOD的度数;
(2)OF平分∠BOE吗?请说明理由.
21.已知:直线AB与直线CD相交于点O,∠BOC=45°,
(1)如图1,若EO⊥AB,求∠DOE的度数;
(2)如图2,若EO平分∠AOC,求∠DOE的度数.
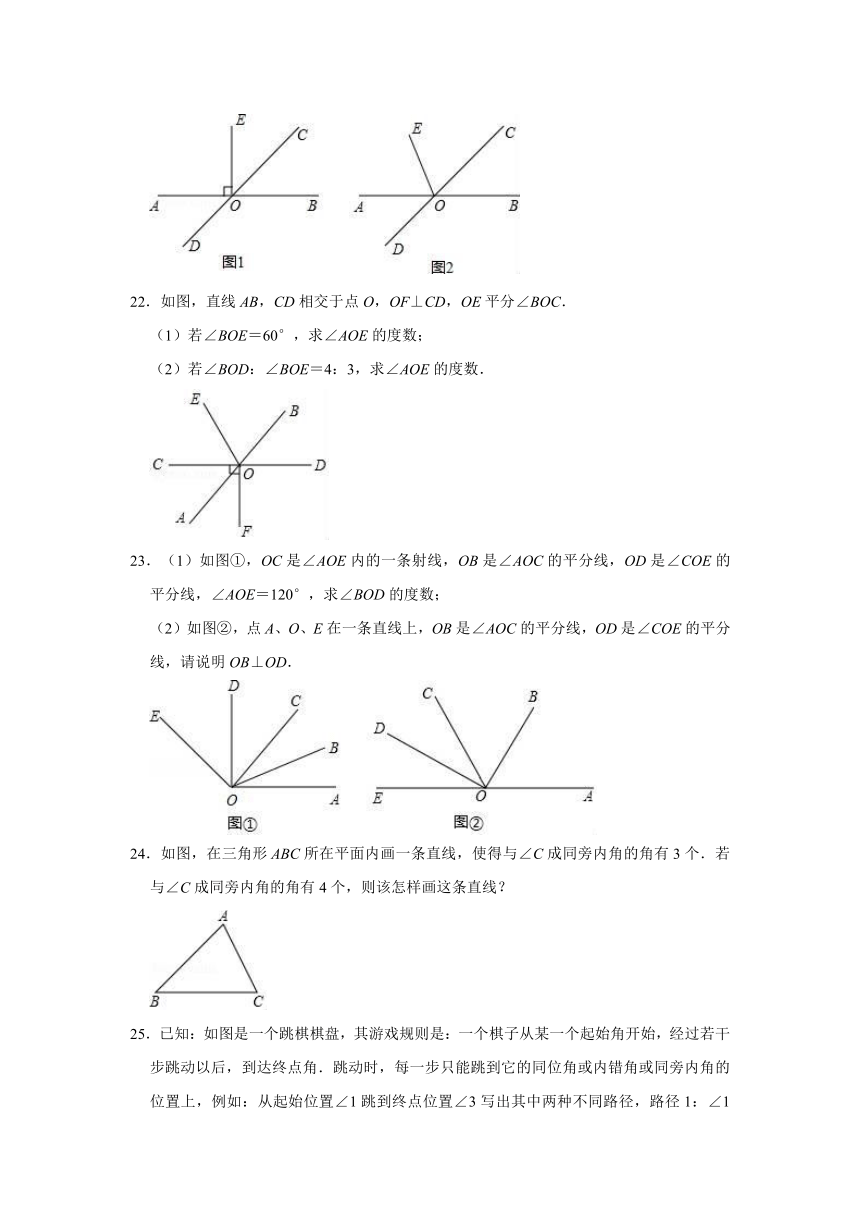
22.如图,直线AB,CD相交于点O,OF⊥CD,OE平分∠BOC.
(1)若∠BOE=60°,求∠AOE的度数;
(2)若∠BOD:∠BOE=4:3,求∠AOE的度数.
23.(1)如图①,OC是∠AOE内的一条射线,OB是∠AOC的平分线,OD是∠COE的平分线,∠AOE=120°,求∠BOD的度数;
(2)如图②,点A、O、E在一条直线上,OB是∠AOC的平分线,OD是∠COE的平分线,请说明OB⊥OD.
24.如图,在三角形ABC所在平面内画一条直线,使得与∠C成同旁内角的角有3个.若与∠C成同旁内角的角有4个,则该怎样画这条直线?
25.已知:如图是一个跳棋棋盘,其游戏规则是:一个棋子从某一个起始角开始,经过若干步跳动以后,到达终点角.跳动时,每一步只能跳到它的同位角或内错角或同旁内角的位置上,例如:从起始位置∠1跳到终点位置∠3写出其中两种不同路径,路径1:∠1﹣同旁内角→∠9﹣内错角→∠3.
路径2:∠1一内错角→∠12一内错角→∠6﹣同位角→∠10﹣同旁内角→∠3.
试一试:(1)从起始∠1跳到终点角∠8;
(2)从起始角∠1依次按同位角、内错角、同旁内角的顺序跳,能否跳到终点∠8?
参考答案与试题解析
一.选择题(共10小题)
1.解:①过两点有且只有一条直线,故①正确;
②两直线相交只有一个交点,故②正确;
③0的绝对值是它本身,故③正确;
④射线AB和射线BA的端点不同,延伸方向也不同,不是同一条射线,故④错误.
故选:C.
2.解:A.对顶角相等,说法正确;
B.两点确定一条直线,说法正确;
C.一个角的补角不一定大于这个角,比如∠A=150°,∠A的补角为30°,但是30°<150°,故原说法错误;
D.两点之间线段最短,说法正确.
故选:C.
3.解:根据垂线段最短得,能最快到达公路MN的小道是PB,
故选:B.
4.解:这四个图中,∠1与∠2有一条边在同一条直线上,另一条边在被截线的同一方,是同位角.
故选:D.
5.解:在平面内,过一点画已知直线的垂线,可画垂线的条数是1.
故选:B.
6.解:A、∠1与∠2是同旁内角,正确,不合题意;
B、∠1与∠6是内错角,正确,不合题意;
C、∠2与∠5是内错角,错误,符合题意;
D、∠3与∠5是同位角,正确,不合题意;
故选:C.
7.解:A、∠1和∠2是同旁内角,故本选项错误,符合题意;
B、∠2和∠3是同旁内角,故本选项正确,不符合题意;
C、∠1和∠4是同位角,故本选项正确,不符合题意;
D、∠3和∠4是邻补角,故本选项正确,不符合题意;
故选:A.
8.解:根据对顶角相等可知,C选项是正确的,
故选:C.
9.解:∵∠ACB=90°,CD⊥AB,垂足为D,
∴①AC与BC互相垂直,故①正确;
②CD与AB互相垂直,与AC不垂直,故②错误;
③点A到BC的垂线段是AC,故③错误;
④点C到AB的距离是CD的长,故④错误;
⑤线段BC的长度是点B到AC的距离,故⑤正确;
⑥线段BC的长是点B到AC的距离,故⑥错误;
故选:A.
10.解:根据同位角的定义可知D选项中∠1与∠2在直线的同侧,并且在第三条直线(截线)的同旁,故是同位角.
故选:D.
二.填空题(共8小题)
11.解:∵PM⊥MN,
∴由垂线段最短可知PM是最短的,
故答案为:PM,垂线段最短.
12.解:如图所示,直线AB与CD被直线AC所截得的内错角是∠3和∠4.
故答案是:∠3和∠4.
13.解:如图,
或
所以,平面内互不重合的4条直线只有3个交点,则平面被分成了 8或9个部分.
故答案是:8或9.
14.解:∵OF平分∠DOE,若∠DOF=20°,
∴∠DOE=2∠DOF=40°,
∴∠BOC=∠DOE=40°,
故答案为:40°.
15.解:∵∠COE是直角,∠1=48°,
∴∠2=180°﹣∠COE﹣∠1=180°﹣90°﹣48°=42°.
故答案为:42°.
16.解:∵OE⊥CD,
∴∠DOE=90°,
又∵∠BOE=38°,
∴∠BOC=90°+38°=128°,
则∠AOC=180°﹣∠BOC=52°.
故答案为:52.
17.解:这四个图中,∠1与∠2有一条边在同一条直线上,另一条边在被截线的同一方,是同位角,符合的有图①②.
故答案为:①②.
18.解:∵92+122=152,
∴AC2+BC2=AB2,
∴∠C=90°,
设点C到AB的距离是h, AC?BC=AB?h,
解得:h=7.2.
故答案为:7.2.
三.解答题(共7小题)
19.解:(1)①如图1所示,射线BC,直线l即为所求;
②如图1所示,线段AP,PQ即为所求;
(2)过A作AQ⊥BC交直线l于P,
则此时,AP+PQ的值最小,
∵点A到直线BC的距离为5,
∴AP+PQ的最小值为5,
依据是垂线段最短,
故答案为:5,垂线段最短.
20.解:(1)由∠COE=40°,OC平分∠AOE,
∠AOC=40°,
∠BOD=∠AOC=40°;
(2)OF平分∠BOE,理由如下:
由∠COE=40°,∠COF=90°
得∠EOF=90°﹣40°=50°,
又∵∠BOF=∠DOF﹣∠BOD=90°﹣40°=50°,
∴∠EOF=∠BOF,
∴OF平分∠BOE.
21.解:(1)∵直线AB与直线CD相交,
∴∠AOD=∠BOC=45°.
∵EO⊥AB,
∴∠AOE=90°,
∴∠DOE=∠AOD+∠AOE=135°;
(2)∵直线AB与直线CD相交,
∴∠AOD=∠BOC=45°,∠AOC=135°,
∵EO平分∠AOC,
∴∠AOE=∠AOC=67.5°,
∴∠DOE=∠AOD+∠AOE=112.5°.
22.解:(1)∵OE平分∠BOC,∠BOE=60°,
∴∠BOC=2∠BOE=120°,
∴∠AOC=180°﹣120°=60°=∠BOD,
∴∠AOE=60°+60°=120°;
(2)∵OE平分∠BOC,
∴∠BOD:∠BOE:∠EOC=4:3:3,
∴∠BOD=180°×=72°,
∴∠BOE=180°×=54°,
∴∠AOE=72°+54°=126°.
23.解:(1)∵OB是∠AOC的平分线∴
同理,
∴∠BOD=∠BOC+∠DOC=∠AOC+∠EOC=(∠AOC+∠EOC)=∠AOE,
∵∠AOE=120°
∴
(2)由(1)可知
∵∠AOE=180°
∴
∴OB⊥OD.
24.解:如图1,与∠C成同旁内角的角分别有3个,∠CED,∠B,∠A;
如图2,与∠C成同旁内角的角分别有4个,∠CFG,∠B,∠CGF,∠A.
25.解:(1)路径∠1∠12∠8;
(2)从起始角∠1依次按同位角、内错角、同旁内角的顺序跳,能跳到终点∠8.其路径为:
路径:∠1∠10∠5∠8.
一.选择题(共10小题)
1.下列说法中正确的个数是( )
①过两点有且只有一条直线; ②两直线相交只有一个交点;
③0的绝对值是它本身 ④射线AB和射线BA是同一条射线.
A.1个 B.2个 C.3个 D.4个
2.下列说法不正确的是( )
A.对顶角相等
B.两点确定一条直线
C.一个角的补角一定大于这个角
D.两点之间线段最短
3.如图,从位置P到直线公路MN有四条小道,其中路程最短的是( )
A.PA B.PB C.PC D.PD
4.如图,∠1与∠2是同位角的个数有( )
A.1个 B.2个 C.3个 D.4个
5.在平面内,过一点画已知直线的垂线,可画垂线的条数是( )
A.0 B.1 C.2 D.无数
6.如图,下列结论中错误的是( )
A.∠1与∠2是同旁内角 B.∠1与∠6是内错角
C.∠2与∠5是内错角 D.∠3与∠5是同位角
7.如图所示,下列结论中不正确的是( )
A.∠1和∠2是同位角 B.∠2和∠3是同旁内角
C.∠1和∠4是同位角 D.∠2和∠4是内错角
8.下列各图中,∠1=∠2一定成立的是( )
A. B.
C. D.
9.如图,∠ACB=90°,CD⊥AB,垂足为D,则下面结论中正确的有:( )
①AC与BC互相垂直;
②CD与AC互相垂直;
③点A到BC的垂线段是BC;
④点C到AB的距离是CD;
⑤线段BC的长度是点B到AC的距离;
⑥线段BC是点B到AC的距离
A.2个 B.3个 C.4个 D.5个
10.下列图形中,∠1与∠2是同位角的是( )
A. B.
C. D.
二.填空题(共8小题)
11.如图所示,想在河的两岸搭建一座桥,沿线段 搭建最短,理由是 .
12.如图,直线AB与CD被直线AC所截得的内错角是 .
13.若平面内互不重合的4条直线只有3个交点,则平面被分成了 个部分.
14.如图,直线BE、CD相交于与点O,OF平分∠DOE,若∠DOF=20°,则∠BOC为 .
15.如图,直线AB、CD相交于O,∠COE是直角,∠1=48°,则∠2= .
16.如图,直线AB,CD相交于点O,OE⊥CD,∠BOE=38°,则∠AOC等于
度.
17.如图,∠1与∠2是同位角的是 .
18.如图,BC⊥AC,BC=12,AC=9,AB=15,则点C到线段AB的距离是 .
三.解答题(共7小题)
19.如图,A、B、C是平面内三点.
(1)按要求作图:
①作射线BC,过点B作直线l,使A、C两点在直线l两旁;
②点P为直线l上任意一点,点Q为直线BC上任意一点,连结线段AP、PQ;
(2)在(1)所作图形中,若点A到直线l的距离为2,点A到直线BC的距离为5,点A、B
之间的距离为8,点A、C之间的距离为6,则AP+PQ的最小值为 ,依据是 .
20.如图,直线AB和CD交于点O,∠COF=90°,OC平分∠AOE,∠COE=40°.
(1)求∠BOD的度数;
(2)OF平分∠BOE吗?请说明理由.
21.已知:直线AB与直线CD相交于点O,∠BOC=45°,
(1)如图1,若EO⊥AB,求∠DOE的度数;
(2)如图2,若EO平分∠AOC,求∠DOE的度数.
22.如图,直线AB,CD相交于点O,OF⊥CD,OE平分∠BOC.
(1)若∠BOE=60°,求∠AOE的度数;
(2)若∠BOD:∠BOE=4:3,求∠AOE的度数.
23.(1)如图①,OC是∠AOE内的一条射线,OB是∠AOC的平分线,OD是∠COE的平分线,∠AOE=120°,求∠BOD的度数;
(2)如图②,点A、O、E在一条直线上,OB是∠AOC的平分线,OD是∠COE的平分线,请说明OB⊥OD.
24.如图,在三角形ABC所在平面内画一条直线,使得与∠C成同旁内角的角有3个.若与∠C成同旁内角的角有4个,则该怎样画这条直线?
25.已知:如图是一个跳棋棋盘,其游戏规则是:一个棋子从某一个起始角开始,经过若干步跳动以后,到达终点角.跳动时,每一步只能跳到它的同位角或内错角或同旁内角的位置上,例如:从起始位置∠1跳到终点位置∠3写出其中两种不同路径,路径1:∠1﹣同旁内角→∠9﹣内错角→∠3.
路径2:∠1一内错角→∠12一内错角→∠6﹣同位角→∠10﹣同旁内角→∠3.
试一试:(1)从起始∠1跳到终点角∠8;
(2)从起始角∠1依次按同位角、内错角、同旁内角的顺序跳,能否跳到终点∠8?
参考答案与试题解析
一.选择题(共10小题)
1.解:①过两点有且只有一条直线,故①正确;
②两直线相交只有一个交点,故②正确;
③0的绝对值是它本身,故③正确;
④射线AB和射线BA的端点不同,延伸方向也不同,不是同一条射线,故④错误.
故选:C.
2.解:A.对顶角相等,说法正确;
B.两点确定一条直线,说法正确;
C.一个角的补角不一定大于这个角,比如∠A=150°,∠A的补角为30°,但是30°<150°,故原说法错误;
D.两点之间线段最短,说法正确.
故选:C.
3.解:根据垂线段最短得,能最快到达公路MN的小道是PB,
故选:B.
4.解:这四个图中,∠1与∠2有一条边在同一条直线上,另一条边在被截线的同一方,是同位角.
故选:D.
5.解:在平面内,过一点画已知直线的垂线,可画垂线的条数是1.
故选:B.
6.解:A、∠1与∠2是同旁内角,正确,不合题意;
B、∠1与∠6是内错角,正确,不合题意;
C、∠2与∠5是内错角,错误,符合题意;
D、∠3与∠5是同位角,正确,不合题意;
故选:C.
7.解:A、∠1和∠2是同旁内角,故本选项错误,符合题意;
B、∠2和∠3是同旁内角,故本选项正确,不符合题意;
C、∠1和∠4是同位角,故本选项正确,不符合题意;
D、∠3和∠4是邻补角,故本选项正确,不符合题意;
故选:A.
8.解:根据对顶角相等可知,C选项是正确的,
故选:C.
9.解:∵∠ACB=90°,CD⊥AB,垂足为D,
∴①AC与BC互相垂直,故①正确;
②CD与AB互相垂直,与AC不垂直,故②错误;
③点A到BC的垂线段是AC,故③错误;
④点C到AB的距离是CD的长,故④错误;
⑤线段BC的长度是点B到AC的距离,故⑤正确;
⑥线段BC的长是点B到AC的距离,故⑥错误;
故选:A.
10.解:根据同位角的定义可知D选项中∠1与∠2在直线的同侧,并且在第三条直线(截线)的同旁,故是同位角.
故选:D.
二.填空题(共8小题)
11.解:∵PM⊥MN,
∴由垂线段最短可知PM是最短的,
故答案为:PM,垂线段最短.
12.解:如图所示,直线AB与CD被直线AC所截得的内错角是∠3和∠4.
故答案是:∠3和∠4.
13.解:如图,
或
所以,平面内互不重合的4条直线只有3个交点,则平面被分成了 8或9个部分.
故答案是:8或9.
14.解:∵OF平分∠DOE,若∠DOF=20°,
∴∠DOE=2∠DOF=40°,
∴∠BOC=∠DOE=40°,
故答案为:40°.
15.解:∵∠COE是直角,∠1=48°,
∴∠2=180°﹣∠COE﹣∠1=180°﹣90°﹣48°=42°.
故答案为:42°.
16.解:∵OE⊥CD,
∴∠DOE=90°,
又∵∠BOE=38°,
∴∠BOC=90°+38°=128°,
则∠AOC=180°﹣∠BOC=52°.
故答案为:52.
17.解:这四个图中,∠1与∠2有一条边在同一条直线上,另一条边在被截线的同一方,是同位角,符合的有图①②.
故答案为:①②.
18.解:∵92+122=152,
∴AC2+BC2=AB2,
∴∠C=90°,
设点C到AB的距离是h, AC?BC=AB?h,
解得:h=7.2.
故答案为:7.2.
三.解答题(共7小题)
19.解:(1)①如图1所示,射线BC,直线l即为所求;
②如图1所示,线段AP,PQ即为所求;
(2)过A作AQ⊥BC交直线l于P,
则此时,AP+PQ的值最小,
∵点A到直线BC的距离为5,
∴AP+PQ的最小值为5,
依据是垂线段最短,
故答案为:5,垂线段最短.
20.解:(1)由∠COE=40°,OC平分∠AOE,
∠AOC=40°,
∠BOD=∠AOC=40°;
(2)OF平分∠BOE,理由如下:
由∠COE=40°,∠COF=90°
得∠EOF=90°﹣40°=50°,
又∵∠BOF=∠DOF﹣∠BOD=90°﹣40°=50°,
∴∠EOF=∠BOF,
∴OF平分∠BOE.
21.解:(1)∵直线AB与直线CD相交,
∴∠AOD=∠BOC=45°.
∵EO⊥AB,
∴∠AOE=90°,
∴∠DOE=∠AOD+∠AOE=135°;
(2)∵直线AB与直线CD相交,
∴∠AOD=∠BOC=45°,∠AOC=135°,
∵EO平分∠AOC,
∴∠AOE=∠AOC=67.5°,
∴∠DOE=∠AOD+∠AOE=112.5°.
22.解:(1)∵OE平分∠BOC,∠BOE=60°,
∴∠BOC=2∠BOE=120°,
∴∠AOC=180°﹣120°=60°=∠BOD,
∴∠AOE=60°+60°=120°;
(2)∵OE平分∠BOC,
∴∠BOD:∠BOE:∠EOC=4:3:3,
∴∠BOD=180°×=72°,
∴∠BOE=180°×=54°,
∴∠AOE=72°+54°=126°.
23.解:(1)∵OB是∠AOC的平分线∴
同理,
∴∠BOD=∠BOC+∠DOC=∠AOC+∠EOC=(∠AOC+∠EOC)=∠AOE,
∵∠AOE=120°
∴
(2)由(1)可知
∵∠AOE=180°
∴
∴OB⊥OD.
24.解:如图1,与∠C成同旁内角的角分别有3个,∠CED,∠B,∠A;
如图2,与∠C成同旁内角的角分别有4个,∠CFG,∠B,∠CGF,∠A.
25.解:(1)路径∠1∠12∠8;
(2)从起始角∠1依次按同位角、内错角、同旁内角的顺序跳,能跳到终点∠8.其路径为:
路径:∠1∠10∠5∠8.
