2019-2020学年北师大版数学七年级下册第2章《相交线与平行线》单元检测试题(含详细答案)
文档属性
| 名称 | 2019-2020学年北师大版数学七年级下册第2章《相交线与平行线》单元检测试题(含详细答案) |  | |
| 格式 | zip | ||
| 文件大小 | 208.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-21 22:46:20 | ||
图片预览



文档简介
2019-2020学年北师大版七年级下册第2章单元检测试题
满分120分
班级:_________姓名:_________学号:_________成绩:___________
一.选择题(共10小题,满分30分)
1.角52°18'的余角等于( )
A.37°42' B.38°42' C.127°42' D.128°42'
2.如图,点A到线段BC的距离指的是下列哪条线段的长度( )
A.AB B.AC C.AD D.AE
3.三条直线相交,交点最多有( )
A.1个 B.2个 C.3个 D.4个
4.下列说法错误的是( )
A.对顶角相等
B.两点之间所有连线中,线段最短
C.等角的补角相等
D.不相交的两条直线叫做平行线
5.如图,下列结论中错误的是( )
A.∠1与∠2是同旁内角 B.∠1与∠6是内错角
C.∠2与∠5是内错角 D.∠3与∠5是同位角
6.如图,下列条件能判断AD∥CB的是( )
A.∠2=∠3 B.∠1=∠4 C.∠1=∠2 D.∠3=∠4
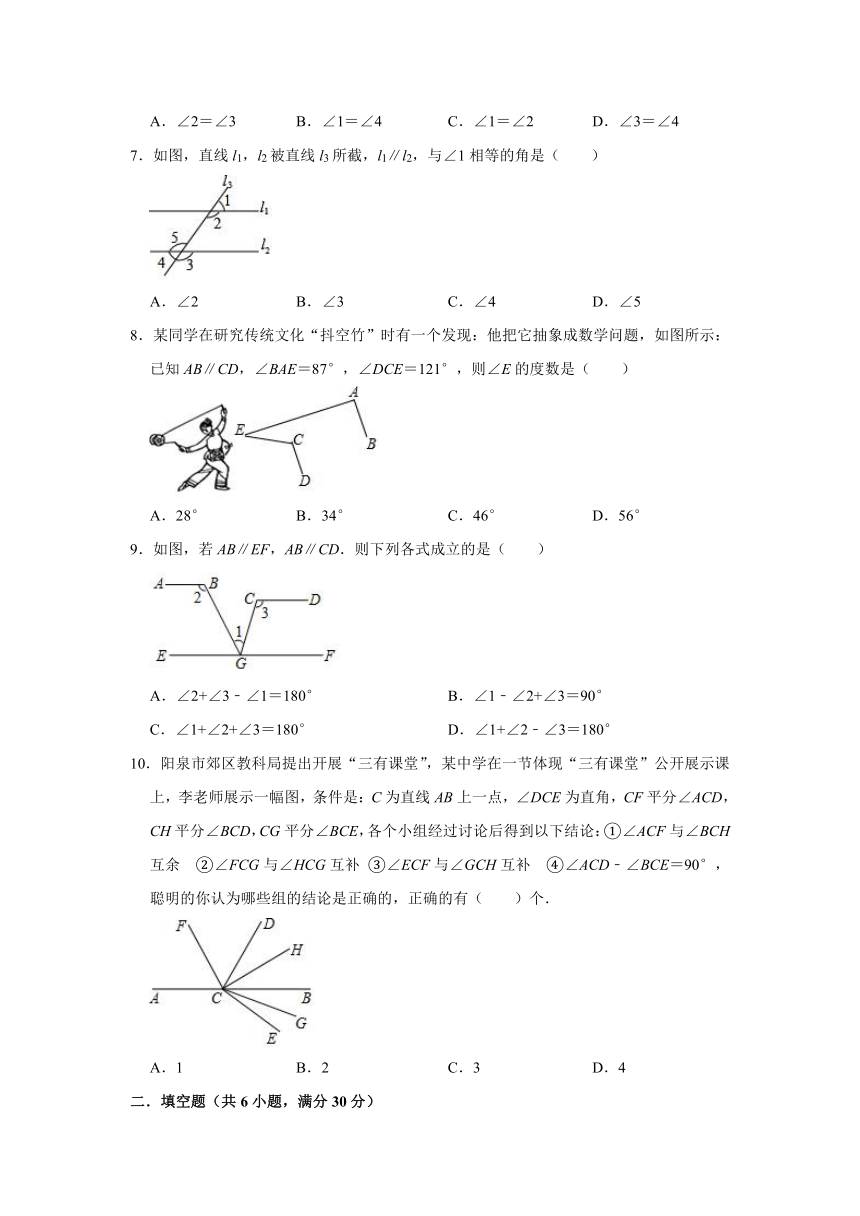
7.如图,直线l1,l2被直线l3所截,l1∥l2,与∠1相等的角是( )
A.∠2 B.∠3 C.∠4 D.∠5
8.某同学在研究传统文化“抖空竹”时有一个发现:他把它抽象成数学问题,如图所示:已知AB∥CD,∠BAE=87°,∠DCE=121°,则∠E的度数是( )
A.28° B.34° C.46° D.56°
9.如图,若AB∥EF,AB∥CD.则下列各式成立的是( )
A.∠2+∠3﹣∠1=180° B.∠1﹣∠2+∠3=90°
C.∠1+∠2+∠3=180° D.∠1+∠2﹣∠3=180°
10.阳泉市郊区教科局提出开展“三有课堂”,某中学在一节体现“三有课堂”公开展示课上,李老师展示一幅图,条件是:C为直线AB上一点,∠DCE为直角,CF平分∠ACD,CH平分∠BCD,CG平分∠BCE,各个小组经过讨论后得到以下结论:①∠ACF与∠BCH互余 ②∠FCG与∠HCG互补 ③∠ECF与∠GCH互补 ④∠ACD﹣∠BCE=90°,聪明的你认为哪些组的结论是正确的,正确的有( )个.
A.1 B.2 C.3 D.4
二.填空题(共6小题,满分30分)
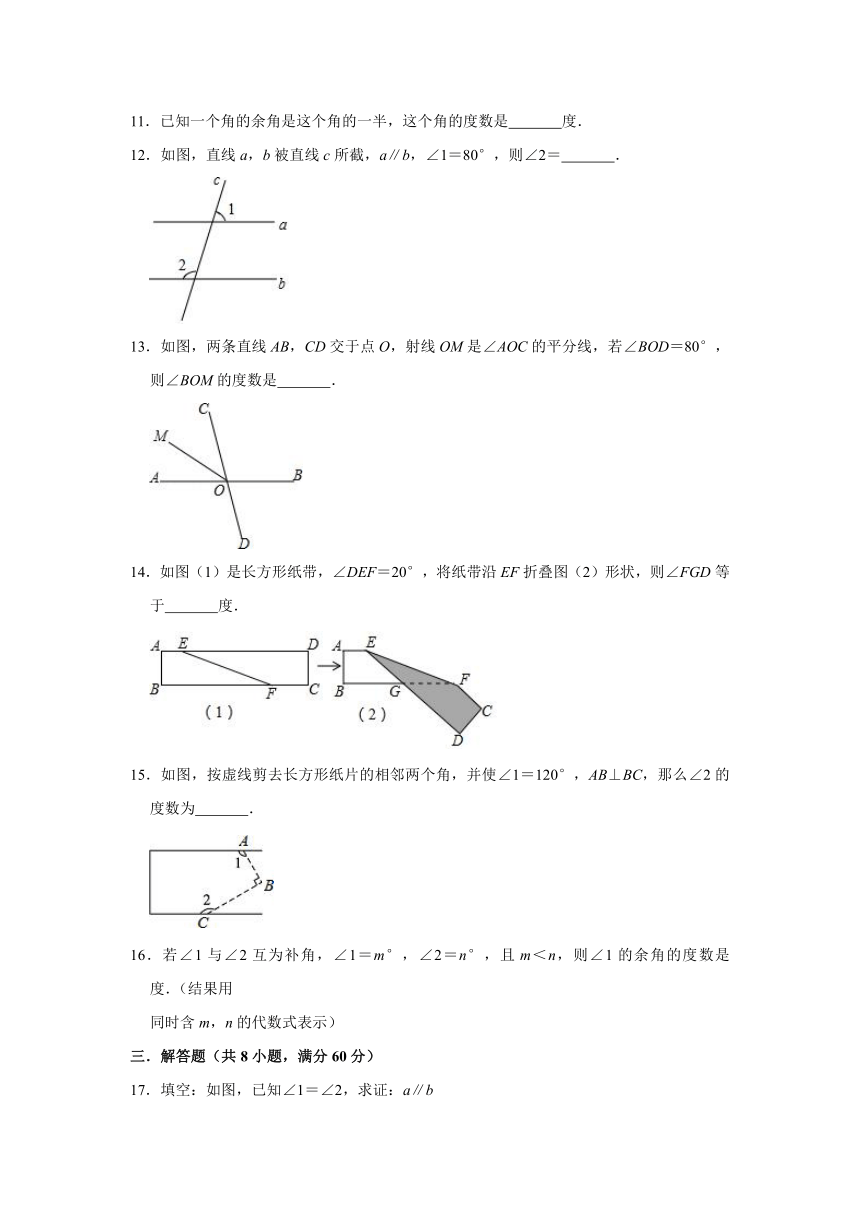
11.已知一个角的余角是这个角的一半,这个角的度数是 度.
12.如图,直线a,b被直线c所截,a∥b,∠1=80°,则∠2= .
13.如图,两条直线AB,CD交于点O,射线OM是∠AOC的平分线,若∠BOD=80°,则∠BOM的度数是 .
14.如图(1)是长方形纸带,∠DEF=20°,将纸带沿EF折叠图(2)形状,则∠FGD等于 度.
15.如图,按虚线剪去长方形纸片的相邻两个角,并使∠1=120°,AB⊥BC,那么∠2的度数为 .
16.若∠1与∠2互为补角,∠1=m°,∠2=n°,且m<n,则∠1的余角的度数是 度.(结果用
同时含m,n的代数式表示)
三.解答题(共8小题,满分60分)
17.填空:如图,已知∠1=∠2,求证:a∥b
证明:∵∠1=∠2(已知)
∠2=∠3( )
∴∠1= ( )
∴a∥b( )
18.我们经常运用“方程”的思想方法解决问题.
已知∠1是∠2的余角,∠2是∠3的补角,若∠1+∠3=130°,求∠2的度数.
可以进行如下的解题:(请完成以下解题过程)
解:设∠2的度数为x,
则∠1= °,∠3= °.
根据“ ”
可列方程为: .
解方程,得x= .
故:∠2的度数为 °.
19.已知点A,B,C如图所示,根据要求完成下列各题.
(1)画直线BC,线段AB和射线CA.
(2)过点A画BC的垂线段AD,垂足为D,并量出点A到直线BC的距离为 cm.(以答题纸为测量依据,结果精确到0.1cm).
20.如图,已知直线AB、CD交于点O,OE⊥AB,OF平分∠DOB,∠EOF=70°.求∠AOC的度数.
21.如图,∠EBC+∠EFA=180°,∠A=∠C.求证:AB∥CE.
22.阅读理解,补全证明过程及推理依据.
已知:如图,点E在直线DF上,点B在直线AC上,∠1=∠2,∠3=∠4.
求证∠A=∠F
证明:∵∠1=∠2(已知)
∠2=∠DGF( )
∴∠1=∠DGF(等量代换)
∴ ∥ ( )
∴∠3+∠ =180°( )
又∵∠3=∠4(已知)
∴∠4+∠C=180°(等量代换)
∴ ∥ ( )
∴∠A=∠F( )
23.已知:如图所示,OD平分∠BOC,OE平分∠AOC.若∠BOC=70°,∠AOC=50°.
(1)求出∠AOB及其补角的度数;
(2)求出∠DOC和∠AOE的度数,并判断∠DOE与∠AOB是否互补,并说明理由;
(3)若∠BOC=α,∠AOC=β,则∠DOE与∠AOB是否互补,并说明理由.
24.课题学习:平行线的“等角转化功能.
(1)问题情景:如图1,已知点A是BC外一点,连接AB、AC,求∠BAC+∠B+∠C的度数.
天天同学看过图形后立即想出:∠BAC+∠B+∠C=180°,请你补全他的推理过程.
解:(1)如图1,过点A作ED∥BC,∴∠B= ,∠C= .
又∵∠EAB+∠BAC+∠CAD=180°,∴∠BAC+∠B+∠C=180°.
解题反思:从上面的推理过程中,我们发现平行线具有“等角转化”功能,将∠BAC,∠B,∠C“凑”在一起,得出角之间的关系,使问题得以解决.
(2)问题迁移:如图2,AB∥ED,求∠B+∠BCD+∠D的度数.
(3)方法运用:如图3,AB∥CD,点C在D的右侧,∠ADC=70°,点B在A的左侧,∠ABC=60°,BE平分∠ABC,DE平分∠ADC,BE、DE所在的直线交于点E,点E在AB与CD两条平行线之间,求∠BED的度数.
参考答案
一.选择题(共10小题)
1.【解答】解:根据题意,得
90°﹣52°18′=37°42′,
故选:A.
2.【解答】解:由图可得,AD⊥BC于D,点A到线段BC的距离指线段AD的长,
故选:C.
3.【解答】解:如图:
,
交点最多3个,
故选:C.
4.【解答】解:A、对顶角相等,正确;
B、两点之间所有连线中,线段最短,正确;
C、等角的补角相等,正确;
D、在同一平面内,不相交的两条直线叫做平行线,故本选项错误;
故选:D.
5.【解答】解:A、∠1与∠2是同旁内角,正确,不合题意;
B、∠1与∠6是内错角,正确,不合题意;
C、∠2与∠5是内错角,错误,符合题意;
D、∠3与∠5是同位角,正确,不合题意;
故选:C.
6.【解答】解:A、∠2=∠3,则AB∥DC,故选项错误;
B、∠1=∠4,则AD∥CB,故选项正确;
C、∠1=∠2,不能判定,故选项错误;
D、∠3=∠4,不能判定,故选项错误.
故选:B.
7.【解答】解:∵l1∥l2,
∴∠6=∠1,
∵∠6=∠4,
∴与∠1相等的角是∠4.
故选:C.
8.【解答】解:如图,延长DC交AE于F,
∵AB∥CD,∠BAE=87°,
∴∠CFE=87°,
又∵∠DCE=121°,
∴∠E=∠DCE﹣∠CFE=121°﹣87°=34°,
故选:B.
9.【解答】解:∵AB∥EF,AB∥CD,
∴EF∥CD,
∴∠3=∠CGE,
∴∠3﹣∠1=∠CGE﹣∠1=∠BGE,
∵AB∥EG,
∴∠2+∠BGE=180°,
即∠2+∠3﹣∠1=180°,
故选:A.
10.【解答】解:∵CF平分∠ACD,CH平分∠BCD,CG平分∠BCE,
∴∠ACF=∠FCD=∠ACD,∠DCH=∠HCB=∠DCB,∠BCG=∠ECG=∠BCE,
∵∠AOB=180°,∠DCE=90°,
∴∠FCH=90°,∠HCG=45°,∠FCG=135°
∴∠ACF+∠BCH=90°,∠FCG+∠HCG=180°,故①②正确,
∵∠ECF=∠DCE+∠FCD=90°+∠FCD,∠FCD+∠DCH=90°,
∴∠ECF+∠DCH=180°,
∵∠HCG≠∠DCH,
∴∠ECF与∠GCH不互补,故③错误,
∵∠ACD﹣∠BCE=180°﹣∠DCB﹣∠BCE=90°,故④正确.
故选:C.
二.填空题(共6小题)
11.【解答】解:设这个角为α,
根据题意得,90°﹣α=α,
解得α=60°.
故答案为:60.
12.【解答】解:∵∠1=80°,
∴∠3=80°.
∵a∥b,
∴∠2+∠3=180°,
∴∠2=180°﹣80°=100°.
故答案为:100°.
13.【解答】解:∵∠BOD=80°,
∴∠AOC=80°,∠COB=100°,
∵射线OM是∠AOC的平分线,
∴∠COM=40°,
∴∠BOM=40°+100°=140°,
故答案为:140°.
14.【解答】解:根据折叠可知:
∠AEG=180°﹣20°×2=140°,
∵AE∥BF,
∴∠EGB=180°﹣∠AEG=40°,
∴∠FGD=40°.
故答案为:40.
15.【解答】解:如图,过点B作长方形边的平行线,
∵长方形对边平行,
∴∠1+∠ABD=180°,∠2+∠CBD=180°,
∴∠1+∠ABC+∠2=360°;
∵AB⊥BC,
∴∠ABC=90°,
∴∠2=360°﹣120°﹣90°=150°.
故答案为:150°
16.【解答】解:∵∠1与∠2互为补角,∠1=m°,∠2=n°,且m<n,
∴m+n=180,
∴=90,
∴∠1的余角的度数是﹣m=.
故答案为:.
三.解答题(共8小题)
17.【解答】证明:∵∠1=∠2(已知)
∠2=∠3(对顶角相等)
∴∠1=∠3(等量代换)
∴a∥b(同位角相等,两直线平行),
故答案为:对顶角相等;∠3;等量代换;同位角相等,两直线平行
18.【解答】解:设∠2的度数为x,
则∠1=(90﹣x)°,∠3=(180﹣x)°.
根据“∠1+∠3=130°”
可列方程为:(90﹣x)+(180﹣x)=130.
解方程,得x=70.
故:∠2的度数为70°.
故答案为:(90﹣x);(180﹣x);∠1+∠3=130°;(90﹣x)+(180﹣x)=130;70;70.
19.【解答】解:(1)如图所示:
(2)经测量AD=1.8cm,
故答案为:1.8.
20.【解答】解:∵OE⊥AB,∠EOF=70°,
∴∠BOF=20°,
∵OF平分∠DOB,
∴∠DOB=40°,
∴∠AOC=∠DOB=40°.
21.【解答】证明:∵∠EBC+∠EFA=180°,∠DFB=∠EFA,
∴∠EBC+∠DFB=180°,
∴BC∥AD,
∴∠EDA=∠C.
∵∠A=∠C,
∴∠EDA=∠A,
∴AB∥CE.
22.【解答】解:∵∠1=∠2(已知)
∠2=∠DGF (对顶角相等)
∴∠1=∠DGF( 等量代换 )
∴BD∥CE (同位角相等,两直线平行)
∴∠3+∠C=180° (两直线平行,同旁内角互补)
又∵∠3=∠4(已知)
∴∠4+∠C=180°
∴AC∥DF(同旁内角互补,两直线平行)
∴∠A=∠F (两直线平行,内错角相等);
故答案为:对顶角相等;BD;CE;同位角相等,两直线平行;C;两直线平行,同旁内角互补;AC,DF;同旁内角互补,两直线平行;两直线平行,内错角相等.
23.【解答】解:(1)∠AOB=∠BOC+∠AOC=70°+50°=120°,
其补角为180°﹣∠AOB=180°﹣120°=60°,
(2)∠DOE与∠AOB互补,理由如下:
∵∠DOC=∠BOC=×70°=35°,∠COE=∠AOC=×50°=25°.
∴∠DOE=∠DOC+∠COE=35°+25°=60°.
∴∠DOE+∠AOB=60°+70°+70°=180°,
∴∠DOE与∠AOB互补.
(3)∠DOE与∠AOB不互补,理由如下:
∵∠DOC=∠BOC=α,∠COE=∠AOC=β,
∴∠DOE=∠DOC+∠COE=α+β=(α+β),
∴∠DOE+∠AOB=(α+β)+(α+β)=(α+β),
∴∠DOE与∠AOB不互补.
24.【解答】解::(1)∵ED∥BC,
∴∠B=∠EAB,∠C=∠DAC,
(2)∵AB∥DE,
∴CF∥DE,
∴∠D=∠FCD,
∵CF∥AB,
∴∠B=∠BCF,
∵∠BCF+∠BCD+∠DCF=360°,
∴∠B+∠BCD+∠D=360°,
(3)如图3,过点E作EF∥AB,
∵AB∥CD,∴AB∥CD∥EF,
∴∠ABE=∠BEF,∠CDE=∠DEF,
∵BE平分∠ABC,DE平分∠ADC,∠ABC=60°,∠ADC=70°,
∴∠ABE=∠ABC=30°,∠CDE=∠ADC=35°
∴∠BED=∠BEF+∠DEF=30°+35°=65°.
故答案为:∠EAB,∠DAC.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
