苏科版八年级数学下册9.1图形的旋转教案+巩固练习(无答案)
文档属性
| 名称 | 苏科版八年级数学下册9.1图形的旋转教案+巩固练习(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 177.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-23 00:00:00 | ||
图片预览

文档简介
9.1图形的旋转教案
情境引入:
生活中的数学
1.PPT展示一组生活中的图片:电梯上升、叠纸回顾图形的平移和翻折运动;
2.PPT展示另一组图片:秋千、钟表、风车
(1)观察这组图片,你发现 了哪些图形的运动?
(2)这些旋转现象有什么共同的特征?
(3)生活中还有类似的例子吗?
将图中的生活情境转化成几何图形的运动,引出课题:图形的旋转。
新课指导:
操作与思考
1.将三角形纸片绕直角顶点C按逆时针方向旋转一定的角度,再画下它的外轮廓,记为△A’B’C .动画演示给出概念:
图形的旋转:将图形绕一个定点转动一定的角度,这样的图形运动称为图形的旋转.这个定点称为旋转中心,旋转的角度称为旋转角。
2.将△ABC绕点C按逆时针方向旋转 到△DEC的位置
问题1.找出图中的旋转中心和旋转角.
问题2 在三角尺ABC的旋转过程中,
哪些发生了变化?哪些没有发生变化?
图形的旋转不改变图形的形状、大小。
3.如图,△A'OB'是△AOB绕点O按逆时针方向旋转45度所得的。
感受对应顶点对应线段,指出对称中心和旋转角。
一个图形和它经过旋转所得到的图形中,对应点到旋转中心的距离相等,两组对应点分别与旋转中心连线所成的角相等.
理解与应用:
例题 如图,
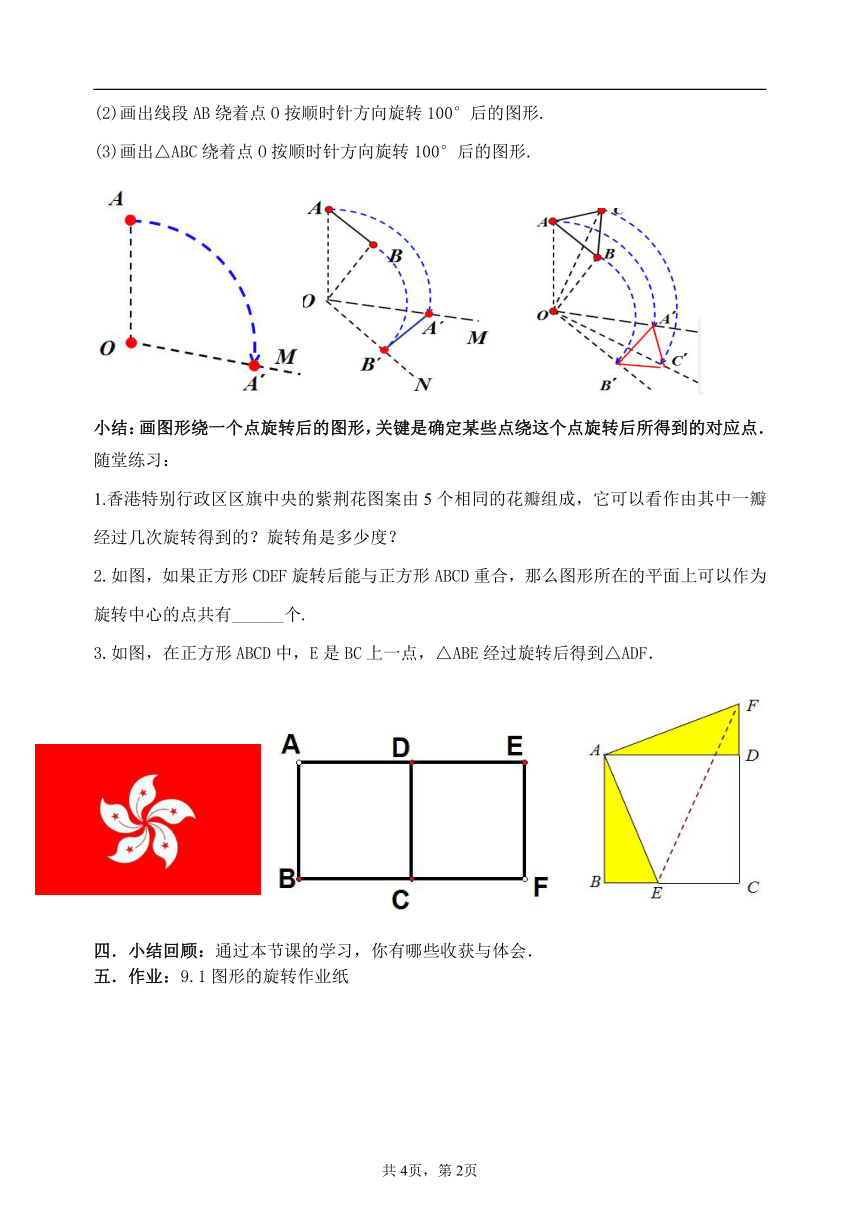
(1)画出点A绕着点O按顺时针方向旋转100°后的点A′.
(2)画出线段AB绕着点O按顺时针方向旋转100°后的图形.
(3)画出△ABC绕着点O按顺时针方向旋转100°后的图形.
小结:画图形绕一个点旋转后的图形,关键是确定某些点绕这个点旋转后所得到的对应点.
随堂练习:
1.香港特别行政区区旗中央的紫荆花图案由5个相同的花瓣组成,它可以看作由其中一瓣经过几次旋转得到的?旋转角是多少度?
如图,如果正方形CDEF旋转后能与正方形ABCD重合,那么图形所在的平面上可以作为旋转中心的点共有______个.
3.如图,在正方形ABCD中,E是BC上一点,△ABE经过旋转后得到△ADF.
四.小结回顾:通过本节课的学习,你有哪些收获与体会.
五.作业:9.1图形的旋转作业纸
9.1图形的旋转
班级 学号 姓名 等第____________
【基础巩固】1. 在平面内,将一个图形绕定点旋转一定的角度,这样的图形运动称为 . 2. 旋转不改变图形的 和 .3. 如图,△ABC与△ACD都是等边三角形,如果△ABC经过旋转后能与△ACD重合,则旋转中心是 ,旋转角为 .(注:只需填上你认为正确的一种条件即可,不必考虑所有可能的情形.) (第3题) (第4题) (第5题) 4.上图形绕着中心至少旋转 度能与自身重合. 5.△ABC和△DCE是等边三角形,则在此图中,△ACE绕着 点 旋转 度可得到△ . 6.下列图形中,绕某个点旋转能与自身重合的有 ( )①正方形; ②长方形; ③等边三角形;④线段;⑤角;⑥平行四边形.A. 5个 B. 2个 C. 3个 D. 4个7. 如图,△BDE是由等边三角形ABC绕着B点按逆时针方向旋转30°得到的.按图回答: (1)点A、B、C的对应点分别是: _______ 、 _______、________ ; (2)线段AB、AC、BC的对应线段分别是: _______、 _________、 ________; (3)∠A、∠C和∠ABC的对应角分别是: _______ 、 _________、 ________.如图,四边形ABCD是正方形,△ADF通过旋转可得到△ABE,AF=4,AB=7. (1) 旋转中心是_________,旋转角=_________. (2) DE=_____ , BE与DF的位置关系:_______. 【拓展延伸】9.如图:正方形ABCD是由正方形ABCD旋转而成.(1) 旋转中心是:_____ . (2) 旋转的角度=_______°. (3) 若正方形的边长是1,求CD的长. 10.画出△ABC绕点O按逆时针旋转90度后的对应三角形. 【自主预习】 1.阅读课本P59-60; 2. 一个图形绕者某一点旋转 ,如果它能够与另一个图形 ,那么称这两个图形关于这点 ,也称这两个图形成 ,这个点叫做 . 成长记录
A
C
D
E
B
共2页,第2页
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
