2020春湘教版八下数学1.4角平分线的性质教学课件(17张)
文档属性
| 名称 | 2020春湘教版八下数学1.4角平分线的性质教学课件(17张) |

|
|
| 格式 | zip | ||
| 文件大小 | 367.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-22 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
教学课件
数学 八年级下册 湘教版
第1章 直角三角形
1.4 角平分线的性质
回忆旧知
角平分线是以一个角的顶点为端点的一条射线,它把这个角分成两个相等的角.
新知探究
如图,在∠AOB的平分线OC上任取一点P,作PD⊥OA,PE⊥OB,垂足分别为D,E,试问PD与PE相等吗?
A
B
O
P
C
将∠AOB沿OC对折,可以发现PD与PE重合,即PD与PE相等.
D
E
解 ∵PD⊥OA,PE⊥OB,
∴∠PDO=∠PEO=90°.
在△PDO和△PEO中,
∵∠PDO=∠PEO,
∠DOP=∠EOP,
OP=OP,
∴△PDO≌△PEO.
∴PD=PE.
角平分线上的点到角的两边
的距离相等.
由此得到角平分线的性质定理:
O
E
P
D
A
C
B
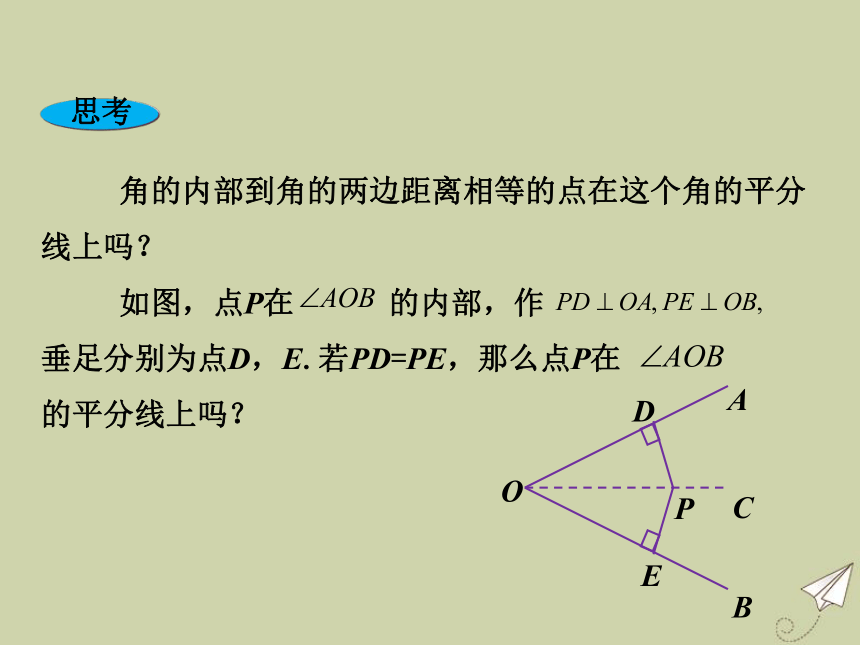
思考
角的内部到角的两边距离相等的点在这个角的平分线上吗?
如图,点P在 的内部,作 垂足分别为点D,E.若PD=PE,那么点P在 的平分线上吗?
如图,过点O,P作射线OC.
∵PD⊥OA,PE⊥OB,
∴∠PDO=∠PEO=90°.
在Rt△PDO和Rt△PEO中,
∵OP=OP,PD=PE,
∴Rt△PDO≌Rt△PEO.
∴∠AOC=∠BOC.
∴OC是∠AOB的平分线,
即点P在∠AOB的平分线OC上.
角的内部到角的两边距离相等的点在角的平分线上.
由此得到角平分线的性质定理的逆定理:
【例1】如图,∠BAD=∠BCD=90°,∠1=∠2.
(1)求证:点B在∠ADC的平分线上;
(2)求证:BD平分∠ABC.
A
B
C
D
1
2
证明:(1)在△ABC中,
∵∠1=∠2,
∴BA=BC.
又BA⊥AD,BC⊥CD,
∴点B在∠ADC的平分线上.
(2)在Rt△BAD和Rt△BCD中,
∵BA=BC,BD=BD,
∴Rt△BAD ≌ Rt△BCD.
∴∠ABD=∠CBD.
∴BD平分∠ABC.
1.如图,在直线MN上求作一点P,使点P到∠AOB两边的距离相等.
B
A
O
M
N
解:如图.
P
练习
2.如图,在△ABC中,AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F,BD=CD.
求证:AB=AC.
A
B
C
D
E
F
证明:∵AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F,
∴DE=DF.
∵BD=CD,
∴Rt△DBE≌Rt△DCF.
∴∠B=∠C.
∴AB=AC.
如图,已知EF⊥CD,EF⊥AB,MN⊥AC,M是EF的中点.需添加一个什么条件,就可使CM,AM分别为∠ACD和∠CAB的平分线呢?
C
D
B
A
E
F
M
N
可以添加条件MN=ME(或MN=MF).
∵ME⊥CD,MN⊥CA,
∴M在∠ACD的平分线上,
即CM是∠ACD的平分线.
同理可得AM是∠CAB的平分线.
思考
【例2】如图,在△ABC的外角∠DAC的平分线上任取一点P,作PE⊥DB,PF⊥AC,垂足分别为E,F.试探索BE+PF与PB的大小关系.
解 ∵AP是∠DAC的平分线,
又PE⊥DB,PF⊥AC,
∴PE=PF.
在△EBP中,BE+PE>PB,
∴BE+PF>PB.
如图,你能在△ABC中找到一点P,使其到三边的距离相等吗?
A
B
C
因为角平分线上的点到角的两边的距离相等,所以只要作△ABC任意两角(例如∠A与∠B)的平分线,其交点P即为所求作的点.点P也在∠C的平分线上,如图.
P
思考
3.E是∠AOB的平分线上一点,EC⊥OA于点C,
ED⊥OB于点D,求证:(1)∠ECD=∠EDC;
(2)OC=OD.
A
B
O
C
D
E
证明:(1)∵E是∠AOB的平分线上一点,
EC⊥OA于点C,ED⊥OB于点D,
∴CE=DE.∴∠ECD=∠EDC.
(2)在Rt△COE和Rt△DOE中,
CE=DE,OE=OE.
∴Rt△COE≌Rt△DOE(HL).
∴OC=OD.
练习
4.如图,在△ABC中,AD⊥DE,BE⊥DE,AC,BC分别平分∠BAD,∠ABE,点C在线段DE上.
求证:AB=AD+BE.
A
B
C
D
E
证明:过点C作CF⊥AB于点F.
∵AC,BC分别平分∠BAD,∠ABE,
且AD⊥DE,BE⊥DE,
∴DC=CF,CE=CF.
∴Rt△ACD≌Rt△ACF(HL),Rt△BCE≌Rt△BCF(HL).
∴AD=AF,BE=BF.
∴AB=AF+BF=AD+BE.
通过本节课,你有什么收获?
你还存在哪些疑问,和同伴交流.
我思 我进步
教学课件
数学 八年级下册 湘教版
第1章 直角三角形
1.4 角平分线的性质
回忆旧知
角平分线是以一个角的顶点为端点的一条射线,它把这个角分成两个相等的角.
新知探究
如图,在∠AOB的平分线OC上任取一点P,作PD⊥OA,PE⊥OB,垂足分别为D,E,试问PD与PE相等吗?
A
B
O
P
C
将∠AOB沿OC对折,可以发现PD与PE重合,即PD与PE相等.
D
E
解 ∵PD⊥OA,PE⊥OB,
∴∠PDO=∠PEO=90°.
在△PDO和△PEO中,
∵∠PDO=∠PEO,
∠DOP=∠EOP,
OP=OP,
∴△PDO≌△PEO.
∴PD=PE.
角平分线上的点到角的两边
的距离相等.
由此得到角平分线的性质定理:
O
E
P
D
A
C
B
思考
角的内部到角的两边距离相等的点在这个角的平分线上吗?
如图,点P在 的内部,作 垂足分别为点D,E.若PD=PE,那么点P在 的平分线上吗?
如图,过点O,P作射线OC.
∵PD⊥OA,PE⊥OB,
∴∠PDO=∠PEO=90°.
在Rt△PDO和Rt△PEO中,
∵OP=OP,PD=PE,
∴Rt△PDO≌Rt△PEO.
∴∠AOC=∠BOC.
∴OC是∠AOB的平分线,
即点P在∠AOB的平分线OC上.
角的内部到角的两边距离相等的点在角的平分线上.
由此得到角平分线的性质定理的逆定理:
【例1】如图,∠BAD=∠BCD=90°,∠1=∠2.
(1)求证:点B在∠ADC的平分线上;
(2)求证:BD平分∠ABC.
A
B
C
D
1
2
证明:(1)在△ABC中,
∵∠1=∠2,
∴BA=BC.
又BA⊥AD,BC⊥CD,
∴点B在∠ADC的平分线上.
(2)在Rt△BAD和Rt△BCD中,
∵BA=BC,BD=BD,
∴Rt△BAD ≌ Rt△BCD.
∴∠ABD=∠CBD.
∴BD平分∠ABC.
1.如图,在直线MN上求作一点P,使点P到∠AOB两边的距离相等.
B
A
O
M
N
解:如图.
P
练习
2.如图,在△ABC中,AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F,BD=CD.
求证:AB=AC.
A
B
C
D
E
F
证明:∵AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F,
∴DE=DF.
∵BD=CD,
∴Rt△DBE≌Rt△DCF.
∴∠B=∠C.
∴AB=AC.
如图,已知EF⊥CD,EF⊥AB,MN⊥AC,M是EF的中点.需添加一个什么条件,就可使CM,AM分别为∠ACD和∠CAB的平分线呢?
C
D
B
A
E
F
M
N
可以添加条件MN=ME(或MN=MF).
∵ME⊥CD,MN⊥CA,
∴M在∠ACD的平分线上,
即CM是∠ACD的平分线.
同理可得AM是∠CAB的平分线.
思考
【例2】如图,在△ABC的外角∠DAC的平分线上任取一点P,作PE⊥DB,PF⊥AC,垂足分别为E,F.试探索BE+PF与PB的大小关系.
解 ∵AP是∠DAC的平分线,
又PE⊥DB,PF⊥AC,
∴PE=PF.
在△EBP中,BE+PE>PB,
∴BE+PF>PB.
如图,你能在△ABC中找到一点P,使其到三边的距离相等吗?
A
B
C
因为角平分线上的点到角的两边的距离相等,所以只要作△ABC任意两角(例如∠A与∠B)的平分线,其交点P即为所求作的点.点P也在∠C的平分线上,如图.
P
思考
3.E是∠AOB的平分线上一点,EC⊥OA于点C,
ED⊥OB于点D,求证:(1)∠ECD=∠EDC;
(2)OC=OD.
A
B
O
C
D
E
证明:(1)∵E是∠AOB的平分线上一点,
EC⊥OA于点C,ED⊥OB于点D,
∴CE=DE.∴∠ECD=∠EDC.
(2)在Rt△COE和Rt△DOE中,
CE=DE,OE=OE.
∴Rt△COE≌Rt△DOE(HL).
∴OC=OD.
练习
4.如图,在△ABC中,AD⊥DE,BE⊥DE,AC,BC分别平分∠BAD,∠ABE,点C在线段DE上.
求证:AB=AD+BE.
A
B
C
D
E
证明:过点C作CF⊥AB于点F.
∵AC,BC分别平分∠BAD,∠ABE,
且AD⊥DE,BE⊥DE,
∴DC=CF,CE=CF.
∴Rt△ACD≌Rt△ACF(HL),Rt△BCE≌Rt△BCF(HL).
∴AD=AF,BE=BF.
∴AB=AF+BF=AD+BE.
通过本节课,你有什么收获?
你还存在哪些疑问,和同伴交流.
我思 我进步
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
