苏科版2019-2020学年七年级下册第8章幂的运算单元检测卷(带详细答案)
文档属性
| 名称 | 苏科版2019-2020学年七年级下册第8章幂的运算单元检测卷(带详细答案) |  | |
| 格式 | zip | ||
| 文件大小 | 122.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-22 16:56:49 | ||
图片预览



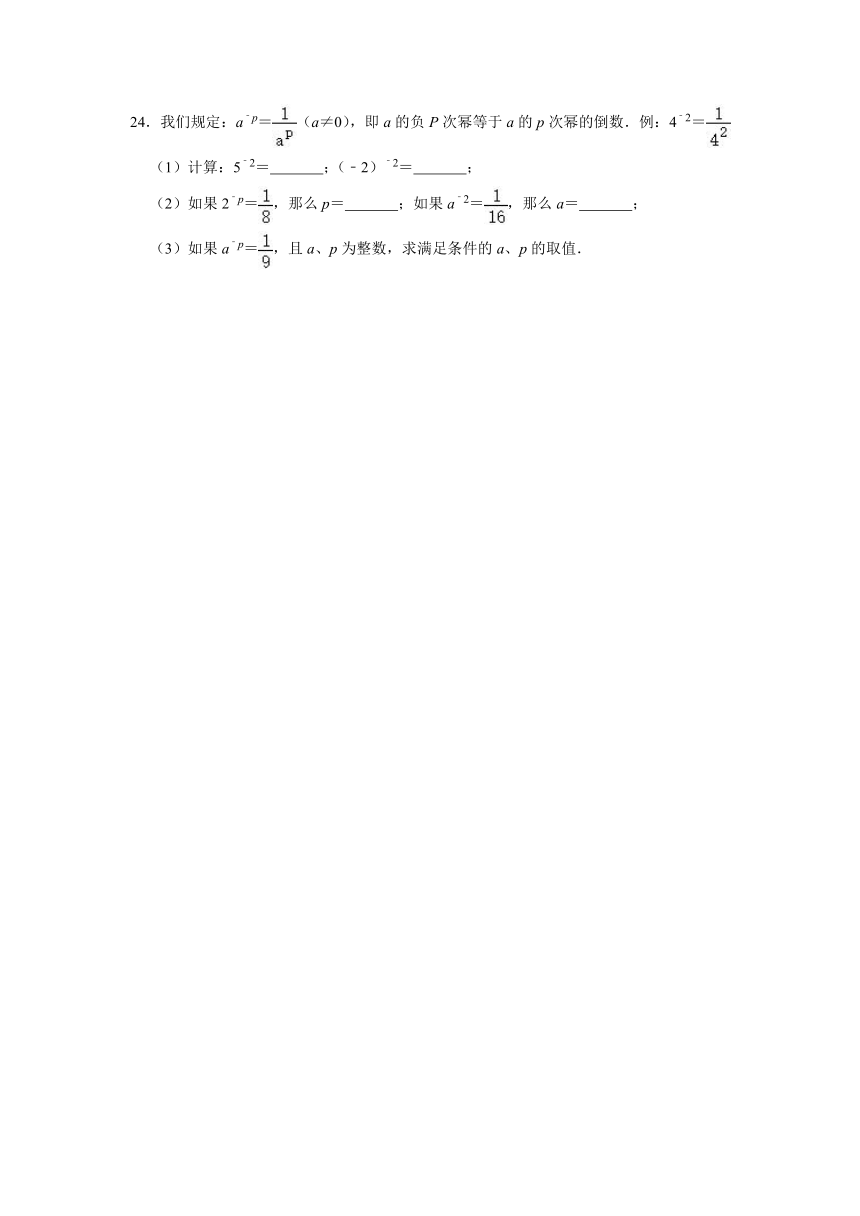
文档简介
苏科版2019-2020学年七年级下册第8章《幂的运算》单元检测卷
满分120分
姓名________班级________成绩_________
一.选择题(共10小题,满分30分)
1.计算b?b2的结果是( )
A.b3 B.b2 C.b D.1
2.某种计算机完成一次基本运算的时间约为1纳秒(ns),已知1纳秒=0.000 000 001秒,该计算机完成15次基本运算,所用时间用科学记数法表示为( )
A.1.5×10﹣9秒 B.15×10﹣9秒 C.1.5×10﹣8秒 D.15×10﹣8秒
3.已知:2m=1,2n=3,则2m+n=( )
A.2 B.3 C.4 D.6
4.下列运算正确的是( )
A.3a2﹣a2=2a4 B.a÷a=0
C.a2?a3=a5 D.(﹣a2b)3=a6b3
5.计算x5m+3n+1÷(xn)2?(﹣xm)2的结果是( )
A.﹣x7m+n+1 B.x7m+n+1 C.x7m﹣n+1 D.x3m+n+1
6.当a<0,n为正整数时,(﹣a)5?(﹣a)2n的值为( )
A.正数 B.负数 C.非正数 D.非负数
7.若A为一数,且A=25×76×114,则下列选项中所表示的数,何者是A的因子?( )
A.24×5 B.77×113 C.24×74×114 D.26×76×116
8.化简(x﹣1﹣1)﹣1的结果是( )
A. B. C.x﹣1 D.1﹣x
9.如果a=(﹣99)0,b=(﹣0.1)﹣1,c=,那么a、b、c的大小关系为( )
A.a>b>c B.c>a>b C.a>c>b D.c>b>a
10.我们规定:a⊕b=10a×10b,例如3⊕4=103×104=107,则12⊕3的值为( )
A.1036 B.1015 C.109 D.104
二.填空题(共6小题,满分24分)
11.科学家发现一种病毒的直径为0.000104米,用科学记数法表示为 米.
12.计算:(﹣2020)0+3﹣1= .
13.已知2x=3,2y=5,则22x+y﹣1= .
14.将代数式2﹣1x﹣3y2化为只含有正整数指数幂的形式 .
15.若2x﹣5y﹣3=0,则4x÷32y的值为 .
16.定义一种新运算:n?xn﹣1dx=an﹣bn,例如:2?xdx=k2﹣h2,若﹣x﹣2dx=﹣2,则m= .
三.解答题(共8小题,满分66分)
17.计算:.
18.计算:(a﹣b)3?(b﹣a)3+[2(a﹣b)2]3.
19.已知2a=4,2b=6,2c=12
(1)求证:a+b﹣c=1;
(2)求22a+b﹣c的值.
20.已知a+b=,且a是大于﹣6的整数,b是大于﹣1的分数,求(ab)3的值.
21.阅读材料:
(1)1的任何次幂都为1:
(2)﹣1的奇数次幂为﹣1:
(3)﹣1的偶数次幂为1:
(4)任何不等于零的数的零次幂为1.
请问当x为何值时,代数式(2x+3)x+2020的值为1.
22.规定两数a,b之间的一种新运算※,如果ac=b,那么a※b=c.
例如:因为52=25,所以5※25=2,因为50=1,所以5※1=0.
(1)根据上述规定,填空:2※8= 2※= .
(2)在运算时,按以上规定:设4※5=x,4※6=y,请你说明下面这个等式成立:4※5+4※6=4※30.
23.规定两数a,b之间的一种运算,记作(a,b):如果ac=b,那么(a,b)=c.
例如:因为23=8,所以(2,8)=3.
(1)根据上述规定,填空:
(3,27)= ,(5,1)= ,(2,)= .
(2)小明在研究这种运算时发现一个现象:(3n,4n)=(3,4),小明给出了如下的证明:设(3n,4n)=x,则(3n)x=4n,即(3x)n=4n
所以3x=4,即(3,4)=x,
所以(3n,4n)=(3,4).
请你尝试运用这种方法证明下面这个等式:(3,4)+(3,5)=(3,20)
24.我们规定:a﹣p=(a≠0),即a的负P次幂等于a的p次幂的倒数.例:4﹣2=
(1)计算:5﹣2= ;(﹣2)﹣2= ;
(2)如果2﹣p=,那么p= ;如果a﹣2=,那么a= ;
(3)如果a﹣p=,且a、p为整数,求满足条件的a、p的取值.
参考答案
一.选择题(共10小题)
1.【解答】解:b?b2=b3.
故选:A.
2.【解答】解:所用时间=15×0.000 000 001=1.5×10﹣8.
故选:C.
3.【解答】解:∵2m=1,2n=3,
∴2m+n=2m?2n=1×3=3.
故选:B.
4.【解答】解:A、3a2﹣a2=2a2,故此选项错误;
B、a÷a=1(a≠0),故此选项错误;
C、a2?a3=a5,正确;
D、(﹣a2b)3=﹣a6b3,故此选项错误;
故选:C.
5.【解答】解:x5m+3n+1÷(xn)2?(﹣xm)2=x5m+3n+1÷x2n?x2m=x5m+3n+1﹣2n+2m=x7m+n+1.
故选:B.
6.【解答】解:∵(﹣a)5?(﹣a)2n=(﹣a)2n+5,
又∵a<0,n为正整数,
∴﹣a>0,
∴(﹣a)5?(﹣a)2n=(﹣a)2n+5>0,是正数.
故选:A.
7.【解答】解:∵A=25×76×114=24×74×114(2×72),
∴24×74×114,是原式的因子.
故选:C.
8.【解答】解:原式=(﹣1)﹣1
=()﹣1
=.
故选:A.
9.【解答】解:a=(﹣99)0=1,
b=(﹣0.1)﹣1=﹣10,
c=(﹣)﹣2=9,
所以c>a>b.
故选:B.
10.【解答】解:∵a⊕b=10a×10b,
∴12⊕3=1012×103=1015.
故选:B.
二.填空题(共6小题)
11.【解答】解:0.000104=1.04×10﹣4,
故答案为:1.04×10﹣4.
12.【解答】解:原式=1+=1,
故答案为:1.
13.【解答】解:22x+y﹣1=22x×2y÷2
=(2x)2×2y÷2
=9×5÷2
=,
故答案为:.
14.【解答】解:原式=,
故答案为:
15.【解答】解:∵2x﹣5y﹣3=0,
∴2x﹣5y=3,
∴4x÷32y=22x÷25y=22x﹣5y=23=8.
故答案为:8.
16.【解答】解:由题意可得:﹣x﹣2dx=﹣2=m﹣1﹣(5m)﹣1,
则﹣=﹣2,
解得:m=﹣.
故答案为:﹣.
三.解答题(共8小题)
17.【解答】解:原式==2.
18.【解答】解:原式=﹣(a﹣b)6+8(a﹣b)6
=7(a﹣b)6
19.【解答】(1)证明:∵2a=4,2b=6,2c=12,
∴2a×2b÷2=4×6÷2=12=2c,
∴a+b﹣1=c,
即a+b﹣c=1;
(2)解:∵2a=4,2b=6,2c=12,
∴22a+b﹣c=(2a)2×2b÷2c
=16×6÷12
=8.
20.【解答】解:a+b=
=×16×(﹣3)+
=﹣5,
∵a是大于﹣6的整数,b是大于﹣1的分数,
∴a=﹣5,b=﹣,
∴(ab)3=64.
21.【解答】解:①由2x+3=1,得x=﹣1,
当x=﹣1时,代数式(2x+3)x+2020=12019=1;
②由2x+3=﹣1,得x=﹣2,
当x=﹣2时,代数式(2x+3)x+2020=(﹣1)2018=1;
③由x+2020=0,得x=﹣2020,
当x=﹣2020时,2x+3=﹣4037≠0
所以(2x+3)x+2020=(﹣4037)0=1.
当x=﹣2020时,代数式(2x+3)x+2020的值为1.
答:当x为﹣1、﹣2、﹣2020时,代数式(2x+3)x+2020的值为1.
22.【解答】解:(1)23=8,2※8=3,
2﹣4=,2※=﹣4,
故答案为:3;﹣4;
(2)设4※5=x,4※6=y,4※30=z,
则4x=5,4y=6,4z=30,
4x×4y=4x+y=30,
∴x+y=z,即4※5+4※6=4※30.
23.【解答】解:(1)∵33=27,
∴(3,27)=3;
∵50=1,
∴(5,1)=0;
∵2﹣2=,
∴(2,)=﹣2;
(2)设(3,4)=x,(3,5)=y,
则3x=4,3y=5,
∴3x+y=3x?3y=20,
∴(3,20)=x+y,
∴(3,4)+(3,5)=(3,20).
24.【解答】解:(1)5﹣2=;(﹣2)﹣2=;
(2)如果2﹣p=,那么p=3;如果a﹣2=,那么a=±4;
(3)由于a、p为整数,
所以当a=9时,p=1;
当a=3时,p=2;
当a=﹣3时,p=2.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
