二叉树[上学期]

(共21张PPT)
数计01计本（1）2001070215
存储结构
顺序存储
链式存储
存储结构的分类
1、顺序存储
2、链式存储
1.1顺序存储图示
1.2顺序存储的二叉树的定义
1.3顺序存储的优缺点
2.1链式存储图示
2.2链式存储的二叉树的定义
1.顺序存储
顺序存储 —— 用一组地址连续的存储单元
来存放二叉树中的各元素。
由于二叉树是非线性结构，所以要想
通过顺序存储把树中结点的逻辑关系反映
出来，就必须将二叉树中的结点按一定的
规律安排在这组存储单元中。
1.顺序存储
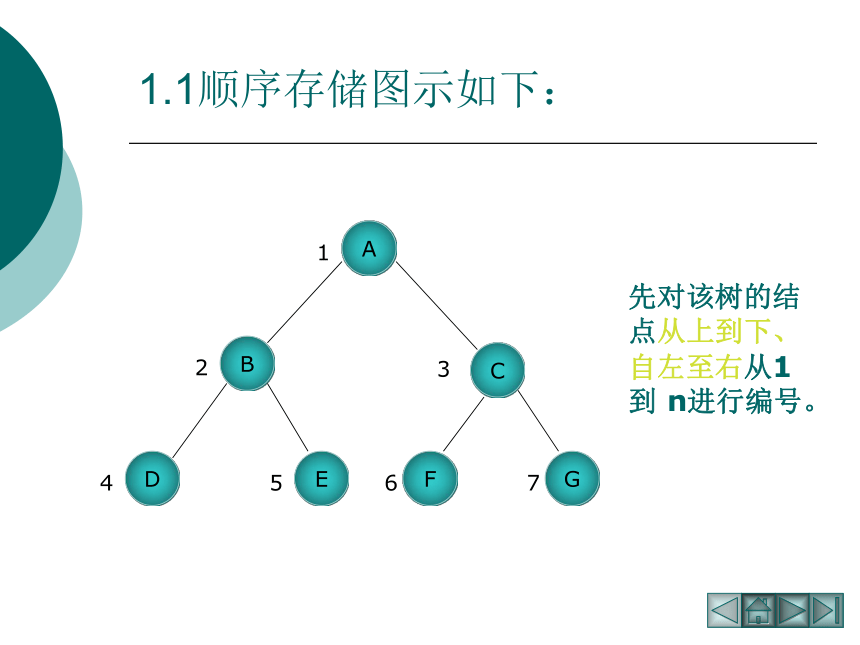
1.1顺序存储图示如下：
A
B
C
D
E
F
先对该树的结点从上到下、自左至右从1到 n进行编号。
1
2
3
4
5
6
G
7
A
B
C
D
E
F
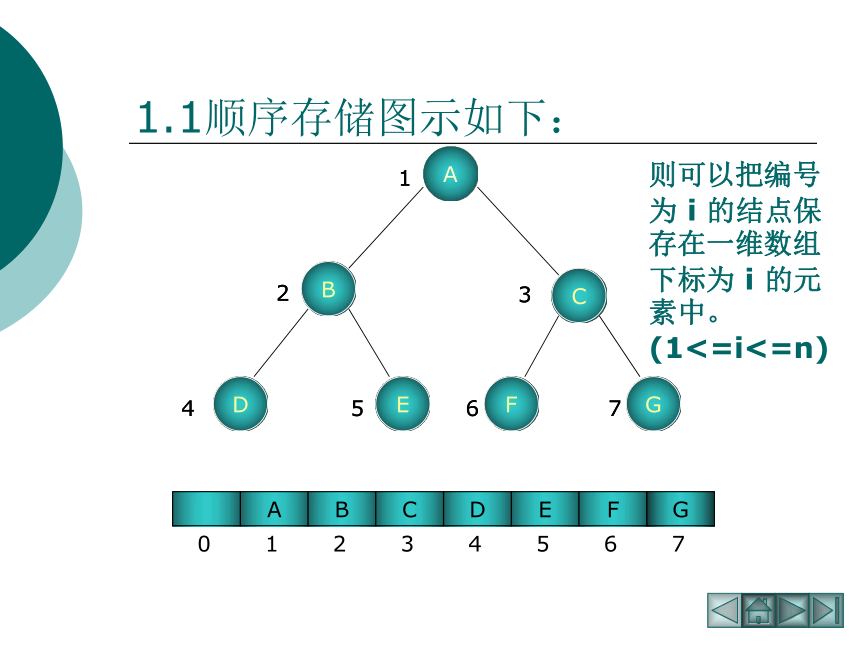
则可以把编号为 i 的结点保存在一维数组下标为 i 的元素中。(1<=i<=n)
1
2
3
4
5
6
G
7
1.1顺序存储图示如下：
2
1
3
4
5
6
7
A
B
C
D
E
F
A
B
C
D
E
F
1
2
3
4
5
6
G
7
0
G
1.2顺序存储的二叉树的定义：
#define N 50
typedef elemtype SQTREE[N]；
1.3顺序存储的优缺点
对于完全二叉树而言，这是一种相当令人
满意的存储方式，因为它没有浪费任何一个存储
单元，不仅存储了结点的数据值，而且任何一个
编号大于1小于n的结点，都可以根据性质5，方
便的找到它的双亲、左子女、右子女，而不需要
增加任何附加存储单元来存放指针。
唯一不方便的就是顺序存储的固有缺点，即
不易实现增、删操作。
1.3顺序存储的优缺点
对于不完全二叉树，如果也按顺序结构储，
则必须假如若干空结点把树“填满”，成为一棵完
全二叉树再进行编号存储。如图
2 链式存储
对于线性表，为了随时进行增、删处理的需要我们要采用链式存储。
二叉树是非线性结构，所以采用链式存储是很自然的，而且在大多数情况下是更为适合的。
2.1 链式存储的图示
二叉树的每一个结点除了数据域外，由于它可能有两个子女，因此，很自然地需要两个分别指向它的左子女和右子女的指针
域，这就是图（b）中的结
点结构：
lchild
data
rchild
(b)含两个指针域的结点结构
parent
lchild
rchild
(a)
2.1 链式存储的图示
在许多应用中，除了需要知道结点的子女信息外，还常常需要知道它的双亲信息，所以，就应增加一个指向双亲的指针域，如
图（c）中的结点结构：
parent
data
rchild
(c)含三个指针域的结点结构
parent
lchild
rchild
(a)
lchild
2.2 链式存储的二叉树的定义
（1）
Typedef struct treenode
{elempty data;

struct treenode *lchild,*rchild;

}TREENODE,*TREENODEEPTR;

2.2 链式存储的二叉树的定义
（2）
Typedef struct treenode
{elempty data;

Struct treenode *lchild,*rchild，*parent;

}TREENODE,*TREENODEEPTR;

（a）二叉链表
A
D
^
G
^
^
B
^
H
^
C
^
E
^
^
F
^
root
图 1
（b）三叉链表
^
A
D
G
^
^
B
^
H
C
E
^
^
F
^
^
^
^
root
图 2
A
B
C
F
1
2
3
4
5
6
A
B
C
F
0 1 2 3 4 5 6 7
7
必须把树补成完全二叉树，浪费存储空间。
图 3
顺序存储的二叉树的缺点：