河北省定州市2019-2020学年八年级上学期期末质量监测数学试题(含答案)
文档属性
| 名称 | 河北省定州市2019-2020学年八年级上学期期末质量监测数学试题(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-22 00:00:00 | ||
图片预览



文档简介
2019-2020学年度第一学期期末质量检测
八年级数学试题
一、选择题:
1.下列图形不是轴对称图形的是( )
2.若分式的值等于0,则的值为( )
1 2
3.纳米是非常小的长度单位,纳米是米,将用科学计数法表示为( )
4.下列算式正确的是( )
5.若,则括号内应填的代数式是( )
6.下列因式分解正确的是( )
7.分式方程的解为( )
8.已知,则代数式的值为( )
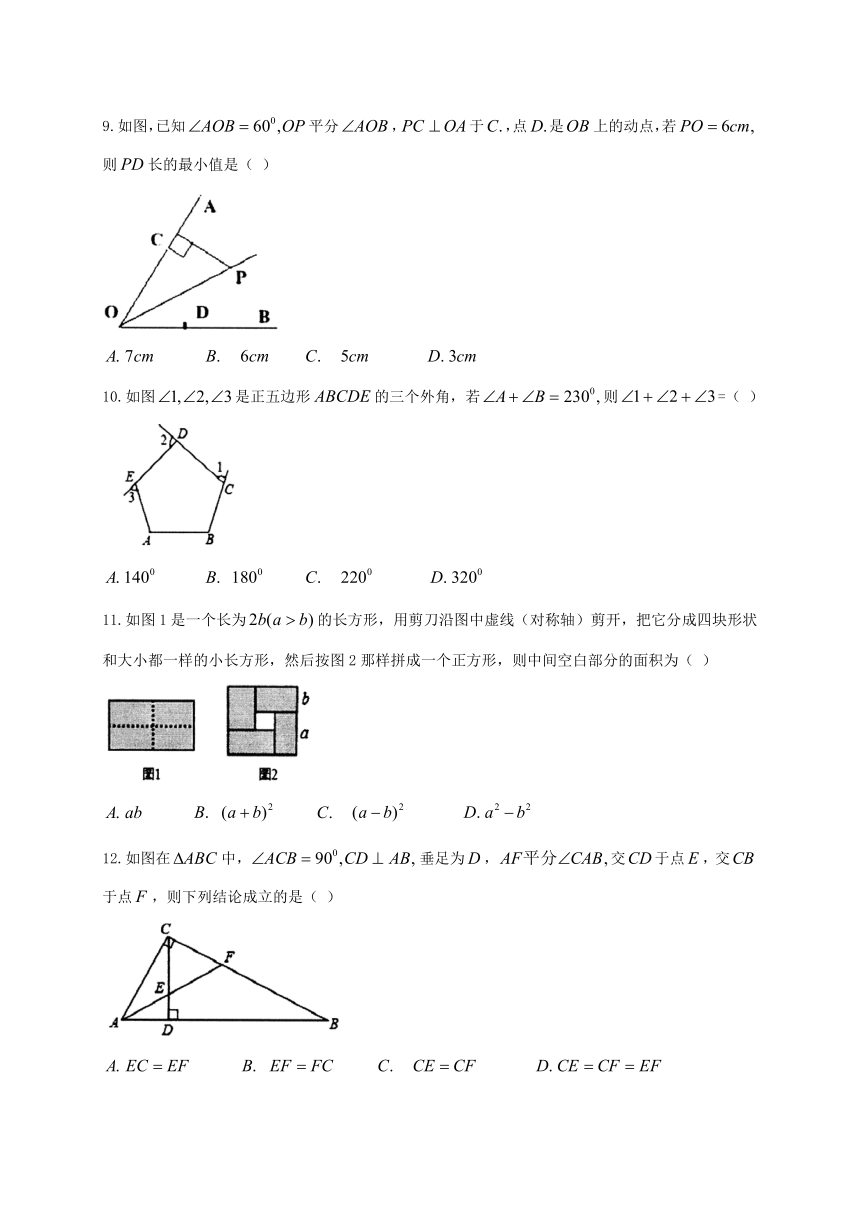
9.如图,已知平分,于,点是上的动点,若则长的最小值是( )
10.如图是正五边形的三个外角,若则=( )
11.如图1是一个长为的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图2那样拼成一个正方形,则中间空白部分的面积为( )
12.如图在中,垂足为,交于点,交于点,则下列结论成立的是( )
二、填空题
的结果是
14.一个等腰三角形一边长为,另一边长为,则这个等腰三角形的周长是
15.若,则的值为
16.已知点和关于轴对称,则的值为
17.如图,在中,分别以点和点为圆心。大于长为半径画弧,两弧相交于点,作直线分别交于点,若的周长为,则为
18..如图,在中,点在上,过点作于点,且,则的度数为 .
三.解答下列各题:
19.计算:
20.因式分解
21⑴解方程
⑵先化简,再求值:
22.请在网格中完成下列问题:
⑴如图1,网格中的与为为轴对称图形,请用所学轴对称的知识作出与的对称轴;
⑵如图2,请在图中作出关于直线成轴对称的图形
23.如图,已知,,与交于,,
求证:⑴
⑵是等腰三角形
24.某超市预测某种饮料会畅销,先用1800元购进一批这种饮料,上市后果然供不应求,又用8100元购进这种饮料,第二批饮料的数量是第一批的3倍,但单价比第一批贵2元.
⑴第二批饮料进货的单价多少元?
⑵若两次进的饮料都按同一价格销售,两批全部售完后,,获利不少于2700元,那么销售单价至少为多少元?
25.⑴分解因式,将结果直接写在横线上:
⑵观察以上三个多项式的系数,有 于是我们猜测,若多项式 是完全平方式,则实数系数一定存在某种关系
①请你用数学式子表示出之间的关系
②解决问题:若多项式是一个完全平方式,求的值.
26.如图,中,,为的中点,绕点旋转,分别与边交于两点
⑴求证:是等腰直角三角形
⑵求证:
⑶若的长为16,求四边形的面积.
八年级数学参考答案
一.选择题
1—6: AABBDB; 7—12:BDDCCC.
二.填空题
13. -1;14. 15或者18;15. 9;16. -1;17. 5;18. 18°。
三.解答题
19.解:⑴原式=15x2y÷5xy-10xy2÷5xy
=3x-2y
⑵原式=4x2+4x+1﹣(4x2﹣25)[来源:学科网ZXXK]
=4x+26;
20.解:⑴原式=ab(a2﹣b2)
=ab(a﹣b)(a+b); [来源:学科网]
⑵原式=x2-7x+x-7+16
=x2-6x+9
=(x-3)2.
21.⑴解:方程两边乘,得
.
解得.
检验:当时,.
∴原分式方程的解为.
⑵解:原式=
=
=
=.
当时,原式=15
22.解:(1)如图1,直线PQ为所作;
(2)如图2,△A′B′C′为所作.
23.证明:⑴∵AC⊥BC,BD⊥AD,
∴∠ADB=∠ACB=90°,
在Rt△ABC和Rt△BAD中,
∵,
∴Rt△ABC≌Rt△BAD(HL),
∴BC=AD,
⑵∵Rt△ABC≌Rt△BAD,
∴∠CAB=∠DBA,
∴OA=OB,
∴△OAB是等腰三角形.
24.解:⑴设第一批饮料进货单价为x元/瓶,
则第二批饮料进货单价为(x+2)元/瓶,
依题意,得:=3×,
解得:x=4,
经检验,x=4是原方程的解,且符合题意.
答:第一批饮料进货单价是4元/瓶.
⑵由⑴可知:第一批购进该种饮料450瓶,
第二批购进该种饮料1350瓶.[来源:Z+xx+k.Com]
设销售单价为y元/瓶,
依题意,得:(450+1350)y﹣1800﹣8100≥2700,
解得:y≥7.
答:销售单价至少为7元/瓶.
25.解:⑴x2+4x+4=(x+2)2,
16x2+24x+9=(4x+3)2,
9x2﹣12x+4=(3x﹣2)2,
⑵①b2=4ac,
②∵多项式x2﹣2(m﹣3)x+(10﹣6m)是一个完全平方式,
∴[﹣2(m﹣3)]2=4×1×(10﹣6m),
m2﹣6m+9=10﹣6m,m2=1,m=±1.
26.⑴证明:∵Rt△ABC中,AB=AC,点D为BC中点,
∴∠C=∠BAD=45°,AD=BD=CD,[来源:学科网ZXXK]
∵∠MDN=90°,
∴∠ADE+∠ADF=∠ADF+∠CDF=90°,
∴∠ADE=∠CDF.
在△AED与△CFD中,
,
∴△AED≌△CFD(ASA),
∴ED=FD.;
⑵由(1)得,AE=CF,
BE+CF=BE+AE=AB=AC
⑶∵△AED≌△CFD,
∴S四边形AEDF=S△ADE+ S△ADF=S△CDF+ S△ADF = S△ADC= AD2.
由已知可得,AD=BD=CD=8
∴S四边形AEDF== AD2.=32.
八年级数学试题
一、选择题:
1.下列图形不是轴对称图形的是( )
2.若分式的值等于0,则的值为( )
1 2
3.纳米是非常小的长度单位,纳米是米,将用科学计数法表示为( )
4.下列算式正确的是( )
5.若,则括号内应填的代数式是( )
6.下列因式分解正确的是( )
7.分式方程的解为( )
8.已知,则代数式的值为( )
9.如图,已知平分,于,点是上的动点,若则长的最小值是( )
10.如图是正五边形的三个外角,若则=( )
11.如图1是一个长为的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图2那样拼成一个正方形,则中间空白部分的面积为( )
12.如图在中,垂足为,交于点,交于点,则下列结论成立的是( )
二、填空题
的结果是
14.一个等腰三角形一边长为,另一边长为,则这个等腰三角形的周长是
15.若,则的值为
16.已知点和关于轴对称,则的值为
17.如图,在中,分别以点和点为圆心。大于长为半径画弧,两弧相交于点,作直线分别交于点,若的周长为,则为
18..如图,在中,点在上,过点作于点,且,则的度数为 .
三.解答下列各题:
19.计算:
20.因式分解
21⑴解方程
⑵先化简,再求值:
22.请在网格中完成下列问题:
⑴如图1,网格中的与为为轴对称图形,请用所学轴对称的知识作出与的对称轴;
⑵如图2,请在图中作出关于直线成轴对称的图形
23.如图,已知,,与交于,,
求证:⑴
⑵是等腰三角形
24.某超市预测某种饮料会畅销,先用1800元购进一批这种饮料,上市后果然供不应求,又用8100元购进这种饮料,第二批饮料的数量是第一批的3倍,但单价比第一批贵2元.
⑴第二批饮料进货的单价多少元?
⑵若两次进的饮料都按同一价格销售,两批全部售完后,,获利不少于2700元,那么销售单价至少为多少元?
25.⑴分解因式,将结果直接写在横线上:
⑵观察以上三个多项式的系数,有 于是我们猜测,若多项式 是完全平方式,则实数系数一定存在某种关系
①请你用数学式子表示出之间的关系
②解决问题:若多项式是一个完全平方式,求的值.
26.如图,中,,为的中点,绕点旋转,分别与边交于两点
⑴求证:是等腰直角三角形
⑵求证:
⑶若的长为16,求四边形的面积.
八年级数学参考答案
一.选择题
1—6: AABBDB; 7—12:BDDCCC.
二.填空题
13. -1;14. 15或者18;15. 9;16. -1;17. 5;18. 18°。
三.解答题
19.解:⑴原式=15x2y÷5xy-10xy2÷5xy
=3x-2y
⑵原式=4x2+4x+1﹣(4x2﹣25)[来源:学科网ZXXK]
=4x+26;
20.解:⑴原式=ab(a2﹣b2)
=ab(a﹣b)(a+b); [来源:学科网]
⑵原式=x2-7x+x-7+16
=x2-6x+9
=(x-3)2.
21.⑴解:方程两边乘,得
.
解得.
检验:当时,.
∴原分式方程的解为.
⑵解:原式=
=
=
=.
当时,原式=15
22.解:(1)如图1,直线PQ为所作;
(2)如图2,△A′B′C′为所作.
23.证明:⑴∵AC⊥BC,BD⊥AD,
∴∠ADB=∠ACB=90°,
在Rt△ABC和Rt△BAD中,
∵,
∴Rt△ABC≌Rt△BAD(HL),
∴BC=AD,
⑵∵Rt△ABC≌Rt△BAD,
∴∠CAB=∠DBA,
∴OA=OB,
∴△OAB是等腰三角形.
24.解:⑴设第一批饮料进货单价为x元/瓶,
则第二批饮料进货单价为(x+2)元/瓶,
依题意,得:=3×,
解得:x=4,
经检验,x=4是原方程的解,且符合题意.
答:第一批饮料进货单价是4元/瓶.
⑵由⑴可知:第一批购进该种饮料450瓶,
第二批购进该种饮料1350瓶.[来源:Z+xx+k.Com]
设销售单价为y元/瓶,
依题意,得:(450+1350)y﹣1800﹣8100≥2700,
解得:y≥7.
答:销售单价至少为7元/瓶.
25.解:⑴x2+4x+4=(x+2)2,
16x2+24x+9=(4x+3)2,
9x2﹣12x+4=(3x﹣2)2,
⑵①b2=4ac,
②∵多项式x2﹣2(m﹣3)x+(10﹣6m)是一个完全平方式,
∴[﹣2(m﹣3)]2=4×1×(10﹣6m),
m2﹣6m+9=10﹣6m,m2=1,m=±1.
26.⑴证明:∵Rt△ABC中,AB=AC,点D为BC中点,
∴∠C=∠BAD=45°,AD=BD=CD,[来源:学科网ZXXK]
∵∠MDN=90°,
∴∠ADE+∠ADF=∠ADF+∠CDF=90°,
∴∠ADE=∠CDF.
在△AED与△CFD中,
,
∴△AED≌△CFD(ASA),
∴ED=FD.;
⑵由(1)得,AE=CF,
BE+CF=BE+AE=AB=AC
⑶∵△AED≌△CFD,
∴S四边形AEDF=S△ADE+ S△ADF=S△CDF+ S△ADF = S△ADC= AD2.
由已知可得,AD=BD=CD=8
∴S四边形AEDF== AD2.=32.
同课章节目录
