2020春湘教版八下数学2.1多边形教学课件(24张ppt)
文档属性
| 名称 | 2020春湘教版八下数学2.1多边形教学课件(24张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 493.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-23 00:00:00 | ||
图片预览







文档简介
课件24张PPT。教学课件
数学 八年级下册 湘教版
第2章 四边形
2.1 多边形你能从图中找出一些由线段首尾相连所组成的图形吗?
多边形
在平面内,由一些线段首尾顺次相接组成的封闭图形叫作多边形.
组成多边形的各条线段叫作多边形的边.
相邻两条边的公共端点叫作多边形的顶点.
连接不相邻的两个顶点的线段叫作多边形的对角线.
相邻两边组成的角叫作多边形的内角,简称多边形的角.
如图,AB是边,E是顶点,BD是对角线,∠A是内角.多边形根据边数可以分为三角形,四边形,五边形,……在平面内,边相等、角也相等的多边形叫作正多边形.三角形的内角和等于180°,四边形的内角和是多少度呢?
如图,四边形ABCD的一条对角线AC把它分成两个三角形,因此四边形的内角和等于这两个三角形的内角和,即180°×2=360°.
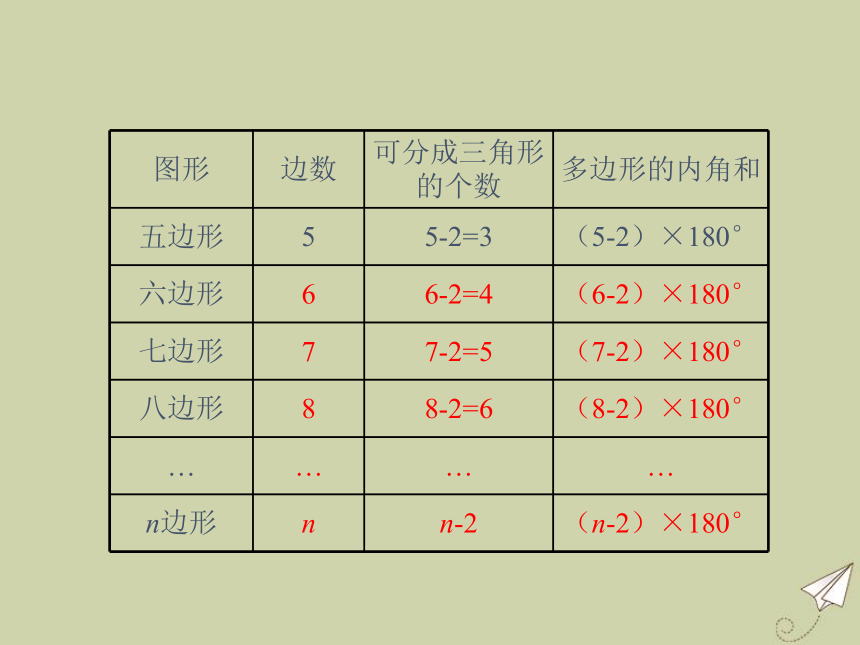
新知探究 1 在下列各个多边形中,任取一个顶点,通过该顶点画出所有对角线,并完成表格.
n边形的内角和等于(n-2)·180°.如图,n边形共有n个顶点A1,A2,A3,…,An,与顶点A1不相邻的点有(n-3)个,因此从顶点A1发出(n-3)条对角线,n边形被分成了(n-2)个三角形.n边形的内角和等于(n-2)个三角形的内角和,即(n-2)·180°.
你还可以用其他方法探究n边形的内角和公式吗?如图,在n边形内任取一点O,与多边形各顶点连接,把n边形分成n个三角形,用n个三角形的内角和n ·180°减去中心的周角360°,得n边形的内角和为(n -2)·180°.
【例1】(1)十边形的内角和是多少度?
(2)一个多边形的内角和等于1980°,它是几边形?解:(1)十边形的内角和是
(10-2)×180°=1440°.
(2)设这个多边形的边数为n,则
(n-2)×180°=1980°,
解得 n=13.
所以这是一个十三边形.1.(1)正十二边形的每一个内角是多少度?
(2)一个多边形的内角和等于1800°,它是几边形?答案:(1)150°.
(2)十二边形.2.过多边形某个顶点的所有对角线,将这个多边形分成10个三角形,那么这个多边形是几边形?答案:十二边形.外角 F多边形的内角的一边与另一边的反向延长线所组成的角叫作这个多边形的一个外角.如图,∠EDF是五边形ABCDE的一个外角.
在多边形的每个顶点处取一个外角,它们的和叫作这个多边形的外角和.如图,在四边形ABCD的每一个顶点处取一个外角,如∠1,∠2,∠3,∠4.
∵∠1+∠DAB=180°,∠2+∠ABC=
180°,∠3+∠BCD=180°,∠4+∠ADC=
180°,∠DAB+∠ABC+∠BCD+∠ADC=
360°,∴∠1+∠2+∠3+∠4=4×180°-
360°=360°.∴四边形的外角和为360°.我们已经知道三角形的外角和为360°,那么四边形的外角和为多少度呢?新知探究 2三角形的外角和是360°,四边形的外角和是360°,n边形(n为不小于3的任意整数)的外角和都是360°吗?n边形的外角和与边数有关系吗?
n边形的外角和与边数没有关系.任意多边形的外角和等于360°.类似于求四边形外角和的思路,在n边形的每一个顶点处取一个外角,其中每一个外角与它相邻的内角之和为180°.因此,这n个外角与它相邻的内角之和加起来是n·180°,将这个总和减去n边形的内角和(n-2)·180°所得的差即为n边形的外角和.
【例2】一个多边形的内角和等于它的外角和的5倍,它是几边形?解:设多边形的边数为n,则它的内角和为(n-2)·180°.
由题意,得 (n-2)·180°=360°×5,
解得n=12.
因此这个多边形是十二边形.三角形具有稳定性,那么四边形呢?用4根木条钉成如图的木框,随意扭转四边形的边,它的形状会发生变化吗?
我们可以发现,四边形的边长不变,但它的形状改变了,这说明四边形具有不稳定性.
在实际生活中,我们经常利用四边形的不稳定性,如图中的电动伸缩门与升降器.有时候我们也要克服四边形的不稳定性,如图中的栅栏中间加钉木条,构成三角形,这是利用了三角形的稳定性.
1.一个多边形的每一个外角都等于45°,这个多边形是几边形?它的每一个内角是多少度?答案:这个多边形是八边形,每一个内角均为135°.2.如图,求图中x的值.答案:x=60.3.请举出日常生活中利用四边形不稳定性的一些例子.解:略.通过本节课,你有什么收获?
你还存在哪些疑问,和同伴交流.
数学 八年级下册 湘教版
第2章 四边形
2.1 多边形你能从图中找出一些由线段首尾相连所组成的图形吗?
多边形
在平面内,由一些线段首尾顺次相接组成的封闭图形叫作多边形.
组成多边形的各条线段叫作多边形的边.
相邻两条边的公共端点叫作多边形的顶点.
连接不相邻的两个顶点的线段叫作多边形的对角线.
相邻两边组成的角叫作多边形的内角,简称多边形的角.
如图,AB是边,E是顶点,BD是对角线,∠A是内角.多边形根据边数可以分为三角形,四边形,五边形,……在平面内,边相等、角也相等的多边形叫作正多边形.三角形的内角和等于180°,四边形的内角和是多少度呢?
如图,四边形ABCD的一条对角线AC把它分成两个三角形,因此四边形的内角和等于这两个三角形的内角和,即180°×2=360°.
新知探究 1 在下列各个多边形中,任取一个顶点,通过该顶点画出所有对角线,并完成表格.
n边形的内角和等于(n-2)·180°.如图,n边形共有n个顶点A1,A2,A3,…,An,与顶点A1不相邻的点有(n-3)个,因此从顶点A1发出(n-3)条对角线,n边形被分成了(n-2)个三角形.n边形的内角和等于(n-2)个三角形的内角和,即(n-2)·180°.
你还可以用其他方法探究n边形的内角和公式吗?如图,在n边形内任取一点O,与多边形各顶点连接,把n边形分成n个三角形,用n个三角形的内角和n ·180°减去中心的周角360°,得n边形的内角和为(n -2)·180°.
【例1】(1)十边形的内角和是多少度?
(2)一个多边形的内角和等于1980°,它是几边形?解:(1)十边形的内角和是
(10-2)×180°=1440°.
(2)设这个多边形的边数为n,则
(n-2)×180°=1980°,
解得 n=13.
所以这是一个十三边形.1.(1)正十二边形的每一个内角是多少度?
(2)一个多边形的内角和等于1800°,它是几边形?答案:(1)150°.
(2)十二边形.2.过多边形某个顶点的所有对角线,将这个多边形分成10个三角形,那么这个多边形是几边形?答案:十二边形.外角 F多边形的内角的一边与另一边的反向延长线所组成的角叫作这个多边形的一个外角.如图,∠EDF是五边形ABCDE的一个外角.
在多边形的每个顶点处取一个外角,它们的和叫作这个多边形的外角和.如图,在四边形ABCD的每一个顶点处取一个外角,如∠1,∠2,∠3,∠4.
∵∠1+∠DAB=180°,∠2+∠ABC=
180°,∠3+∠BCD=180°,∠4+∠ADC=
180°,∠DAB+∠ABC+∠BCD+∠ADC=
360°,∴∠1+∠2+∠3+∠4=4×180°-
360°=360°.∴四边形的外角和为360°.我们已经知道三角形的外角和为360°,那么四边形的外角和为多少度呢?新知探究 2三角形的外角和是360°,四边形的外角和是360°,n边形(n为不小于3的任意整数)的外角和都是360°吗?n边形的外角和与边数有关系吗?
n边形的外角和与边数没有关系.任意多边形的外角和等于360°.类似于求四边形外角和的思路,在n边形的每一个顶点处取一个外角,其中每一个外角与它相邻的内角之和为180°.因此,这n个外角与它相邻的内角之和加起来是n·180°,将这个总和减去n边形的内角和(n-2)·180°所得的差即为n边形的外角和.
【例2】一个多边形的内角和等于它的外角和的5倍,它是几边形?解:设多边形的边数为n,则它的内角和为(n-2)·180°.
由题意,得 (n-2)·180°=360°×5,
解得n=12.
因此这个多边形是十二边形.三角形具有稳定性,那么四边形呢?用4根木条钉成如图的木框,随意扭转四边形的边,它的形状会发生变化吗?
我们可以发现,四边形的边长不变,但它的形状改变了,这说明四边形具有不稳定性.
在实际生活中,我们经常利用四边形的不稳定性,如图中的电动伸缩门与升降器.有时候我们也要克服四边形的不稳定性,如图中的栅栏中间加钉木条,构成三角形,这是利用了三角形的稳定性.
1.一个多边形的每一个外角都等于45°,这个多边形是几边形?它的每一个内角是多少度?答案:这个多边形是八边形,每一个内角均为135°.2.如图,求图中x的值.答案:x=60.3.请举出日常生活中利用四边形不稳定性的一些例子.解:略.通过本节课,你有什么收获?
你还存在哪些疑问,和同伴交流.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
